repeated measures design on:
[Wikipedia]
[Google]
[Amazon]
Repeated measures design is a
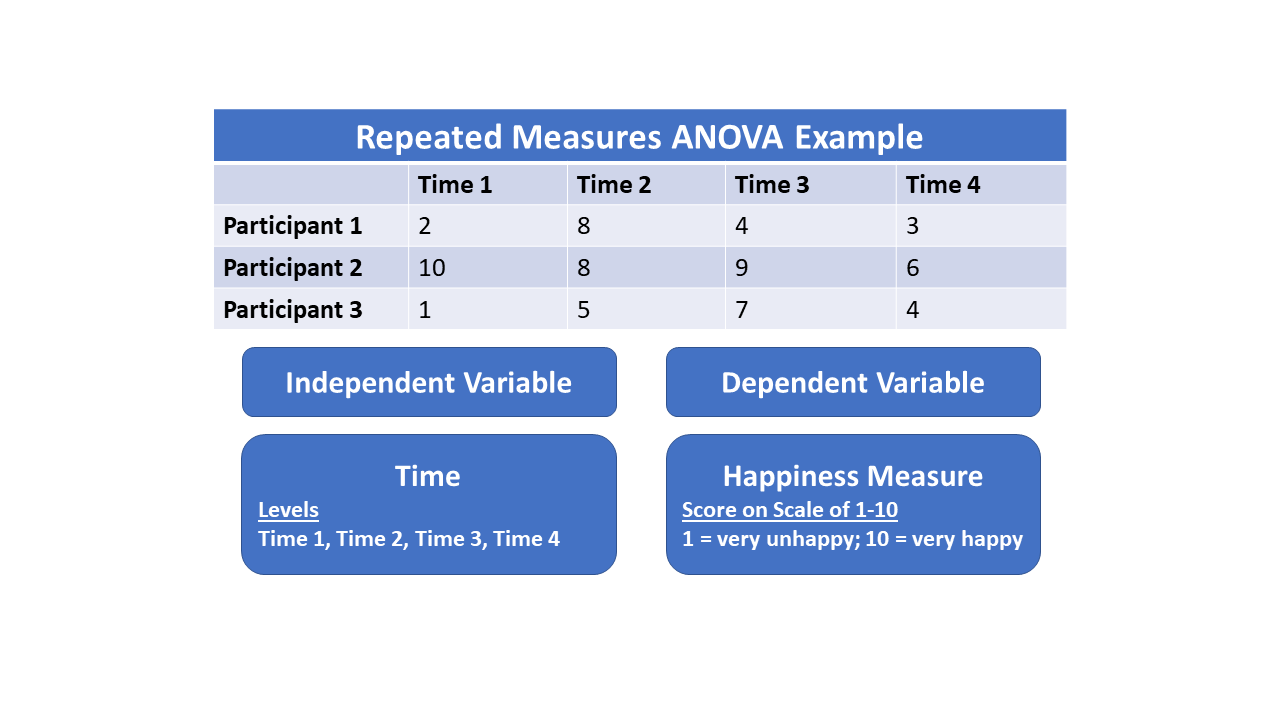 Repeated measures analysis of variance (rANOVA) is a commonly used statistical approach to repeated measure designs. With such designs, the repeated-measure factor (the qualitative independent variable) is the within-subjects factor, while the dependent quantitative variable on which each participant is measured is the dependent variable.
Repeated measures analysis of variance (rANOVA) is a commonly used statistical approach to repeated measure designs. With such designs, the repeated-measure factor (the qualitative independent variable) is the within-subjects factor, while the dependent quantitative variable on which each participant is measured is the dependent variable.
Examples of all ANOVA and ANCOVA models with up to three treatment factors, including randomized block, split plot, repeated measures, and Latin squares, and their analysis in R
(University of Southampton) {{Statistics, collection, state=collapsed Design of experiments Science experiments Analysis of variance Statistical reliability
research design
Research design refers to the overall strategy utilized to answer research questions. A research design typically outlines the theories and models underlying a project; the research question(s) of a project; a strategy for gathering data and info ...
that involves multiple measures of the same variable taken on the same or matched subjects either under different conditions or over two or more time periods. For instance, repeated measurements are collected in a longitudinal study
A longitudinal study (or longitudinal survey, or panel study) is a research design that involves repeated observations of the same variables (e.g., people) over long periods of time (i.e., uses longitudinal data). It is often a type of observationa ...
in which change over time is assessed.
Crossover studies
A popular repeated-measures design is the crossover study. A crossover study is alongitudinal study
A longitudinal study (or longitudinal survey, or panel study) is a research design that involves repeated observations of the same variables (e.g., people) over long periods of time (i.e., uses longitudinal data). It is often a type of observationa ...
in which subjects receive a sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is cal ...
of different treatments (or exposures). While crossover studies can be observational studies
In fields such as epidemiology, social sciences, psychology and statistics, an observational study draws inferences from a sample to a population where the independent variable is not under the control of the researcher because of ethical conc ...
, many important crossover studies are controlled experiments. Crossover designs are common for experiments in many scientific
Science is a systematic discipline that builds and organises knowledge in the form of testable hypotheses and predictions about the universe. Modern science is typically divided into twoor threemajor branches: the natural sciences, which stu ...
disciplines, for example psychology
Psychology is the scientific study of mind and behavior. Its subject matter includes the behavior of humans and nonhumans, both consciousness, conscious and Unconscious mind, unconscious phenomena, and mental processes such as thoughts, feel ...
, education
Education is the transmission of knowledge and skills and the development of character traits. Formal education occurs within a structured institutional framework, such as public schools, following a curriculum. Non-formal education als ...
, pharmaceutical science
Pharmacy is the science and practice of discovering, producing, preparing, dispensing, reviewing and monitoring medications, aiming to ensure the safe, effective, and affordable use of medication, medicines. It is a miscellaneous science as it ...
, and health care
Health care, or healthcare, is the improvement or maintenance of health via the preventive healthcare, prevention, diagnosis, therapy, treatment, wikt:amelioration, amelioration or cure of disease, illness, injury, and other disability, physic ...
, especially medicine.
Randomized, controlled, crossover experiments are especially important in health care. In a randomized clinical trial
Clinical trials are prospective biomedical or behavioral research studies on human subject research, human participants designed to answer specific questions about biomedical or behavioral interventions, including new treatments (such as novel v ...
, the subjects are randomly assigned treatments. When such a trial is a repeated measures design, the subjects are randomly assigned to a sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is cal ...
of treatments. A crossover clinical trial is a repeated-measures design in which each patient is randomly assigned to a sequence of treatments, including at least two treatments (of which one may be a standard treatment or a placebo
A placebo ( ) can be roughly defined as a sham medical treatment. Common placebos include inert tablets (like sugar pills), inert injections (like saline), sham surgery, and other procedures.
Placebos are used in randomized clinical trials ...
): Thus each patient crosses over from one treatment to another.
Nearly all crossover designs have "balance", which means that all subjects should receive the same number of treatments and that all subjects participate for the same number of periods. In most crossover trials, each subject receives all treatments.
However, many repeated-measures designs are not crossovers: the longitudinal study of the sequential effects of repeated ''treatments'' need not use any " crossover", for example (Vonesh & Chinchilli; Jones & Kenward).
Uses
* Limited number of participants—The repeated measure design reduces the variance of estimates of treatment-effects, allowing statistical inference to be made with fewer subjects. * Efficiency—Repeated measure designs allow many experiments to be completed more quickly, as fewer groups need to be trained to complete an entire experiment. For example, experiments in which each condition takes only a few minutes, whereas the training to complete the tasks take as much, if not more time. * Longitudinal analysis—Repeated measure designs allow researchers to monitor how participants change over time, both long- and short-term situations.Order effects
Order effect
Order, ORDER or Orders may refer to:
* A socio-political or established or existing order, e.g. World order, Ancien Regime, Pax Britannica
* Categorization, the process in which ideas and objects are recognized, differentiated, and understood
* ...
s may occur when a participant in an experiment is able to perform a task and then perform it again. Examples of order effects include performance improvement or decline in performance, which may be due to learning effects, boredom or fatigue. The impact of order effects may be smaller in long-term longitudinal studies or by counterbalancing using a crossover design.
Counterbalancing
In this technique, two groups each perform the same tasks or experience the same conditions, but in reverse order. With two tasks or conditions, four groups are formed. Counterbalancing attempts to take account of two important sources of systematic variation in this type of design: practice and boredom effects. Both might otherwise lead to different performance of participants due to familiarity with or tiredness to the treatments.Limitations
It may not be possible for each participant to be in all conditions of the experiment (i.e. time constraints, location of experiment, etc.). Severely diseased subjects tend to drop out of longitudinal studies, potentially biasing the results. In these cases mixed effects models would be preferable as they can deal with missing values. Mean regression may affect conditions with significant repetitions. Maturation may affect studies that extend over time. Events outside the experiment may change the response between repetitions.Repeated measures ANOVA
 Repeated measures analysis of variance (rANOVA) is a commonly used statistical approach to repeated measure designs. With such designs, the repeated-measure factor (the qualitative independent variable) is the within-subjects factor, while the dependent quantitative variable on which each participant is measured is the dependent variable.
Repeated measures analysis of variance (rANOVA) is a commonly used statistical approach to repeated measure designs. With such designs, the repeated-measure factor (the qualitative independent variable) is the within-subjects factor, while the dependent quantitative variable on which each participant is measured is the dependent variable.
Partitioning of error
One of the greatest advantages to rANOVA, as is the case with repeated measures designs in general, is the ability to partition out variability due to individual differences. Consider the general structure of the F-statistic: : F = MSTreatment / MSError = (SSTreatment/dfTreatment)/(SSError/dfError) In a between-subjects design there is an element of variance due to individual difference that is combined with the treatment and error terms: : SSTotal = SSTreatment + SSError : dfTotal = ''n'' − 1 In a repeated measures design it is possible to partition subject variability from the treatment and error terms. In such a case, variability can be broken down into between-treatments variability (or within-subjects effects, excluding individual differences) and within-treatments variability. The within-treatments variability can be further partitioned into between-subjects variability (individual differences) and error (excluding the individual differences): : SSTotal = SSTreatment (excluding individual difference) + SSSubjects + SSError : dfTotal = dfTreatment (within subjects) + dfbetween subjects + dferror = (''k'' − 1) + (''s'' − 1) + ((''k - 1'')(''s'' − 1)) = ''ks -1= n-1,'' where ''k'' is the number of time levels and ''s'' is the number of subjects. In reference to the general structure of the F-statistic, it is clear that by partitioning out the between-subjects variability, the F-value will increase because the sum of squares error term will be smaller resulting in a smaller MSError. It is noteworthy that partitioning variability reduces degrees of freedom from the F-test, therefore the between-subjects variability must be significant enough to offset the loss in degrees of freedom. If between-subjects variability is small this process may actually reduce the F-value.Assumptions
As with all statistical analyses, specific assumptions should be met to justify the use of this test. Violations can moderately to severely affect results and often lead to an inflation of type 1 error. With the rANOVA, standard univariate and multivariate assumptions apply. The univariate assumptions are: * Normality—For each level of the within-subjects factor, the dependent variable must have anormal distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
f(x) = \frac ...
.
* Sphericity
Sphericity is a measure of how closely the shape of a physical object resembles that of a perfect sphere. For example, the sphericity of the ball (bearing), balls inside a ball bearing determines the quality (business), quality of the bearing, ...
—Difference scores computed between two levels of a within-subjects factor must have the same variance for the comparison of any two levels. (This assumption only applies if there are more than 2 levels of the independent variable.)
* Randomness—Cases should be derived from a random sample, and scores from different participants should be independent of each other.
The rANOVA also requires that certain multivariate assumptions be met, because a multivariate test is conducted on difference scores. These assumptions include:
* Multivariate normality—The difference scores are multivariately normally distributed in the population.
* Randomness—Individual cases should be derived from a random sample, and the difference scores for each participant are independent from those of another participant.
F test
As with other analysis of variance tests, the rANOVA makes use of an F statistic to determine significance. Depending on the number of within-subjects factors and assumption violations, it is necessary to select the most appropriate of three tests: * Standard Univariate ANOVA F test—This test is commonly used given only two levels of the within-subjects factor (i.e. time point 1 and time point 2). This test is not recommended given more than 2 levels of the within-subjects factor because the assumption of sphericity is commonly violated in such cases. * Alternative Univariate test—These tests account for violations to the assumption of sphericity, and can be used when the within-subjects factor exceeds 2 levels. The F statistic is the same as in the Standard Univariate ANOVA F test, but is associated with a more accurate p-value. This correction is done by adjusting the degrees of freedom downward for determining the critical F value. Two corrections are commonly used: the Greenhouse–Geisser correction and the Huynh–Feldt correction. The Greenhouse–Geisser correction is more conservative, but addresses a common issue of increasing variability over time in a repeated-measures design. The Huynh–Feldt correction is less conservative, but does not address issues of increasing variability. It has been suggested that lower Huynh–Feldt be used with smaller departures from sphericity, while Greenhouse–Geisser be used when the departures are large. * Multivariate Test—This test does not assume sphericity, but is also highly conservative.Effect size
One of the most commonly reported effect size statistics for rANOVA is partial eta-squared (ηp2). It is also common to use the multivariate η2 when the assumption of sphericity has been violated, and the multivariate test statistic is reported. A third effect size statistic that is reported is the generalized η2, which is comparable to ηp2 in a one-way repeated measures ANOVA. It has been shown to be a better estimate of effect size with other within-subjects tests.Cautions
rANOVA is not always the best statistical analysis for repeated measure designs. The rANOVA is vulnerable to effects from missing values, imputation, unequivalent time points between subjects and violations of sphericity. These issues can result in sampling bias and inflated rates of Type I error. In such cases it may be better to consider use of a linear mixed model.See also
Notes
References
Design and analysis of experiments
* *Exploration of longitudinal data
* * * * * * * * * * (Comprehensive treatment of theory and practice) * Conaway, M. (1999, October 11). Repeated Measures Design. Retrieved February 18, 2008, from http://biostat.mc.vanderbilt.edu/twiki/pub/Main/ClinStat/repmeas.PDF * Minke, A. (1997, January). Conducting Repeated Measures Analyses: Experimental Design Considerations. Retrieved February 18, 2008, from Ericae.net: http://ericae.net/ft/tamu/Rm.htm * Shaughnessy, J. J. (2006). Research Methods in Psychology. New York: McGraw-Hill.External links
Examples of all ANOVA and ANCOVA models with up to three treatment factors, including randomized block, split plot, repeated measures, and Latin squares, and their analysis in R
(University of Southampton) {{Statistics, collection, state=collapsed Design of experiments Science experiments Analysis of variance Statistical reliability