Rayleigh–Kuo Criterion

The Rayleigh–Kuo criterion (sometimes called the Kuo criterion) is a stability condition for a fluid. This criterion determines whether or not a barotropic instability can occur, leading to the presence of vortices (like eddies and storms). The Kuo criterion states that for barotropic instability to occur, the gradient of the absolute vorticity must change its sign at some point within the boundaries of the current. Note that this criterion is a necessary condition, so if it does not hold it is not possible for a barotropic instability to form. But it is not a sufficient condition, meaning that if the criterion is met, this does not automatically mean that the fluid is unstable. If the criterion is not met, it is certain that the flow is stable.

This criterion was formulated by Hsiao-Lan Kuo and is based on Rayleigh's equation named after the Lord Rayleigh who first introduced this equation in fluid dynamics.

Barotropic instability

Vortices like eddies are created by instabilities in a flow. When there are instabilities within the mean flow, energy can be transferred from the mean flow to the small perturbations which can then grow. In a barotropic fluid the density is a function of only the pressure and not the temperature (in contrast to a baroclinic fluid, where the density is a function of both the pressure and temperature). This means that surfaces of constant density ( isopycnals) are also surfaces of constant pressure ( isobars). Barotropic instability can form in different ways. 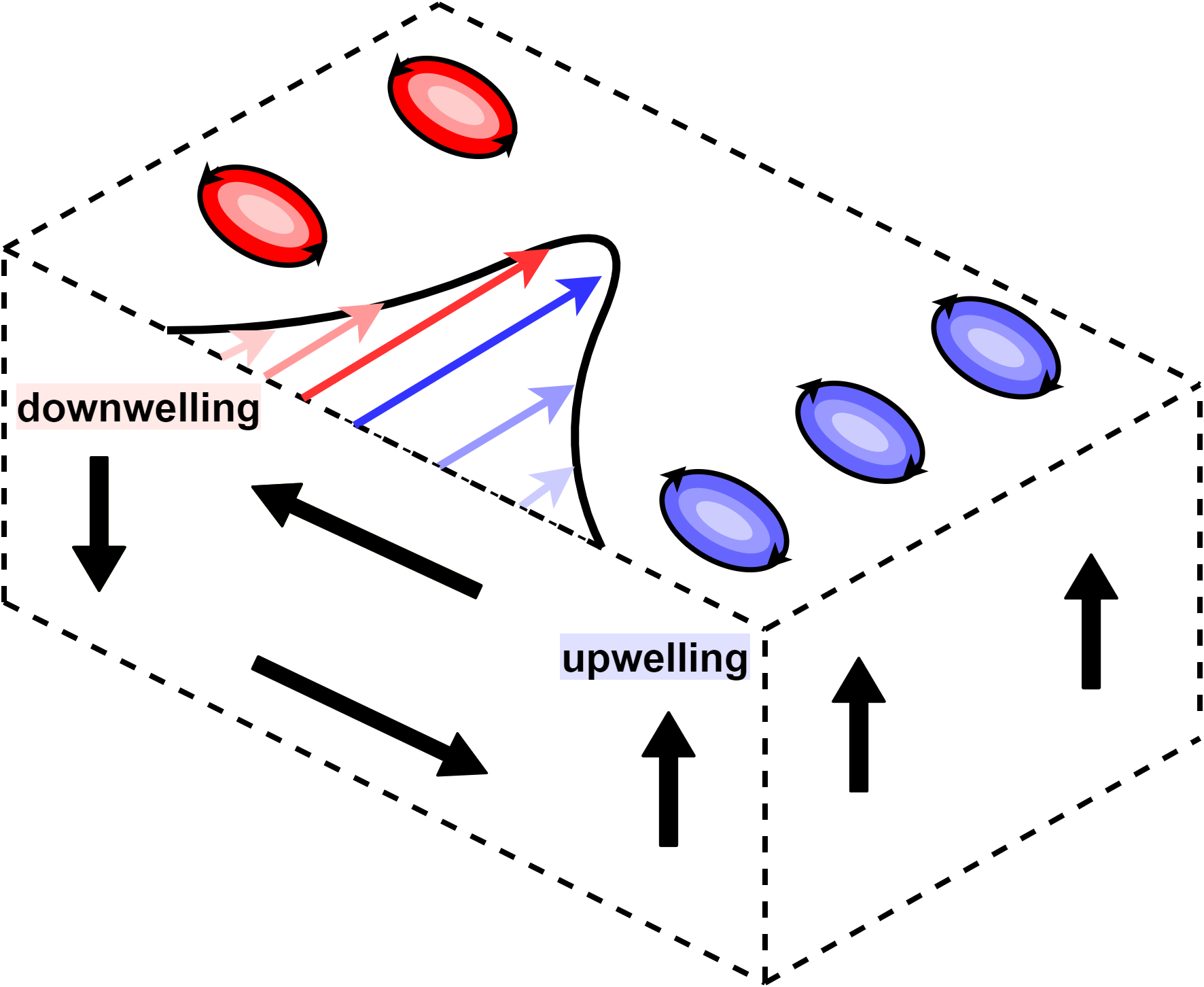Two examples are; when there is an interaction between the fluid flow and the bathymetry or topography of the domain; when there are frontal instabilities (may also lead to baroclinic instabilities). These instabilities are not dependent on the density and might even occur when the density of the fluid is constant. Instead, most of the instabilities are caused by a shear on the flow as can be seen in Figure 1. This shear in the velocity field induces a vertical and horizontal vorticity within the flow. As a result, there is upwelling on the right of the flow and downwelling on the left. This situation might lead to a barotropic unstable flow. The eddies that form alternatingly on both sides of the flow are part of this instability.

Another way to achieve this instability is to displace the Rossby waves in the horizontal direction (see Figure 2). This leads to a transfer of kinetic energy (not potential energy) from the mean flow towards the small perturbations (the eddies). The Rayleigh–Kuo criterion states that the gradient of the absolute vorticity should change sign within the domain. In the example of the shear induced eddies on the right, this means that the second derivative of the flow in the cross-flow direction, should be zero somewhere. This happens in the centre of the eddies, where the acceleration of the flow perpendicular to the flow changes direction.

Examples

The presence of these instabilities in a rotating fluid have been observed in laboratory experiments. The settings of the experiment were based on the conditions in the Gulf Stream and showed that within the ocean currents such as the Gulf Stream, it is possible for barotropic instabilities to occur. But barotropic instabilities were also observed in other Western Boundary Currents (WBC). In the Agulhas current, the barotropic instability leads to ring shedding. The Agulhas current retroflects (turns back) near the coast of South Africa. At this same location, some anti-cyclonic rings of warm water escape from the mean current and travel along the coast of Africa. The formation of these rings is a manifestation of a barotropic instability.

Derivation

The derivation of the Rayleigh–Kuo criterion was first written down by Hsiao-Lan Kuo in his paper called '''dynamic instability of two-dimensional nondivergent flow in a barotropic atmosphere from 1949''.'' This derivation is repeated and simplified below.

First, the assumptions made by Hsiao-Lan Kuo are discussed. Second, the Rayleigh equation is derived in order continue to derive the Rayleigh–Kuo criterion. By integrating this equation and filling in the boundary conditions, the Kuo criterion can be obtained.

Assumptions

In order to derive the Rayleigh–Kuo criterion, some assumptions are made on the fluids properties. We consider a nondivergent, two-dimensional barotropic fluid. The fluid has a mean zonal flow direction which can vary in the meridional direction. On this mean flow, some small perturbations are imposed in both the zonal and meridional direction: $u(y,t) = U(y) + u^*(y,t)$ and $v = v^*$. The perturbations need to be small in order to linearize the vorticity equation. Vertical motion and divergence and convergence of the fluid are neglected. When taking into account these factors, a similar result would have been obtained with only a small shift in the position of the criterion within the velocity profile.

The derivation of the Kuo criterion will be done within the domain L= ,y /math>. On the northern and southern boundary of this domain, the meridional fluid is zero.

Rayleigh Equation

Barotropic vorticity equation

To derive the Rayleigh equation for a barotropic fluid, the barotropic vorticity equation is used. This equation assumes that the absolute vorticity is conserved: $\frac = 0$ here, $\frac$ is the material derivative. The absolute vorticity is the relative vorticity plus the planetary vorticity: $\zeta_a = \zeta + f$. The relative vorticity, $\zeta$, is the rotation of the fluid with respect to the Earth. The planetary vorticity (also called Coriolis frequency),$f$, is the vorticity of a parcel induced by the rotation of the Earth. When applying the beta-plane approximation for the planetary vorticity, the conservation of absolute vorticity looks like:

$\frac = \frac\left(\zeta + \beta y \right) = 0$
The relative vorticity is defined as $\zeta = \frac - \frac.$ Since the flow field consist of a mean flow with small perturbations, it can be written as $\zeta = \overline + \zeta^*$ with $\overline = -\frac$ and $\zeta^* = \frac - \frac.$ This formulation is used in the vorticity equation:

$\begin 0 &= \frac\left(\zeta + \beta y\right) \\ 0 &= \frac\left(\zeta ' + \overline + \beta y\right) \\ 0 &= \left( \frac + u\frac + v\frac \right) \left(\zeta^* - \frac + \beta y \right) \end$Here, $u$ and $v$ are the zonal and meridional components of the flow and $\zeta'$ is the relative vorticity induced by the perturbations on the flow ($u'$ and $v'$). $U$ is the mean zonal flow and $\beta$ is derivative of the planetary vorticity $f$ with respect to $y$ .

Linearization

A zonal mean flow with small perturbations was assumed, $u = U+ u^*$, and a meridional flow with a zero mean, $v = v^*$. Since it was assumed that the perturbations are small, a linearization can be performed on the barotropic vorticity equation above, ignoring all the non-linear terms (terms where two or more small variables, i.e. $u^*, v^*, \zeta^*$, are multiplied with one another). Also the derivative of $u$ in the zonal direction, the time derivative of the mean flow $U$ and the time derivative of $\beta y$ are zero. This results in a simplified equation:

$\begin 0 &= \left( \frac + U\frac\right)\zeta' - v'\frac\frac + v'\frac \left(\beta y\right)\\ 0 &= \left( \frac + U\frac \right)\zeta' + v' \left( \beta - \frac\right). \end$

With $\zeta'$ as defined above ($\zeta^* = \frac - \frac$) and $u^*$ and $v^*$ the small perturbations in the zonal and meridional components of the flow.

Stream function

To find the solution to the linearized equation, a stream function was introduced by Lord Rayleigh for the perturbations of the flow velocity:

$u^* = \frac, \;\;\;\; v^* = \frac.$These new definitions of the stream function are used to rewrite the linearized barotropic vorticity equation.
$\begin 0 &= \left(\frac + U\frac\right) \left(\frac - \frac\right) + v^*\left(\beta - \frac\right)\\ 0 &= \left(\frac + U\frac\right) \left(-\frac - \frac\right) - \frac\left(\beta - U''\right)\\ 0 &= \left(\frac + U\frac\right) \nabla^2 \psi + \frac\left(\beta - U''\right) \end$Here, $U''$ is the second derivative of $U$ with respect to $y$ $(U'' = \frac)$. To solve this equation for the stream function, a wave-like solution was proposed by Rayleigh which reads $\psi(x,y,t) = \Psi(y)e^$. The amplitude $\Psi(y)$ may be complex number, $\alpha$ is the wave number which is a real number and $c$ is the phase velocity which may be complex as well. Inserting this proposed solution leads us to the equation which is known as Rayleigh's equation.

\begin
0 &= \left(\frac + U\frac\right) \nabla^2 \psi + \frac\left(\beta - U''\right)\\ 4pt0 &= \left(\frac + U\frac\right)\left((i\alpha)^2\Psi e^ + \Psi''e^\right) + i\alpha\Psi e^(\beta - U'')\\ 4pt0 &= (i\alpha)^2\Psi e^(-i\alpha c + i\alpha U ) + \Psi''e^ (-i\alpha c+i\alpha U) + i\alpha\Psi e^(\beta - U'')\\ 4pt0 &= i\alpha e^ \alpha^2c - \alpha^2 U)\Psi + \Psi''(-c + U) + \Psi(\beta - U'')\ 4pt0 &= (U-c)(\Psi'' - \alpha^2\Psi) + (\beta - U'')\Psi)\\ 4pt\end
To get to this equation, in the last step it was used that $\alpha$ can't be zero and neither can the exponential. This means that the terms in the square brackets needs to be zero. The symbol $\Psi''$ denotes the second derivative of the amplitude of the stream function, $\Psi$ with respect to $y$ $(\Psi'' = \frac)$. This last equation that was derived, is known as Rayleigh's equation which is a linear ordinary differential equation. It is very difficult to explicitly solve this equation. It is therefore that Hsiao-Lan Kuo came up with a stability criterion for this problem without actually solving it.

Kuo Criterion

Instead of solving Rayleigh's equation, Hsiao-Lan Kuo came up with a necessary stability condition which had to be met in order for the fluid to be able to get unstable. To get to this criterion, Rayleigh's equation was rewritten and the boundary conditions of the flow field are used.

The first step is to divide Rayleigh's equation by $(U-c)$ and multiplying the equation by the complex conjugate of $\Psi\;\; (\Psi^*= \Psi_r - i\Psi_i)$.

$\begin 0 &= (\Psi'' - \alpha^2\Psi) + \left( \frac \right)\Psi\\ 0 &= \Psi^*(\Psi_r'' + i\Psi_i'' - \alpha^2\Psi_r - \alpha^2 i\Psi_i) + \Psi^*\left(\frac\right)(\Psi_r - i\Psi_i)\\ 0 &= \Psi_r\Psi_r'' + \Psi_i\Psi_i'' - \alpha^2(\Psi_r^2 - \Psi_i^2) + \left(\frac\right) (\Psi_r^2 - \Psi_i^2) + i(-\Psi_i\Psi_r'' + \Psi_r\Psi_i'')\\ 0 &= \Psi_r''\Psi_r + \Psi_i''\Psi_i + \left(-\alpha^2 + \frac(\beta - U'')\right), \Psi, ^2 + i\left(\frac(\beta - U''), \Psi, ^2 - \Psi_r''\Psi_i + \Psi_i''\Psi_r\right) \end$In the last step, $(U-c)$ is multiplied with its complex conjugate leading to the following equality is used: $\frac =\frac = \frac$. For the solution of Rayleigh's equation to exist, both the real and imaginary part of the equation above need to be equal to zero.

Boundary conditions

To get to the Kuo criterion, the imaginary part is integrated over the domain (y= ,L) . The stream function at the boundaries of the domain is zero, $\Psi(0) = \Psi(L) = 0$, as already stated in the assumptions. The zonal flow must vanish at the boundaries of the domain. This leads to a constant stream function which is set to zero for convenience.

$\int_0^L(\Psi_r\Psi_i'' - \Psi_i\Psi_r'')dy + \int_0^L\left(c_i \frac(\beta - U'')\right) =0$

The first integral can be solved:

\begin
\int_0^L (\Psi_r\Psi_i'' - \Psi_i\Psi_r'')dy &= \int_0^L \frac(\Psi_r\Psi_i' - \Psi_i\Psi_r')dy\\ pt&= (\Psi_r\Psi_i' - \Psi_i\Psi_r'), _0^L \\ pt&= 0 \\ 2pt\end

So the first integral is equal to zero. This means that the second integral should also be zero, making it possible to solve this integral numerically.

$\begin \int_0^L\left(c_i \frac(\beta - U'')\right)dy &=0\\ \end$

When $c_i$ is zero, we are dealing with a stable amplitude of the solution, this means that the solution is stable. We are looking for un unstable situation, so then $\frac(\beta - U'')$ should be zero. Since the fraction in front of $(\beta - U'')$ is non-zero and positive, this leads to the conclusion that $(\beta - U'')$ should be zero. This leads to the final formulation, the Kuo criterion:

$\begin \beta - U'' &= 0\\$0pt\beta &= U''\\0pt\frac &= \frac

\end
Here, $U$ is the mean zonal flow and $\beta$ is the derivative of the planetary vorticity $f$ with respect to $y$.

References

Fluid dynamics
{{DEFAULTSORT:Rayleigh-Kuo criterion