HOME

TheInfoList

Click Here for Items Related To - Rankine–Hugoniot Conditions

OR:

Rankine–Hugoniot Conditions on: [Wikipedia] [Google] [Amazon]

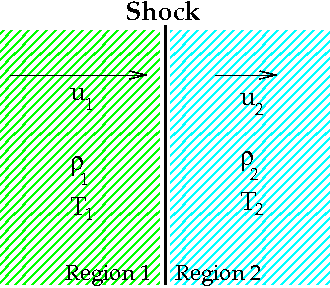Rankine Hugoniot Shock

The Rankine–Hugoniot conditions, also referred to as Rankine–Hugoniot jump conditions or Rankine–Hugoniot relations, describe the relationship between the states on both sides of a

shock wave In physics, a shock wave (also spelled shockwave), or shock, is a type of propagating disturbance that moves faster than the local speed of sound in the medium. Like an ordinary wave, a shock wave carries energy and can propagate through a me ...

or a combustion wave (

deflagration Deflagration (Lat: ''de + flagrare'', "to burn down") is subsonic combustion in which a pre-mixed flame propagates through a mixture of fuel and oxidizer. Deflagrations can only occur in pre-mixed fuels. Most fires found in daily life are diff ...

or

detonation Detonation () is a type of combustion involving a supersonic exothermic front accelerating through a medium that eventually drives a shock front propagating directly in front of it. Detonations propagate supersonically through shock waves with ...

) in a one-dimensional flow in fluids or a one-dimensional deformation in solids. They are named in recognition of the work carried out by Scottish engineer and physicist

William John Macquorn Rankine William John Macquorn Rankine (; 5 July 1820 – 24 December 1872) was a Scottish mechanical engineer who also contributed to civil engineering, physics and mathematics. He was a founding contributor, with Rudolf Clausius and William Thomson ( ...

an-70 The Antonov An-70 ( uk, link=no, Антонов Ан-70) is a four-engine medium-range Military transport aircraft, transport aircraft, and the first aircraft to take flight powered only by propfan engines. It was developed in the late 1980s b ...

> and French engineer Pierre Henri Hugoniot.ug-87> See also: Hugoniot, H. (1889
"Mémoire sur la propagation des mouvements dans les corps et spécialement dans les gaz parfaits (deuxième partie)"
emoir on the propagation of movements in bodies, especially perfect gases (second part) ''Journal de l'École Polytechnique'', vol. 58, pages 1–125.al-06> In a coordinate system that is moving with the discontinuity, the Rankine–Hugoniot conditions can be expressed as: : where ''m'' is the mass flow rate per unit area, ''ρ''₁ and ''ρ''₂ are the

mass density Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically ...

of the fluid upstream and downstream of the wave, ''u''₁ and ''u''₂ are the fluid velocity upstream and downstream of the wave, ''p''₁ and ''p''₂ are the pressures in the two regions, and ''h''₁ and ''h''₂ are the ''specific'' (with the sense of ''per unit mass'') enthalpies in the two regions. If in addition, the flow is reactive, then the species conservation equations demands that :

\omega_=\omega_=0,\quad i = 1,2,3,\dots,N, \qquad \text

to vanish both upstream and downstream of the discontinuity. Here,

\omega

is the mass production rate of the ''i''-th species of total ''N'' species involved in the reaction. Combining conservation of mass and momentum gives us :

\frac=-m^2

which defines a straight line known as the Michelson–Rayleigh line, named after

Albert A. Michelson Albert Abraham Michelson FFRS HFRSE (surname pronunciation anglicized as "Michael-son", December 19, 1852 – May 9, 1931) was a German-born American physicist of Polish/Jewish origin, known for his work on measuring the speed of light and espe ...

and

Lord Rayleigh John William Strutt, 3rd Baron Rayleigh, (; 12 November 1842 – 30 June 1919) was an English mathematician and physicist who made extensive contributions to science. He spent all of his academic career at the University of Cambridge. Amo ...

, that has a negative slope (since

m^2

is always positive) in the

p-\rho^

plane. Using the Rankine–Hugoniot equations for the conservation of mass and momentum to eliminate ''u''₁ and ''u''₂, the equation for the conservation of energy can be expressed as the Hugoniot equation: :

h_2 - h_1 = \frac\,\left(\frac+\frac\right)\,(p_2 - p_1).

The inverse of the density can also be expressed as the

specific volume In thermodynamics, the specific volume of a substance (symbol: , nu) is an intrinsic property of the substance, defined as the ratio of the substance's volume () to its mass (). It is the reciprocal of density (rho) and it is related to the ...

,

v=1/\rho

. Along with these, one has to specify the relation between the upstream and downstream equation of state :

f(p_1,\rho_1,T_1,Y_)=f(p_2,\rho_2,T_2,Y_)

where

Y_i

is the mass fraction of the species. Finally, the calorific equation of state

h=h(p,\rho,Y_i)

is assumed to be known, i.e., :

h(p_1,\rho_1,Y_)=h(p_2,\rho_2,Y_).

Simplified Rankine–Hugoniot relations

The following assumptions are made in order to simplify the Rankine–Hugoniot equations. The mixture is assumed to obey the

ideal gas law The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first st ...

, so that relation between the downstream and upstream equation of state can be written as :

\frac=\frac=\frac

where

R

is the

universal gas constant The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per ...

and the mean

molecular weight A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bioch ...

\overline W

is assumed to be constant (otherwise,

\overline W

would depend on the mass fraction of the all species). If one assumes that the

specific heat In thermodynamics, the specific heat capacity (symbol ) of a substance is the heat capacity of a sample of the substance divided by the mass of the sample, also sometimes referred to as massic heat capacity. Informally, it is the amount of he ...

at constant pressure

c_p

is also constant across the wave, the change in enthalpies (calorific equation of state) can be simply written as :

h_2-h_1 = -q + c_p(T_2-T_1)

where the first term in the above expression represents the amount of heat released per unit mass of the upstream mixture by the wave and the second term represents the sensible heating. Eliminating temperature using the equation of state and substituting the above expression for the change in enthalpies into the Hugoniot equation, one obtains a Hugoniot equation expressed only in terms of pressure and densities, :

\left(\frac\right)\left(\frac-\frac\right) - \frac\left(\frac + \frac\right)(p_2-p_1) = q,

where

\gamma

is the

specific heat ratio In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volu ...

. Hugoniot curve without heat release (

q=0

) is often called as Shock Hugoniot. Along with the Rayleigh line equation, the above equation completely determines the state of the system. These two equations can be written compactly by introducing the following non-dimensional scales, :

\tilde p = \frac,\quad \tilde v = \frac, \quad \alpha = \frac, \quad \mu = \frac.

The Rayleigh line equation and the Hugoniot equation then simplifies to :

\begin
  \frac &= -\mu \\
                       \tilde p &= \frac.
\end

Given the upstream conditions, the intersection of above two equations in the

\tilde p-\tilde v

plane determine the downstream conditions. If no heat release occurs, for example, shock waves without chemical reaction, then

\alpha=0

. The Hugoniot curves asymptote to the lines

\tilde v = (\gamma-1)/(\gamma+1)

and

\tilde p=-(\gamma-1)/(\gamma+1)

, i.e., the pressure jump across the wave can take any values between

0\leq \tilde p<\infty

, but the specific volume ratio is restricted to the interval

(\gamma-1)/(\gamma+1)\leq \tilde v \leq 2\alpha + (\gamma+1)/(\gamma-1)

(the upper bound is derived for the case

\tilde p\rightarrow 0

because pressure cannot take negative values). The

Chapman–Jouguet condition The Chapman–Jouguet condition holds approximately in detonation waves in high explosives. It states that the detonation propagates at a velocity at which the reacting gases just reach sonic velocity (in the frame of the leading shock wave) as th ...

is where Rayleigh line is tangent to the Hugoniot curve. If

\gamma=1.4

(diatomic gas without the vibrational mode excitation), the interval is

1/6\leq \tilde v\leq 2\alpha + 6

, in other words, the shock wave can increase the density at most by a factor of 6. For monatomic gas,

\gamma=5/3

, therefore the density ratio is limited by the interval

1/4\leq \tilde v\leq 2\alpha + 4

. For diatomic gases with vibrational mode excited, we have

\gamma=9/7

leading to the interval

1/8\leq \tilde v\leq 2\alpha + 8

. In reality, the specific heat ratio is not constant in the shock wave due to molecular dissociation and ionization, but even in these cases, density ratio in general do not exceed the factor

11-13

.

Derivation from Euler equations

Consider gas in a one-dimensional container (e.g., a long thin tube). Assume that the fluid is

inviscid The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the inte ...

(i.e., it shows no viscosity effects as for example friction with the tube walls). Furthermore, assume that there is no heat transfer by conduction or radiation and that gravitational acceleration can be neglected. Such a system can be described by the following system of

conservation law In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of energy, conservation of linear momentum, ...

s, known as the 1D

Euler equations 200px, Leonhard Euler (1707–1783) In mathematics and physics, many topics are named in honor of Swiss mathematician Leonhard Euler (1707–1783), who made many important discoveries and innovations. Many of these items named after Euler includ ...

, that in conservation form is: where *

\rho,

fluid

mass density Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically ...

, *

u,

fluid

velocity Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity i ...

, *

e,

specific

internal energy The internal energy of a thermodynamic system is the total energy contained within it. It is the energy necessary to create or prepare the system in its given internal state, and includes the contributions of potential energy and internal kinet ...

of the fluid, *

p,

fluid

pressure Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country a ...

, and *

E^t = \rho e + \rho\tfracu^2,

is the total energy density of the fluid, /m³ while ''e'' is its specific internal energy Assume further that the gas is calorically ideal and that therefore a polytropic equation-of-state of the simple form is valid, where

\gamma

is the constant ratio of specific heats

c_p/c_v

. This quantity also appears as the ''polytropic exponent'' of the polytropic process described by For an extensive list of compressible flow equations, etc., refer to

NACA The National Advisory Committee for Aeronautics (NACA) was a United States federal agency founded on March 3, 1915, to undertake, promote, and institutionalize aeronautical research. On October 1, 1958, the agency was dissolved and its assets ...

Report 1135 (1953).me-53> Note: For a calorically ideal gas

\gamma

is a constant and for a thermally ideal gas

\gamma

is a function of temperature. In the latter case, the dependence of pressure on mass density and internal energy might differ from that given by equation ().

The jump condition

Before proceeding further it is necessary to introduce the concept of a ''jump condition'' – a condition that holds at a discontinuity or abrupt change. Consider a 1D situation where there is a jump in the scalar conserved physical quantity

w

, which is governed by integral conservation law for any

x_1

,

x_2

,

x_1, and, therefore, by partial differential equation 


for smooth solutions.

Let the solution exhibit a jump (or shock) at x=x_(t), where x_ < x_(t) and x_(t) < x_, then




The subscripts 1 and 2 indicate conditions ''just  upstream'' and ''just downstream'' of the jump respectively, i.e. w_1 = \lim_ w\left(x_s - \epsilon\right) and 

Note, to arrive at equation () we have used the fact that dx_1/dt = 0 and dx_2/dt = 0 .

Now, let x_1 \to x_s(t) - \epsilon and x_2 \to x_s(t) + \epsilon, when we have \int_^ w_t \, dx \to 0 and \int_^ w_t \, dx \to 0, and in the limit



where we have defined u_s = dx_s(t)/dt (the system ''characteristic'' or ''shock speed''), which by simple division is given by



Equation () represents the jump condition for conservation law ().  A shock situation arises in a system where its ''characteristics'' intersect, and under these conditions a requirement for a unique single-valued solution is that the solution should satisfy the ''admissibility condition'' or ''entropy condition''. For physically real applications this means that the solution should satisfy the ''Lax entropy condition''



where f'\left(w_1\right) and f'\left(w_2\right) represent ''characteristic speeds'' at upstream and downstream conditions respectively.

Shock condition

In the case of the hyperbolic conservation law (), we have seen that the shock speed can be obtained by simple division. However, for the 1D Euler equations (), () and (), we have the vector state variable

\begin\rho & \rho u & E\end^\mathsf

and the jump conditions become Equations (), () and () are known as the ''Rankine–Hugoniot conditions'' for the Euler equations and are derived by enforcing the conservation laws in integral form over a control volume that includes the shock. For this situation

u_s

cannot be obtained by simple division. However, it can be shown by transforming the problem to a moving co-ordinate system (setting

u_s' := u_s - u_1

,

u'_1 := 0

,

u'_2 := u_2 - u_1

to remove

u_1

) and some algebraic manipulation (involving the elimination of

u'_2

from the transformed equation () using the transformed equation ()), that the shock speed is given by where

c_=\sqrt

is the speed of sound in the fluid at upstream conditions.hi-99>

Shock Hugoniot and Rayleigh line in solids

HugoniotRaleigh

For shocks in solids, a closed form expression such as equation () cannot be derived from first principles. Instead, experimental observations indicate that a linear relation Though a linear relation is widely assumed to hold, experimental data suggest that almost 80% of tested materials do not satisfy this widely accepted linear behavior. See Kerley, G. I, 2006, "The Linear US-uP Relation in Shock-Wave Physics", ; for details. can be used instead (called the shock Hugoniot in the ''u''_s-''u''_p plane) that has the form where ''c''₀ is the bulk speed of sound in the material (in uniaxial compression), ''s'' is a parameter (the slope of the shock Hugoniot) obtained from fits to experimental data, and is the particle velocity inside the compressed region behind the shock front. The above relation, when combined with the Hugoniot equations for the conservation of mass and momentum, can be used to determine the shock Hugoniot in the ''p''-''v'' plane, where ''v'' is the specific volume (per unit mass):Poirier, J-P. (2008) "Introduction to the Physics of the Earth's Interior", Cambridge University Press. Alternative equations of state, such as the

Mie–Grüneisen equation of state The Mie–Grüneisen equation of state is an equation of state that relates the pressure and volume of a solid at a given temperature.Roberts, J. K., & Miller, A. R. (1954). Heat and thermodynamics (Vol. 4). Interscience Publishers.Burshtein, A. I. ...

may also be used instead of the above equation. The shock Hugoniot describes the locus of all possible

thermodynamic state In thermodynamics, a thermodynamic state of a system is its condition at a specific time; that is, fully identified by values of a suitable set of parameters known as state variables, state parameters or thermodynamic variables. Once such a set ...

s a material can exist in behind a shock, projected onto a two dimensional state-state plane. It is therefore a set of equilibrium states and does not specifically represent the path through which a material undergoes transformation. Weak shocks are

isentropic In thermodynamics, an isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized proce ...

and that the isentrope represents the path through which the material is loaded from the initial to final states by a compression wave with converging characteristics. In the case of weak shocks, the Hugoniot will therefore fall directly on the isentrope and can be used directly as the equivalent path. In the case of a strong shock we can no longer make that simplification directly. However, for engineering calculations, it is deemed that the isentrope is close enough to the Hugoniot that the same assumption can be made. If the Hugoniot is approximately the loading path between states for an "equivalent" compression wave, then the jump conditions for the shock loading path can be determined by drawing a straight line between the initial and final states. This line is called the Rayleigh line and has the following equation:

Hugoniot elastic limit

Most solid materials undergo

plastic Plastics are a wide range of synthetic or semi-synthetic materials that use polymers as a main ingredient. Their plasticity makes it possible for plastics to be moulded, extruded or pressed into solid objects of various shapes. This adaptab ...

deformations when subjected to strong shocks. The point on the shock Hugoniot at which a material transitions from a purely

elastic Elastic is a word often used to describe or identify certain types of elastomer, elastic used in garments or stretchable fabrics. Elastic may also refer to: Alternative name * Rubber band, ring-shaped band of rubber used to hold objects togethe ...

state to an elastic-plastic state is called the Hugoniot elastic limit (HEL) and the pressure at which this transition takes place is denoted ''p''_HEL. Values of ''p''_HEL can range from 0.2 GPa to 20 GPa. Above the HEL, the material loses much of its shear strength and starts behaving like a fluid.

See also

*

Euler equations (fluid dynamics) In fluid dynamics, the Euler equations are a set of quasilinear partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with ze ...

*

Shock polar The term ''shock polar'' is generally used with the graphical representation of the Rankine–Hugoniot equations in either the hodograph plane or the pressure ratio-flow deflection angle plane. The polar itself is the locus of all possible states a ...

*

Mie–Grüneisen equation of state The Mie–Grüneisen equation of state is an equation of state that relates the pressure and volume of a solid at a given temperature.Roberts, J. K., & Miller, A. R. (1954). Heat and thermodynamics (Vol. 4). Interscience Publishers.Burshtein, A. I. ...

* Engineering Acoustics Wikibook *

Atmospheric focusing Atmospheric focusing is a type of wave interaction causing shock wave, shock waves to affect areas at a greater distance than otherwise expected. Variations in the atmosphere create distortions in the wavefront by Refraction, refracting a segment, ...

References

{{DEFAULTSORT:Rankine-Hugoniot Conditions Equations of fluid dynamics Scottish inventions Conservation equations Continuum mechanics Combustion Fluid dynamics