Quantum Computational Chemistry

Quantum computational chemistry is an emerging field that exploits quantum computing to simulate chemical systems. Despite quantum mechanics' foundational role in understanding chemical behaviors, traditional computational approaches face significant challenges, largely due to the complexity and computational intensity of quantum mechanical equations. This complexity arises from the exponential growth of a quantum system's wave function with each added particle, making exact simulations on classical computers inefficient.

Efficient quantum algorithms for chemistry problems are expected to have run-times and resource requirements that scale polynomially with system size and desired accuracy. Experimental efforts have validated proof-of-principle chemistry calculations, though currently limited to small systems.

Brief History of Quantum Computational Chemistry

* 1929: Dirac noted the inherent complexity of quantum mechanical equations, underscoring the difficulties in solving these equations using classical computation.
* 1982: Feynman proposed using quantum hardware for simulations, addressing the inefficiency of classical computers in simulating quantum systems.

Common Methods in Quantum Computational Chemistry

While there are several common methods in quantum chemistry, the section below lists only a few examples.

Qubitization

Qubitization is a mathematical and algorithmic concept in quantum computing for the simulation of quantum systems via Hamiltonian dynamics. The core idea of qubitization is to encode the problem of Hamiltonian simulation in a way that is more efficiently processable by quantum algorithms.

Qubitization involves a transformation of the Hamiltonian operator, a central object in quantum mechanics representing the total energy of a system. In classical computational terms, a Hamiltonian can be thought of as a matrix describing the energy interactions within a quantum system. The goal of qubitization is to embed this Hamiltonian into a larger, unitary operator, which is a type of operator in quantum mechanics that preserves the norm of vectors upon which it acts.

Mathematically, the process of qubitization constructs a unitary operator $U$ such that a specific projection of $U$ is proportional to the Hamiltonian $H$ of interest. This relationship can often be represented as $H = \langle G , U , G \rangle$, where  $, G \rangle$ is a specific quantum state and $\langle G ,$ is its conjugate transpose. The efficiency of this method comes from the fact that the unitary operator $U$ can be implemented on a quantum computer with fewer resources (like qubits and quantum gates) than would be required for directly simulating $H.$

A key feature of qubitization is in simulating Hamiltonian dynamics with high precision while reducing the quantum resource overhead. This efficiency is especially beneficial in quantum algorithms where the simulation of complex quantum systems is necessary, such as in quantum chemistry and materials science simulations. Qubitization also develops quantum algorithms for solving certain types of problems more efficiently than classical algorithms. For instance, it has implications for the Quantum Phase Estimation algorithm, which is fundamental in various quantum computing applications, including factoring and solving linear systems of equations.

Applications of qubitization in chemistry

= Gaussian orbital basis sets

=

In Gaussian orbital basis sets, phase estimation algorithms have been optimized empirically from $\mathcal(M^)$ to $\mathcal(M^)$ where $M$ is the number of basis sets. Advanced Hamiltonian simulation algorithms have further reduced the scaling, with the introduction of techniques like Taylor series methods and qubitization, providing more efficient algorithms with reduced computational requirements.

= Plane wave basis sets

=

Plane wave basis sets, suitable for periodic systems, have also seen advancements in algorithm efficiency, with improvements in product formula-based approaches and Taylor series methods.

Quantum phase estimation in chemistry

Overview

Phase estimation, as proposed by Kitaev in 1996, identifies the lowest energy eigenstate ( $, E_0 \rangle$ ) and excited states ( $, E_i \rangle$ ) of a physical Hamiltonian, as detailed by Abrams and Lloyd in 1999. In quantum computational chemistry, this technique is employed to encode fermionic Hamiltonians into a qubit framework.

Brief methodology

Initialization

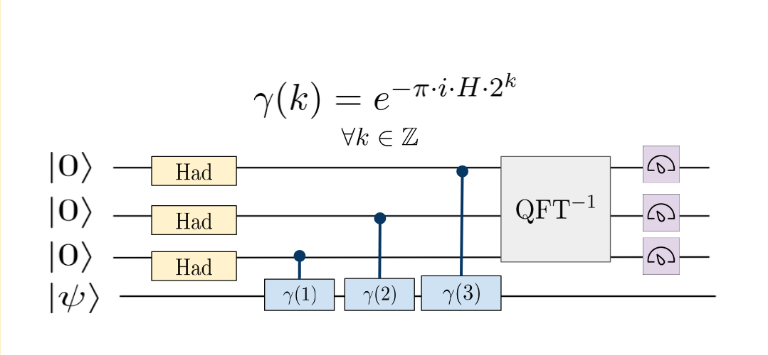
The qubit register is initialized in a state, which has a nonzero overlap with the Full Configuration Interaction (FCI) target eigenstate of the system. This state $, \psi \rangle$ is expressed as a sum over the energy eigenstates of the Hamiltonian, $, \psi \rangle = \sum_ c_i , E_i \rangle$ , where $c_i$represents complex coefficients.

Application of Hadamard gates

Each ancilla qubit undergoes a Hadamard gate application, placing the ancilla register in a superposed state. Subsequently, controlled gates, as shown above, modify this state.

Inverse quantum fourier transform

This transform is applied to the ancilla qubits, revealing the phase information that encodes the energy eigenvalues.

Measurement

The ancilla qubits are measured in the Z basis, collapsing the main register into the corresponding energy eigenstate $, E_i \rangle$ based on the probability $, c_i, ^2$.

Requirements

The algorithm requires $\omega$ ancilla qubits, with their number determined by the desired precision and success probability of the energy estimate. Obtaining a binary energy estimate precise to n bits with a success probability $p$ necessitates.$\omega = n + \lceil \log_2 \left(2 + \frac\right) \rceil$ ancilla qubits. This phase estimation has been validated experimentally across various quantum architectures.

Applications of QPEs in chemistry

Time evolution and error analysis

The total coherent time evolution $T$ required for the algorithm is approximately $T = 2^\pi$. The total evolution time is related to the binary precision $\varepsilon_ = \frac$, with an expected repeat of the procedure for accurate ground state estimation. Errors in the algorithm include errors in energy eigenvalue estimation ($\varepsilon_$), unitary evolutions ($\varepsilon_$), and circuit synthesis errors ($\varepsilon_$), which can be quantified using techniques like the Solovay-Kitaev theorem.

The phase estimation algorithm can be enhanced or altered in several ways, such as using a single ancilla qubit  for sequential measurements, increasing efficiency, parallelization, or enhancing noise resilience in analytical chemistry. The algorithm can also be scaled using classically obtained knowledge about energy gaps between states.

Limitations

Effective state preparation is needed, as a randomly chosen state would exponentially decrease the probability of collapsing to the desired ground state. Various methods for state preparation have been proposed, including classical approaches and quantum techniques like adiabatic state preparation.

Variational quantum eigensolver (VQE)

Overview

The variational quantum eigensolver is an algorithm in quantum computing, crucial for near-term quantum hardware. Initially proposed by Peruzzo et al. in 2014 and further developed by McClean et al. in 2016, VQE finds the lowest eigenvalue of Hamiltonians, particularly those in chemical systems. It employs the variational method (quantum mechanics), which guarantees that the expectation value of the Hamiltonian for any parameterized trial wave function is at least the lowest energy eigenvalue of that Hamiltonian. VQE is a hybrid algorithm that utilizes both quantum and classical computers. The quantum computer prepares and measures the quantum state, while the classical computer processes these measurements and updates the system. This synergy allows VQE to overcome some limitations of purely quantum methods.

Applications of VQEs in chemistry

= 1-RDM and 2-RDM calculations

=

The reduced density matrices (1-RDM and 2-RDM) can be used to extrapolate the electronic structure of a system.

= Ground state energy extrapolation

=

In the Hamiltonian variational ansatz, the initial state $, \psi_0\rangle$  is prepared to represent the ground state of the molecular Hamiltonian without electron correlations. The evolution of this state under the Hamiltonian, split into commuting segments $H_j$ , is given by the equation below.

$, \psi(\theta)\rangle = \prod_d \prod_j e^ , \psi_0\rangle$

where $\theta_$  are variational parameters optimized to minimize the energy, providing insights into the electronic structure of the molecule.

= Measurement scaling

=

McClean et al. (2016) and Romero et al. (2019) proposed a formula to estimate the number of measurements ( $N_m$ ) required for energy precision. The formula is given by $N_m = \left(\sum_i , h_i, \right)^2/\epsilon^2$ , where $h_i$ are coefficients of each Pauli string in the Hamiltonian. This leads to a scaling of $\mathcal(M^6/\epsilon^2)$ in a Gaussian orbital basis and $\mathcal(M^4/\epsilon^2)$ in a plane wave dual basis. Note that $M$ is the number of basis functions in the chosen basis set.

= Fermionic level grouping

=

A method by Bonet-Monroig, Babbush, and O'Brien (2019) focuses on grouping terms at a fermionic level rather than a qubit level, leading to a measurement requirement of only $\mathcal(M^2)$ circuits with an additional gate depth of $\mathcal(M)$.

= Limitations of VQE

=

While VQE's application in solving the electronic Schrödinger equation for small molecules has shown success, its scalability is hindered by two main challenges: the complexity of the quantum circuits required and the intricacies involved in the classical optimization process. These challenges are significantly influenced by the choice of the variational ansatz, which is used to construct the trial wave function. Modern quantum computers face limitations in running deep quantum circuits, especially when using the existing ansatzes for problems that exceed several qubits.

Jordan-Wigner encoding

Jordan-Wigner encoding is a method in quantum computing used for simulating fermionic systems like molecular orbitals and electron interactions in quantum chemistry.

Overview

In quantum chemistry, electrons are modeled as fermions with antisymmetric wave functions. The Jordan-Wigner encoding maps these fermionic orbitals to qubits, preserving their antisymmetric nature. Mathematically, this is achieved by associating each fermionic creation $( a^\dagger_i )$ and annihilation $( a_i )$ operator with corresponding qubit operators through the Jordan-Wigner transformation:

$a^\dagger_i \rightarrow \frac \left( \prod_^ Z_k \right) (X_i - iY_i)$

Where $X_i$ , $Y_i$ , and $Z_i$ are Pauli matrices acting on the $i^$ qubit.

Applications of Jordan-Wigner encoding in chemistry

= Electron hopping

=

Electron hopping between orbitals, central to chemical bonding and reactions, is represented by terms like $a^ a_j + a^ a_i$. Under Jordan-Wigner encoding, these transform as follows:$a^\dagger_i a_j + a^\dagger_j a_i \rightarrow \frac (X_i X_j + Y_i Y_j) Z_ \cdots Z_$This transformation captures the quantum mechanical behavior of electron movement and interaction within molecules.

= Computational complexity in molecular systems

=

The complexity of simulating a molecular system using Jordan-Wigner encoding is influenced by the structure of the molecule and the nature of electron interactions. For a molecular system with $K$ orbitals, the number of required qubits scales linearly with $K$ , but the complexity of gate operations depends on the specific interactions being modeled.

Limitations of Jordan–Wigner encoding

The Jordan-Wigner transformation encodes fermionic operators into qubit operators, but it introduces non-local string operators that can make simulations inefficient. The FSWAP gate is used to mitigate this inefficiency by rearranging the ordering of fermions (or their qubit representations), thus simplifying the implementation of fermionic operations.

Fermionic SWAP (FSWAP) network

FSWAP networks rearrange qubits to efficiently simulate electron dynamics in molecules. These networks are essential for reducing the gate complexity in simulations, especially for non-neighboring electron interactions.

When two fermionic modes (represented as qubits after the Jordan-Wigner transformation) are swapped, the FSWAP gate not only exchanges their states but also correctly updates the phase of the wavefunction to maintain fermionic antisymmetry. This is in contrast to the standard SWAP gate, which does not account for the phase change required in the antisymmetric wavefunctions of fermions.

The use of FSWAP gates can significantly reduce the complexity of quantum circuits for simulating fermionic systems. By intelligently rearranging the fermions, the number of gates required to simulate certain fermionic operations can be reduced, leading to more efficient simulations. This is particularly useful in simulations where fermions need to be moved across large distances within the system, as it can avoid the need for long chains of operations that would otherwise be required.

References

Quantum chemistry

Further reading

*
*

{{subject bar, auto=y, d=y, portal=chemistry