Pseudo-convex Function on:
[Wikipedia]
[Google]
[Amazon]
In
 To see that is not pseudoconvex, consider its derivative at : . Then, if was pseudoconvex, we should have:
In particular it should be true for . But it is not, as: .
To see that is not pseudoconvex, consider its derivative at : . Then, if was pseudoconvex, we should have:
In particular it should be true for . But it is not, as: .
 Finally, note that a pseudoconvex function may not have any critical point. Take for example the pseudoconvex function: , whose derivative is always positive: .
Finally, note that a pseudoconvex function may not have any critical point. Take for example the pseudoconvex function: , whose derivative is always positive: .
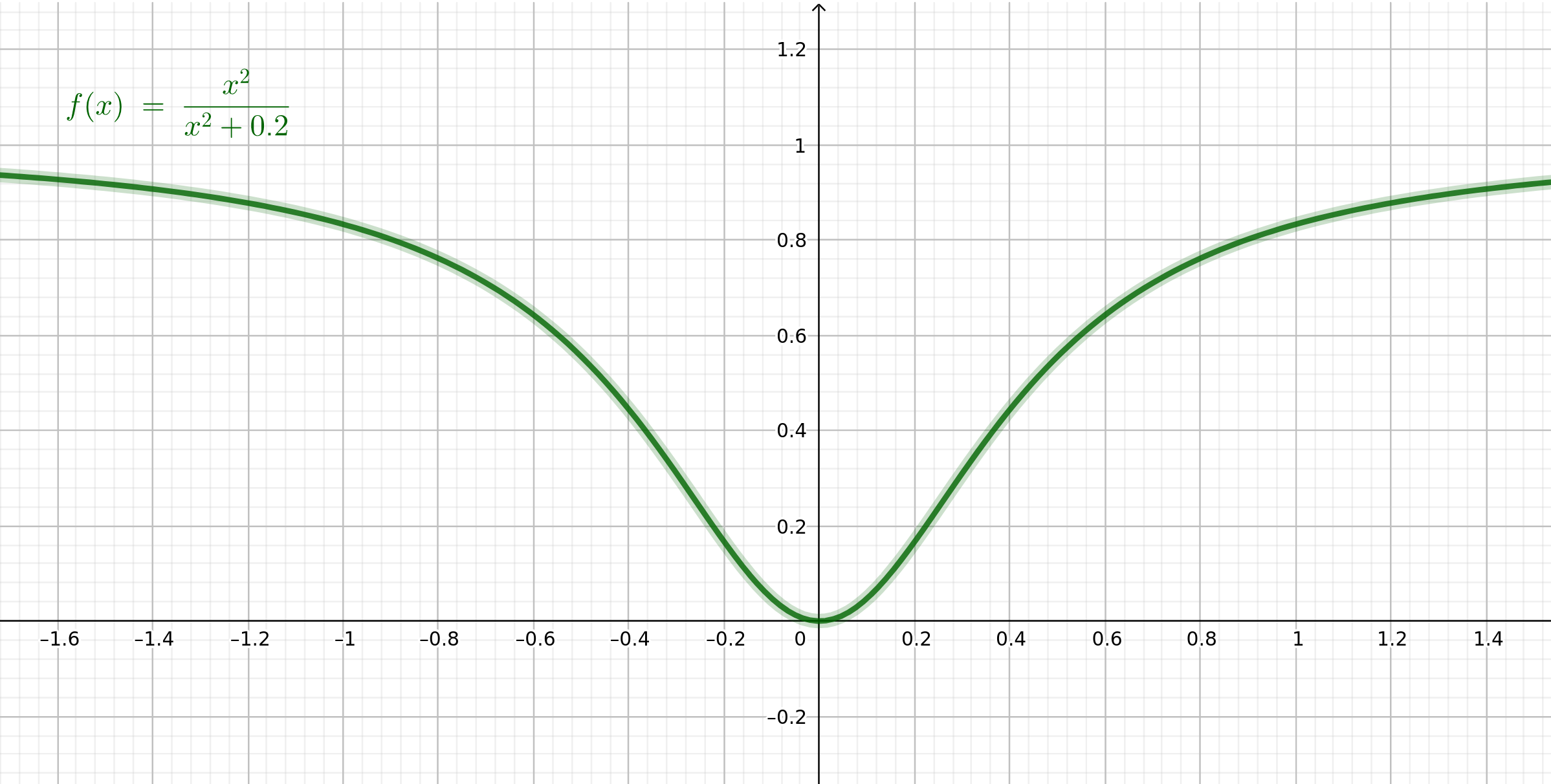 The previous example may be modified to obtain a function that is not convex, nor pseudoconvex, but is quasiconvex:
The figure shows this function for the case where . As can be seen, this function is not convex because of the concavity, and it is not pseudoconvex because it is not differentiable at .
The previous example may be modified to obtain a function that is not convex, nor pseudoconvex, but is quasiconvex:
The figure shows this function for the case where . As can be seen, this function is not convex because of the concavity, and it is not pseudoconvex because it is not differentiable at .
convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex optimization, convex minimization, a subdomain of optimization (mathematics), optimization theor ...
and the calculus of variations
The calculus of variations (or variational calculus) is a field of mathematical analysis that uses variations, which are small changes in Function (mathematics), functions
and functional (mathematics), functionals, to find maxima and minima of f ...
, both branches of mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a pseudoconvex function is a function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-orie ...
that behaves like a convex function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is conve ...
with respect to finding its local minima
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative' ...
, but need not actually be convex. Informally, a differentiable function is pseudoconvex if it is increasing in any direction where it has a positive directional derivative
In multivariable calculus, the directional derivative measures the rate at which a function changes in a particular direction at a given point.
The directional derivative of a multivariable differentiable (scalar) function along a given vect ...
. The property must hold in all of the function domain, and not only for nearby points.
Formal definition
Consider adifferentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in ...
function , defined on a (nonempty) convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
open set
In mathematics, an open set is a generalization of an Interval (mathematics)#Definitions_and_terminology, open interval in the real line.
In a metric space (a Set (mathematics), set with a metric (mathematics), distance defined between every two ...
of the finite-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. This function is said to be pseudoconvex if the following property holds:
Equivalently:
Here is the gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The g ...
of , defined by:
Note that the definition may also be stated in terms of the directional derivative
In multivariable calculus, the directional derivative measures the rate at which a function changes in a particular direction at a given point.
The directional derivative of a multivariable differentiable (scalar) function along a given vect ...
of , in the direction given by the vector . This is because, as is differentiable, this directional derivative is given by:
Properties
Relation to other types of "convexity"
Every convex function is pseudoconvex, but the converse is not true. For example, the function is pseudoconvex but not convex. Similarly, any pseudoconvex function isquasiconvex
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form (-\infty,a) is a convex set. For a function of a singl ...
; but the converse is not true, since the function is quasiconvex but not pseudoconvex. This can be summarized schematically as:
Sufficient optimality condition
For any differentiable function, we have the Fermat's theorem necessary condition of optimality, which states that: if has a local minimum at in anopen
Open or OPEN may refer to:
Music
* Open (band), Australian pop/rock band
* The Open (band), English indie rock band
* ''Open'' (Blues Image album), 1969
* ''Open'' (Gerd Dudek, Buschi Niebergall, and Edward Vesala album), 1979
* ''Open'' (Go ...
domain, then must be a stationary point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of a function, graph of the function where the function's derivative is zero. Informally, it is a point where the ...
of (that is: ).
Pseudoconvexity is of great interest in the area of optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
, because the converse is also true for any pseudoconvex function. That is: if is a stationary point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of a function, graph of the function where the function's derivative is zero. Informally, it is a point where the ...
of a pseudoconvex function , then has a global minimum at . Note also that the result guarantees a global minimum (not only local).
This last result is also true for a convex function, but it is not true for a quasiconvex function. Consider for example the quasiconvex function:
This function is not pseudoconvex, but it is quasiconvex. Also, the point is a critical point of , as . However, does not have a global minimum at (not even a local minimum).
Examples
An example of a function that is pseudoconvex, but not convex, is: The figure shows this function for the case where . This example may be generalized to two variables as: The previous example may be modified to obtain a function that is not convex, nor pseudoconvex, but is quasiconvex:
The figure shows this function for the case where . As can be seen, this function is not convex because of the concavity, and it is not pseudoconvex because it is not differentiable at .
The previous example may be modified to obtain a function that is not convex, nor pseudoconvex, but is quasiconvex:
The figure shows this function for the case where . As can be seen, this function is not convex because of the concavity, and it is not pseudoconvex because it is not differentiable at .
Generalization to nondifferentiable functions
The notion of pseudoconvexity can be generalized to nondifferentiable functions as follows. Given any function , we can define the upperDini derivative
In mathematics and, specifically, real analysis, the Dini derivatives (or Dini derivates) are a class of generalizations of the derivative. They were introduced by Ulisse Dini, who studied continuous but nondifferentiable functions.
The upper Dini ...
of by:
where ''u'' is any unit vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ...
. The function is said to be pseudoconvex if it is increasing in any direction where the upper Dini derivative is positive. More precisely, this is characterized in terms of the subdifferential
In mathematics, the subderivative (or subgradient) generalizes the derivative to convex functions which are not necessarily Differentiable function, differentiable. The set of subderivatives at a point is called the subdifferential at that point. ...
as follows:
where