Point-spread Function on:
[Wikipedia]
[Google]
[Amazon]
The point spread function (PSF) describes the response of a focused optical imaging system to a
 When the object is divided into discrete point objects of varying intensity, the image is computed as a sum of the PSF of each point. As the PSF is typically determined entirely by the imaging system (that is, microscope or telescope), the entire image can be described by knowing the optical properties of the system. This imaging process is usually formulated by a
When the object is divided into discrete point objects of varying intensity, the image is computed as a sum of the PSF of each point. As the PSF is typically determined entirely by the imaging system (that is, microscope or telescope), the entire image can be described by knowing the optical properties of the system. This imaging process is usually formulated by a
 In
In
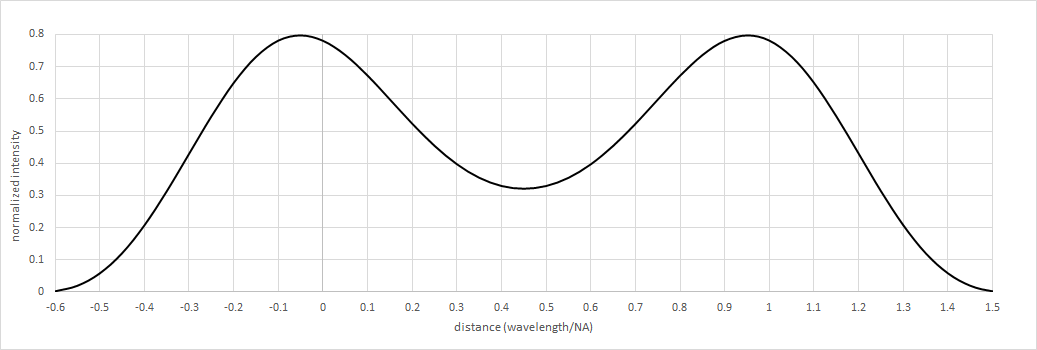 The PSF is also a fundamental limit to the conventional focused imaging of a hole,The Natural Resolution
The PSF is also a fundamental limit to the conventional focused imaging of a hole,The Natural Resolution
/ref> with the minimum printed size being in the range of 0.6-0.7 wavelength/NA, with NA being the
point source
A point source is a single identifiable ''localized'' source of something. A point source has a negligible extent, distinguishing it from other source geometries. Sources are called point sources because, in mathematical modeling, these sources ...
or point object. A more general term for the PSF is the system's impulse response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reac ...
; the PSF is the impulse response or impulse response function (IRF) of a focused optical imaging system.
The PSF in many contexts can be thought of as the shapeless blob in an image that should represent a single point object.
We can consider this as a spatial impulse response function.
In functional terms, it is the spatial domain version (i.e., the inverse Fourier transform) of the optical transfer function (OTF) of an imaging system. It is a useful concept in Fourier optics, astronomical imaging, medical imaging
Medical imaging is the technique and process of imaging the interior of a body for clinical analysis and medical intervention, as well as visual representation of the function of some organs or tissues (physiology). Medical imaging seeks to revea ...
, electron microscopy
An electron microscope is a microscope that uses a beam of electrons as a source of illumination. It uses electron optics that are analogous to the glass lenses of an optical light microscope to control the electron beam, for instance focusing i ...
and other imaging techniques such as 3D microscopy
Microscopy is the technical field of using microscopes to view subjects too small to be seen with the naked eye (objects that are not within the resolution range of the normal eye). There are three well-known branches of microscopy: optical mic ...
(like in confocal laser scanning microscopy
Confocal microscopy, most frequently confocal laser scanning microscopy (CLSM) or laser scanning confocal microscopy (LSCM), is an optical imaging technique for increasing optical resolution and contrast of a micrograph by means of using a s ...
) and fluorescence microscopy.
The degree of spreading (blurring) in the image of a point object for an imaging system is a measure of the quality of the imaging system. In non-coherent imaging systems, such as fluorescent
Fluorescence is one of two kinds of photoluminescence, the emission of light by a substance that has absorbed light or other electromagnetic radiation. When exposed to ultraviolet radiation, many substances will glow (fluoresce) with color ...
microscopes
A microscope () is a laboratory instrument used to examine objects that are too small to be seen by the naked eye. Microscopy is the science of investigating small objects and structures using a microscope. Microscopic means being invisibl ...
, telescopes
A telescope is a device used to observe distant objects by their emission, Absorption (electromagnetic radiation), absorption, or Reflection (physics), reflection of electromagnetic radiation. Originally, it was an optical instrument using len ...
or optical microscopes, the image formation process is linear in the image intensity and described by a linear system
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator.
Linear systems typically exhibit features and properties that are much simpler than the nonlinear case.
As a mathematical abstractio ...
theory. This means that when two objects A and B are imaged simultaneously by a non-coherent imaging system, the resulting image is equal to the sum of the independently imaged objects. In other words: the imaging of A is unaffected by the imaging of B and ''vice versa'', owing to the non-interacting property of photons. In space-invariant systems, i.e. those in which the PSF is the same everywhere in the imaging space, the image of a complex object is then the convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...
of that object and the PSF. The PSF can be derived from diffraction integrals.
Introduction
By virtue of the linearity property of optical ''non-coherent'' imaging systems, i.e., : ''Image''(''Object''1 + ''Object''2) = ''Image''(''Object''1) + ''Image''(''Object''2) the image of an object in a microscope or telescope as a non-coherent imaging system can be computed by expressing the object-plane field as a weighted sum of 2D impulse functions, and then expressing the image plane field as a weighted sum of the ''images'' of these impulse functions. This is known as the ''superposition principle'', valid for linear systems. The images of the individual object-plane impulse functions are called point spread functions (PSF), reflecting the fact that a mathematical ''point'' of light in the object plane is ''spread'' out to form a finite area in the image plane. (In some branches of mathematics and physics, these might be referred to as Green's functions orimpulse response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reac ...
functions. PSFs are considered impulse response functions for imaging systems.
 When the object is divided into discrete point objects of varying intensity, the image is computed as a sum of the PSF of each point. As the PSF is typically determined entirely by the imaging system (that is, microscope or telescope), the entire image can be described by knowing the optical properties of the system. This imaging process is usually formulated by a
When the object is divided into discrete point objects of varying intensity, the image is computed as a sum of the PSF of each point. As the PSF is typically determined entirely by the imaging system (that is, microscope or telescope), the entire image can be described by knowing the optical properties of the system. This imaging process is usually formulated by a convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...
equation. In microscope image processing and astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
, knowing the PSF of the measuring device is very important for restoring the (original) object with deconvolution. For the case of laser beams, the PSF can be mathematically modeled using the concepts of Gaussian beam
In optics, a Gaussian beam is an idealized beam of electromagnetic radiation whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or ...
s. For instance, deconvolution of the mathematically modeled PSF and the image, improves visibility of features and removes imaging noise.
Theory
The point spread function may be independent of position in the object plane, in which case it is called ''shift invariant''. In addition, if there is no distortion in the system, the image plane coordinates are linearly related to the object plane coordinates via themagnification
Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a size ratio called optical magnification. When this number is less than one, it refers to a reduction in size, so ...
''M'' as:
:.
If the imaging system produces an inverted image, we may simply regard the image plane coordinate axes as being reversed from the object plane axes. With these two assumptions, i.e., that the PSF is shift-invariant ''and'' that there is no distortion, calculating the image plane convolution integral is a straightforward process.
Mathematically, we may represent the object plane field as:
:
i.e., as a sum over weighted impulse functions, although this is also really just stating the shifting property of 2D delta functions (discussed further below). Rewriting the object transmittance function in the form above allows us to calculate the image plane field as the superposition of the images of each of the individual impulse functions, i.e., as a superposition over weighted point spread functions in the image plane using the ''same'' weighting function as in the object plane, i.e., . Mathematically, the image is expressed as:
:
in which is the image of the impulse function .
The 2D impulse function may be regarded as the limit (as side dimension ''w'' tends to zero) of the "square post" function, shown in the figure below.
We imagine the object plane as being decomposed into square areas such as this, with each having its own associated square post function. If the height, ''h'', of the post is maintained at 1/w2, then as the side dimension ''w'' tends to zero, the height, ''h'', tends to infinity in such a way that the volume (integral) remains constant at 1. This gives the 2D impulse the sifting property (which is implied in the equation above), which says that when the 2D impulse function, δ(''x'' − ''u'',''y'' − ''v''), is integrated against any other continuous function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More preci ...
, , it "sifts out" the value of ''f'' at the location of the impulse, i.e., at the point .
The concept of a perfect point source object is central to the idea of PSF. However, there is no such thing in nature as a perfect mathematical point source radiator; the concept is completely non-physical and is rather a mathematical construct used to model and understand optical imaging systems. The utility of the point source concept comes from the fact that a point source in the 2D object plane can only radiate a perfect uniform-amplitude, spherical wave — a wave having perfectly spherical, outward travelling phase fronts with uniform intensity everywhere on the spheres (see Huygens–Fresnel principle). Such a source of uniform spherical waves is shown in the figure below. We also note that a perfect point source radiator will not only radiate a uniform spectrum of propagating plane waves, but a uniform spectrum of exponentially decaying ( evanescent) waves as well, and it is these which are responsible for resolution finer than one wavelength (see Fourier optics). This follows from the following Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
expression for a 2D impulse function,
:
The quadratic lens
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements'') ...
intercepts a ''portion'' of this spherical wave, and refocuses it onto a blurred point in the image plane. For a single lens
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements'') ...
, an on-axis point source in the object plane produces an Airy disc PSF in the image plane. It can be shown (see Fourier optics, Huygens–Fresnel principle, Fraunhofer diffraction) that the field radiated by a planar object (or, by reciprocity, the field converging onto a planar image) is related to its corresponding source (or image) plane distribution via a Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
(FT) relation. In addition, a uniform function over a circular area (in one FT domain) corresponds to in the other FT domain, where is the first-order Bessel function
Bessel functions, named after Friedrich Bessel who was the first to systematically study them in 1824, are canonical solutions of Bessel's differential equation
x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0
for an arbitrary complex ...
of the first kind. That is, a uniformly-illuminated circular aperture that passes a converging uniform spherical wave yields an Airy disk
In optics, the Airy disk (or Airy disc) and Airy pattern are descriptions of the best-focus (optics), focused Point source#Light, spot of light that a perfect lens (optics), lens with a circular aperture can make, limited by the diffraction of ...
image at the focal plane. A graph of a sample Airy disk
In optics, the Airy disk (or Airy disc) and Airy pattern are descriptions of the best-focus (optics), focused Point source#Light, spot of light that a perfect lens (optics), lens with a circular aperture can make, limited by the diffraction of ...
is shown in the adjoining figure.
Therefore, the converging (''partial'') spherical wave shown in the figure above produces an Airy disc in the image plane. The argument of the function is important, because this determines the ''scaling'' of the Airy disc (in other words, how big the disc is in the image plane). If Θmax is the maximum angle that the converging waves make with the lens axis, ''r'' is radial distance in the image plane, and wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of ...
''k'' = 2π/λ where λ = wavelength, then the argument of the function is: . If Θmax is small (only a small portion of the converging spherical wave is available to form the image), then radial distance, r, has to be very large before the total argument of the function moves away from the central spot. In other words, if Θmax is small, the Airy disc is large (which is just another statement of Heisenberg's uncertainty principle
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position a ...
for Fourier Transform pairs, namely that small extent in one domain corresponds to wide extent in the other domain, and the two are related via the '' space-bandwidth product''). By virtue of this, high magnification
Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a size ratio called optical magnification. When this number is less than one, it refers to a reduction in size, so ...
systems, which typically have small values of Θmax (by the Abbe sine condition), can have more blur in the image, owing to the broader PSF. The size of the PSF is proportional to the magnification
Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a size ratio called optical magnification. When this number is less than one, it refers to a reduction in size, so ...
, so that the blur is no worse in a relative sense, but it is definitely worse in an absolute sense.
The figure above illustrates the truncation of the incident spherical wave by the lens. In order to measure the point spread function — or impulse response function — of the lens, a perfect point source that radiates a perfect spherical wave in all directions of space is not needed. This is because the lens has only a finite (angular) bandwidth, or finite intercept angle. Therefore, any angular bandwidth contained in the source, which extends past the edge angle of the lens (i.e., lies outside the bandwidth of the system), is essentially wasted source bandwidth because the lens can't intercept it in order to process it. As a result, a perfect point source is not required in order to measure a perfect point spread function. All we need is a light source which has at least as much angular bandwidth as the lens being tested (and of course, is uniform over that angular sector). In other words, we only require a point source which is produced by a convergent (uniform) spherical wave whose half angle is greater than the edge angle of the lens.
Due to intrinsic limited resolution of the imaging systems, measured PSFs are not free of uncertainty. In imaging, it is desired to suppress the side-lobes of the imaging beam by apodization techniques. In the case of transmission imaging systems with Gaussian beam distribution, the PSF is modeled by the following equation:
:
where ''k-factor'' depends on the truncation ratio and level of the irradiance, ''NA'' is numerical aperture, ''c'' is the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
, ''f'' is the photon frequency of the imaging beam, ''Ir'' is the intensity of reference beam, ''a'' is an adjustment factor and is the radial position from the center of the beam on the corresponding ''z-plane''.
History and methods
The diffraction theory of point spread functions was first studied by Airy in the nineteenth century. He developed an expression for the point spread function amplitude and intensity of a perfect instrument, free of aberrations (the so-called Airy disc). The theory of aberrated point spread functions close to the optimum focal plane was studied by Zernike and Nijboer in the 1930–40s. A central role in their analysis is played by Zernike's circle polynomials that allow an efficient representation of the aberrations of any optical system with rotational symmetry. Recent analytic results have made it possible to extend Nijboer and Zernike's approach for point spread function evaluation to a large volume around the optimum focal point. This extended Nijboer-Zernike (ENZ) theory allows studying the imperfect imaging of three-dimensional objects inconfocal microscopy
Confocal microscopy, most frequently confocal laser scanning microscopy (CLSM) or laser scanning confocal microscopy (LSCM), is an optical imaging technique for increasing optical resolution and contrast (vision), contrast of a micrograph by me ...
or astronomy under non-ideal imaging conditions. The ENZ-theory has also been applied to the characterization of optical instruments with respect to their aberration by measuring the through-focus intensity distribution and solving an appropriate inverse problem
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, sound source reconstruction, source reconstruction in ac ...
.
Applications
Microscopy
In microscopy, experimental determination of PSF requires sub-resolution (point-like) radiating sources. Quantum dots andfluorescent
Fluorescence is one of two kinds of photoluminescence, the emission of light by a substance that has absorbed light or other electromagnetic radiation. When exposed to ultraviolet radiation, many substances will glow (fluoresce) with color ...
beads are usually considered for this purpose.
Theoretical models as described above, on the other hand, allow the detailed calculation of the PSF for various imaging conditions. The most compact diffraction limited shape of the PSF is usually preferred. However, by using appropriate optical elements (e.g., a spatial light modulator) the shape of the PSF can be engineered towards different applications.
Astronomy
 In
In observational astronomy
Observational astronomy is a division of astronomy that is concerned with recording data about the observable universe, in contrast with theoretical astronomy, which is mainly concerned with calculating the measurable implications of physical ...
, the experimental determination of a PSF is often very straightforward due to the ample supply of point sources (star
A star is a luminous spheroid of plasma (physics), plasma held together by Self-gravitation, self-gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night sk ...
s or quasars
A quasar ( ) is an extremely Luminosity, luminous active galactic nucleus (AGN). It is sometimes known as a quasi-stellar object, abbreviated QSO. The emission from an AGN is powered by accretion onto a supermassive black hole with a mass rangi ...
). The form and source of the PSF may vary widely depending on the instrument and the context in which it is used.
For radio telescopes
A radio telescope is a specialized antenna (radio), antenna and radio receiver used to detect radio waves from astronomical radio sources in the sky. Radio telescopes are the main observing instrument used in radio astronomy, which studies the r ...
and diffraction-limited space telescopes
A telescope is a device used to observe distant objects by their emission, Absorption (electromagnetic radiation), absorption, or Reflection (physics), reflection of electromagnetic radiation. Originally, it was an optical instrument using len ...
, the dominant terms in the PSF may be inferred from the configuration of the aperture in the Fourier domain. In practice, there may be multiple terms contributed by the various components in a complex optical system. A complete description of the PSF will also include diffusion of light (or photo-electrons) in the detector, as well as tracking
Tracking may refer to:
Science and technology Computing
* Tracking, in computer graphics, in match moving (insertion of graphics into footage)
* Tracking, composing music with music tracker software
* Eye tracking, measuring the position of ...
errors in the spacecraft or telescope.
For ground-based optical telescopes, atmospheric turbulence (known as astronomical seeing
In astronomy, seeing is the degradation of the real image, image of an astronomical object due to turbulence in the atmosphere of Earth that may become visible as blurring, twinkling or variable Distortion (optics), distortion. The origin of this ...
) dominates the contribution to the PSF. In high-resolution ground-based imaging, the PSF is often found to vary with position in the image (an effect called anisoplanatism). In ground-based adaptive optics
Adaptive optics (AO) is a technique of precisely deforming a mirror in order to compensate for light distortion. It is used in Astronomy, astronomical telescopes and laser communication systems to remove the effects of Astronomical seeing, atmo ...
systems, the PSF is a combination of the aperture of the system with residual uncorrected atmospheric terms.
Lithography
 The PSF is also a fundamental limit to the conventional focused imaging of a hole,The Natural Resolution
The PSF is also a fundamental limit to the conventional focused imaging of a hole,The Natural Resolution/ref> with the minimum printed size being in the range of 0.6-0.7 wavelength/NA, with NA being the
numerical aperture
In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, has the property ...
of the imaging system. For example, in the case of an EUV system with wavelength of 13.5 nm and NA=0.33, the minimum individual hole size that can be imaged is in the range of 25-29 nm. A phase-shift mask has 180-degree phase edges which allow finer resolution.
Ophthalmology
Point spread functions have recently become a useful diagnostic tool in clinicalophthalmology
Ophthalmology (, ) is the branch of medicine that deals with the diagnosis, treatment, and surgery of eye diseases and disorders.
An ophthalmologist is a physician who undergoes subspecialty training in medical and surgical eye care. Following a ...
. Patients are measured with a Shack-Hartmann wavefront sensor, and special software calculates the PSF for that patient's eye. This method allows a physician to simulate potential treatments on a patient, and estimate how those treatments would alter the patient's PSF. Additionally, once measured the PSF can be minimized using an adaptive optics system. This, in conjunction with a CCD camera and an adaptive optics system, can be used to visualize anatomical structures not otherwise visible ''in vivo'', such as cone photoreceptors.
See also
* Airy disc * Circle of confusion, for the closely related topic in general photography. * Deconvolution * Encircled energy * Impulse response function *Microscope
A microscope () is a laboratory equipment, laboratory instrument used to examine objects that are too small to be seen by the naked eye. Microscopy is the science of investigating small objects and structures using a microscope. Microscopic ...
* Microsphere
* PSF Lab
References
* * {{DEFAULTSORT:Point Spread Function Optics Ophthalmology