Planar Lamina on:
[Wikipedia]
[Google]
[Amazon]
In
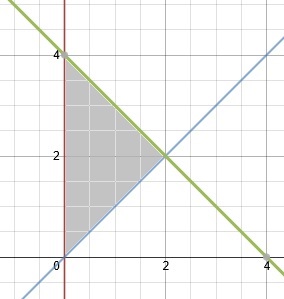 Find the center of mass of a lamina with edges given by the lines and where the density is given as .
For this the mass must be found as well as the moments and .
Mass is which can be equivalently expressed as an iterated integral:
:
The inner integral is:
:
:
:
Find the center of mass of a lamina with edges given by the lines and where the density is given as .
For this the mass must be found as well as the moments and .
Mass is which can be equivalently expressed as an iterated integral:
:
The inner integral is:
:
:
:
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a planar lamina (or plane lamina) is a figure representing a thin, usually uniform, flat layer of the solid. It serves also as an idealized model of a planar cross section of a solid body in integration.
Planar laminas can be used to determine moments of inertia, or center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d ...
of flat figures, as well as an aid in corresponding calculations for 3D bodies.
Definition
A planar lamina is defined as a figure (aclosed set
In geometry, topology, and related branches of mathematics, a closed set is a Set (mathematics), set whose complement (set theory), complement is an open set. In a topological space, a closed set can be defined as a set which contains all its lim ...
) of a finite area in a plane, with some mass .
This is useful in calculating moments of inertia or center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d ...
for a constant density, because the mass of a lamina is proportional to its area. In a case of a variable density, given by some (non-negative) surface density function the mass of the planar lamina is a planar integral of over the figure:
:
Properties
The center of mass of the lamina is at the point : where is the moment of the entire lamina about the y-axis and is the moment of the entire lamina about the x-axis: : : with summation and integration taken over a planar domain .Example
 Find the center of mass of a lamina with edges given by the lines and where the density is given as .
For this the mass must be found as well as the moments and .
Mass is which can be equivalently expressed as an iterated integral:
:
The inner integral is:
:
:
:
Find the center of mass of a lamina with edges given by the lines and where the density is given as .
For this the mass must be found as well as the moments and .
Mass is which can be equivalently expressed as an iterated integral:
:
The inner integral is:
:
:
: