pentagon tiling

In geometry, a pentagonal tiling is a tiling of the plane where each individual piece is in the shape of a pentagon.

A regular pentagonal tiling on the Euclidean plane is impossible because the internal angle of a regular pentagon, 108°, is not a divisor of 360°, the angle measure of a whole turn. However, regular pentagons can tile the hyperbolic plane with four pentagons around each vertex ( or more) and sphere with three pentagons; the latter produces a tiling that is topologically equivalent to the dodecahedron.

Monohedral convex pentagonal tilings

Fifteen types of convex pentagons are known to tile the plane monohedrally (i.e., with one type of tile). The most recent one was discovered in 2015. This list has been shown to be complete by (result subject to peer-review). showed that there are only eight edge-to-edge convex types, a result obtained independently by .

Michaël Rao of the École normale supérieure de Lyon claimed in May 2017 to have found the proof that there are in fact no convex pentagons that tile beyond these 15 types. As of 11 July 2017, the first half of Rao's proof had been independently verified (computer code available) by Thomas Hales, a professor of mathematics at the University of Pittsburgh. As of December 2017, the proof was not yet fully peer-reviewed.

Each enumerated tiling family contains pentagons that belong to no other type; however, some individual pentagons may belong to multiple types. In addition, some of the pentagons in the known tiling types also permit alternative tiling patterns beyond the standard tiling exhibited by all members of its type.

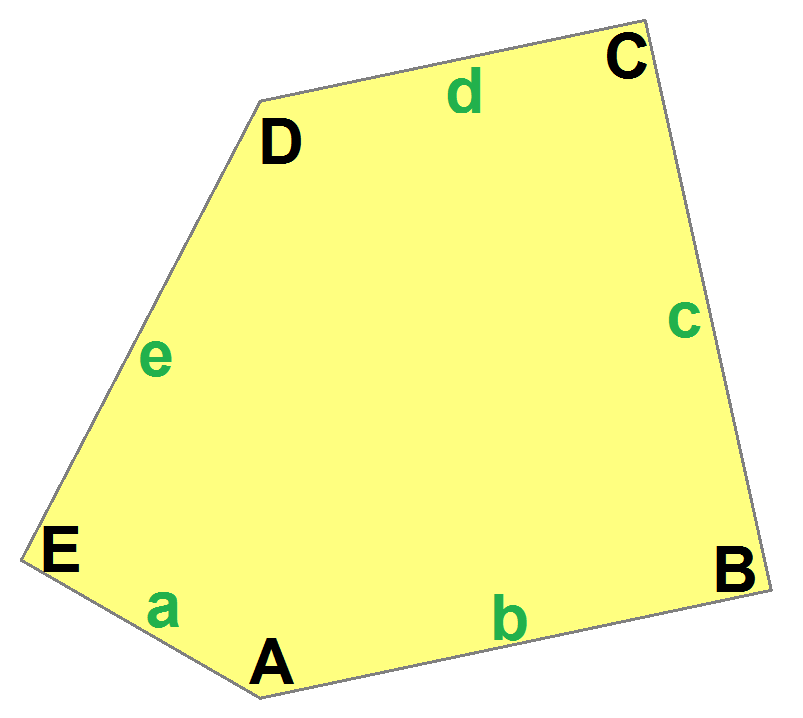
The sides of length ''a'', ''b'', ''c'', ''d'', ''e'' are directly clockwise from the angles at vertices ''A'', ''B'', ''C'', ''D'', ''E'' respectively. (Thus,
''A'', ''B'', ''C'', ''D'', ''E'' are opposite to ''d'', ''e'', ''a'', ''b'', ''c'' respectively.)

Many of these monohedral tile types have degrees of freedom. These freedoms include variations of internal angles and edge lengths. In the limit, edges may have lengths that approach zero or angles that approach 180°. Types 1, 2, 4, 5, 6, 7, 8, 9, and 13 allow parametric possibilities with nonconvex prototiles.

Periodic tilings are characterised by their wallpaper group symmetry, for example p2 (2222) is defined by four 2-fold gyration points. This nomenclature is used in the diagrams below, where the tiles are also colored by their ''k''-isohedral positions within the symmetry.

A '' primitive unit'' is a section of the tiling that generates the whole tiling using only translations, and is as small as possible.

Reinhardt (1918)

found the first five types of pentagonal tile. All five can create isohedral tilings, meaning that the symmetries of the tiling can take any tile to any other tile (more formally, the automorphism group acts transitively on the tiles).

B. Grünbaum and G. C. Shephard have shown that there are exactly twenty-four distinct "types" of isohedral tilings of the plane by pentagons according to their classification scheme. All use Reinhardt's tiles, usually with additional conditions necessary for the tiling. There are two tilings by all type 2 tiles, and one by all of each of the other four types. Fifteen of the other eighteen tilings are by special cases of type 1 tiles. Nine of the twenty-four tilings are edge-to-edge.

There are also 2-isohedral tilings by special cases of type 1, type 2, and type 4 tiles, and 3-isohedral tilings, all edge-to-edge, by special cases of type 1 tiles. There is no upper bound on k for k-isohedral tilings by certain tiles that are both type 1 and type 2, and hence neither on the number of tiles in a primitive unit.

The wallpaper group symmetry for each tiling is given, with orbifold notation in parentheses. A second lower symmetry group is given if tile chirality exists, where mirror images are considered distinct. These are shown as yellow and green tiles in those cases.

Type 1

There are many tiling topologies that contain type 1 pentagons. Five example topologies are given below.

Type 2

These type 2 examples are isohedral. The second is an edge-to-edge variation. They both have pgg (22×) symmetry. If mirror image tiles (yellow and green) are considered distinct, the symmetry is p2 (2222).

Types 3, 4, and 5

Kershner (1968) Types 6, 7, 8

found three more types of pentagonal tile, bringing the total to eight. He claimed incorrectly that this was the complete list of pentagons that can tile the plane.

These examples are 2-isohedral and edge-to-edge. Types 7 and 8 have chiral pairs of tiles, which are colored as pairs in yellow-green and the other as two shades of blue. The pgg symmetry is reduced to p2 when chiral pairs are considered distinct.

James (1975) Type 10

In 1975 Richard E. James III found a ninth type, after reading about Kershner's results in Martin Gardner's "Mathematical Games" column in ''Scientific American'' magazine of July 1975 (reprinted in ). It is indexed as type 10. The tiling is 3-isohedral and non-edge-to-edge.

Rice (1977) Types 9,11,12,13

Marjorie Rice, an amateur mathematician, discovered four new types of tessellating pentagons in 1976 and 1977.

All four tilings are 2-isohedral. The chiral pairs of tiles are colored in yellow and green for one isohedral set, and two shades of blue for the other set. The pgg symmetry is reduced to p2 when the chiral pairs are considered distinct.

The tiling by type 9 tiles is edge-to-edge, but the others are not.

Each primitive unit contains eight tiles.

Stein (1985) Type 14

A 14th convex pentagon type was found by Rolf Stein in 1985.

The tiling is 3-isohedral and non-edge-to-edge. It has completely determined tiles, with no degrees of freedom. The exact proportions are specified by $\frac = \sqrt$ and angle ''B'' obtuse with $\sin(B)=\frac$. Other relations can easily be deduced.

The primitive units contain six tiles respectively. It has p2 (2222) symmetry.

Mann/McLoud/Von Derau (2015) Type 15

University of Washington Bothell mathematicians Casey Mann, Jennifer McLoud-Mann, and David Von Derau discovered a 15th monohedral tiling convex pentagon in 2015 using a computer algorithm. It is 3-isohedral and non-edge-to-edge, drawn with 6 colors, 2 shades of 3 colors, representing chiral pairs of the three isohedral positions. The pgg symmetry is reduced to p2 when the chiral pairs are considered distinct. It has completely determined tiles, with no degrees of freedom. The primitive units contain twelve tiles. It has pgg (22×) symmetry, and p2 (2222) if chiral pairs are considered distinct.

No more periodic pentagonal tiling types

In July 2017 Michaël Rao completed a computer-assisted proof showing that there are no other types of convex pentagons that can tile the plane. The complete list of convex polygons that can tile the plane includes the above 15 pentagons, three types of hexagons, and all quadrilaterals and triangles. A consequence of this proof is that no convex polygon exists that tiles the plane only aperiodically, since all of the above types allow for a periodic tiling.

Nonperiodic monohedral pentagonal tilings

Nonperiodic monohedral pentagonal tilings can also be constructed, like the example below with 6-fold rotational symmetry by Michael Hirschhorn. Angles are A = 140°, B = 60°, C = 160°, D = 80°, E = 100°.

In 2016 Bernhard Klaassen showed that every discrete rotational symmetry type can be represented by a monohedral pentagonal tiling from the same class of pentagons. Examples for 5-fold and 7-fold symmetry are shown below. Such tilings are possible for any type of ''n''-fold rotational symmetry with ''n''>2.

Dual uniform tilings

There are three isohedral pentagonal tilings generated as duals of the uniform tilings, those with 5-valence vertices. They represent special higher symmetry cases of the 15 monohedral tilings above. Uniform tilings and their duals are all edge-to-edge. These dual tilings are also called Laves tilings. The symmetry of the uniform dual tilings is the same as the uniform tilings. Because the uniform tilings are isogonal, the duals are isohedral.

Dual ''k''-uniform tilings

The ''k''-uniform tilings with valence-5 vertices also have pentagonal dual tilings, containing the same three shaped pentagons as the semiregular duals above, but contain a mixture of pentagonal types. A ''k''-uniform tiling has a ''k''-isohedral dual tiling and are represented by different colors and shades of colors below.

For example these 2, 3, 4, and 5-uniform duals are all pentagonal:

Pentagonal/hexagonal tessellation

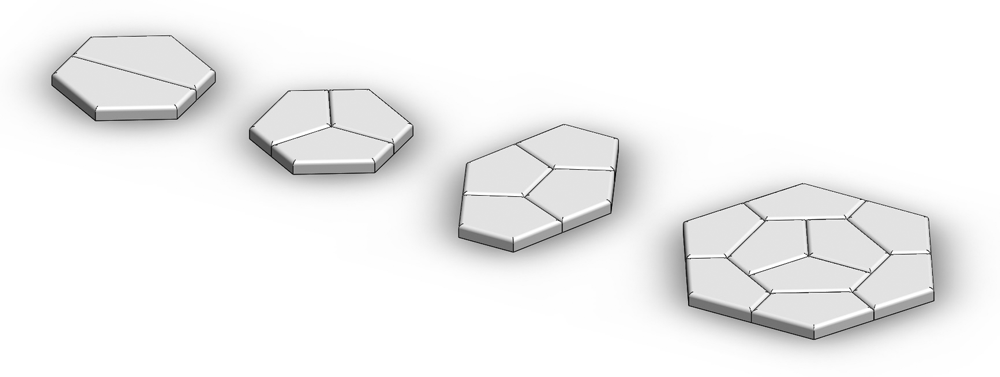
Pentagons have a peculiar relationship with hexagons. As demonstrated graphically below, some types of hexagons can be subdivided into pentagons. For example, a regular hexagon bisects into two type 1 pentagons. Subdivision of convex hexagons is also possible with three (type 3), four (type 4) and nine (type 3) pentagons.

By extension of this relation, a plane can be tessellated by a single pentagonal prototile shape in ways that generate hexagonal overlays. For example:

Non-convex pentagons

With pentagons that are not required to be convex, additional types of tiling are possible. An example is the sphinx tiling, an aperiodic tiling formed by a pentagonal rep-tile. The sphinx may also tile the plane periodically, by fitting two sphinx tiles together to form a parallelogram and then tiling the plane by translation of this parallelogram, a pattern that can be extended to any non-convex pentagon that has two consecutive angles adding to 2.

It is possible to divide an equilateral triangle into three congruent non-convex pentagons, meeting at the center of the triangle, and to tile the plane with the resulting three-pentagon unit.
A similar method can be used to subdivide squares into four congruent non-convex pentagons, or regular hexagons into six congruent non-convex pentagons, and then tile the plane with the resulting unit.

In non-Euclidean geometry

Spherical tiling

A dodecahedron can be considered a regular tiling of 12 pentagons on the surface of a sphere, with Schläfli symbol , having three pentagons around each vertex.

One may also consider a degenerate tiling by two hemispheres, with the great circle between them subdivided into five equal arcs, as a pentagonal tiling with Schläfli symbol .

Regular hyperbolic tilings

In the hyperbolic plane, one can construct regular pentagons that have any interior angle $2\pi/n$ for $n\ge 4$. The resulting pentagons tile the plane regularly, with $n$ pentagons around each vertex. For instance, the order-4 pentagonal tiling, , has four right-angled pentagons around each vertex. A limiting case is the infinite-order pentagonal tiling produced by ideal regular pentagons. These pentagons have ideal points as their vertices, with angle equal to zero.

Irregular hyperbolic tilings

There are an infinite number of dual uniform tilings in hyperbolic plane with isogonal irregular pentagonal faces. They have face configurations as V3.3.''p''.3.''q''.

A version of the binary tiling, with its tiles bounded by hyperbolic line segments rather than arcs of horocycles, forms pentagonal tilings that must be non-periodic, in the sense that their symmetry groups can be one-dimensional but not two-dimensional.

References

Bibliography

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Errata
''Forma'' 25 (1): 49, 2010,
*
*

External links

*
Pentagon Tilings15 (monohedral) Tilings with a convex pentagonal tile
with k-isohedral colorings
Code to display the 14th pentagon type tilingCode to display the 15th pentagon type tiling

{{Tessellation

Tessellation