Penrose tiling on:
[Wikipedia]
[Google]
[Amazon]
A Penrose tiling is an example of an  Penrose tilings are self-similar: they may be converted to equivalent Penrose tilings with different sizes of tiles, using processes called ''inflation'' and ''deflation''. The pattern represented by every finite patch of tiles in a Penrose tiling occurs infinitely many times throughout the tiling. They are
Penrose tilings are self-similar: they may be converted to equivalent Penrose tilings with different sizes of tiles, using processes called ''inflation'' and ''deflation''. The pattern represented by every finite patch of tiles in a Penrose tiling occurs infinitely many times throughout the tiling. They are
 Covering a flat surface ("the plane") with some pattern of geometric shapes ("tiles"), with no overlaps or gaps, is called a tiling. The most familiar tilings, such as covering a floor with squares meeting edge-to-edge, are examples of periodic tilings. If a square tiling is shifted by the width of a tile, parallel to the sides of the tile, the result is the same pattern of tiles as before the shift. A shift (formally, a
Covering a flat surface ("the plane") with some pattern of geometric shapes ("tiles"), with no overlaps or gaps, is called a tiling. The most familiar tilings, such as covering a floor with squares meeting edge-to-edge, are examples of periodic tilings. If a square tiling is shifted by the width of a tile, parallel to the sides of the tile, the result is the same pattern of tiles as before the shift. A shift (formally, a
 The subject of aperiodic tilings received new interest in the 1960s when logician Hao Wang noted connections between
The subject of aperiodic tilings received new interest in the 1960s when logician Hao Wang noted connections between  Wang's student Robert Berger proved that the Domino Problem was undecidable (so Wang's conjecture was incorrect) in his 1964 thesis, and obtained an aperiodic set of 20,426 Wang dominoes. He also described a reduction to 104 such prototiles; the latter did not appear in his published monograph, but in 1968,
Wang's student Robert Berger proved that the Domino Problem was undecidable (so Wang's conjecture was incorrect) in his 1964 thesis, and obtained an aperiodic set of 20,426 Wang dominoes. He also described a reduction to 104 such prototiles; the latter did not appear in his published monograph, but in 1968,
 Penrose subsequently reduced the number of prototiles to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below). The rhombus tiling was independently discovered by Robert Ammann in 1976. Penrose and John H. Conway investigated the properties of Penrose tilings, and discovered that a substitution property explained their hierarchical nature; their findings were publicized by
Penrose subsequently reduced the number of prototiles to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below). The rhombus tiling was independently discovered by Robert Ammann in 1976. Penrose and John H. Conway investigated the properties of Penrose tilings, and discovered that a substitution property explained their hierarchical nature; their findings were publicized by
 Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus. However, the matching rules prohibit such a combination. Both the kite and dart are composed of two triangles, called '' Robinson triangles'', after 1975 notes by Robinson.
*The ''kite'' is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
*The ''dart'' is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.
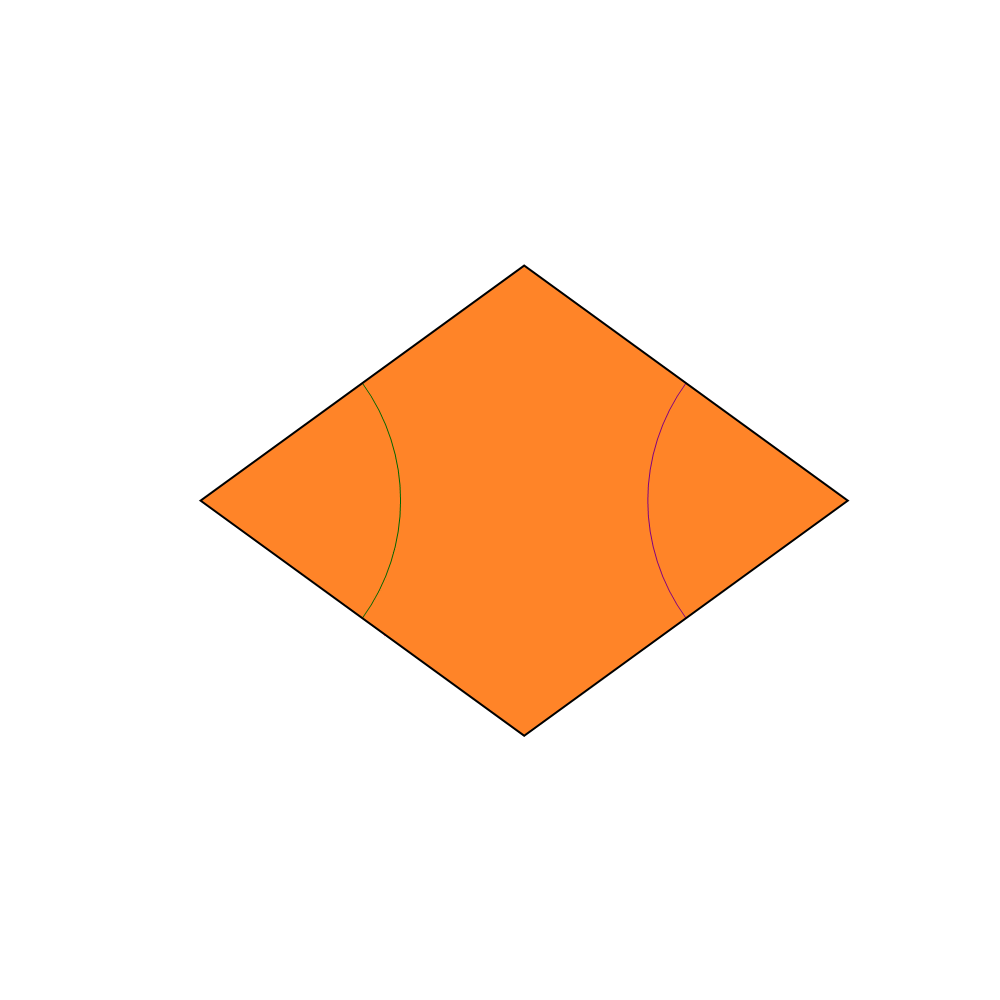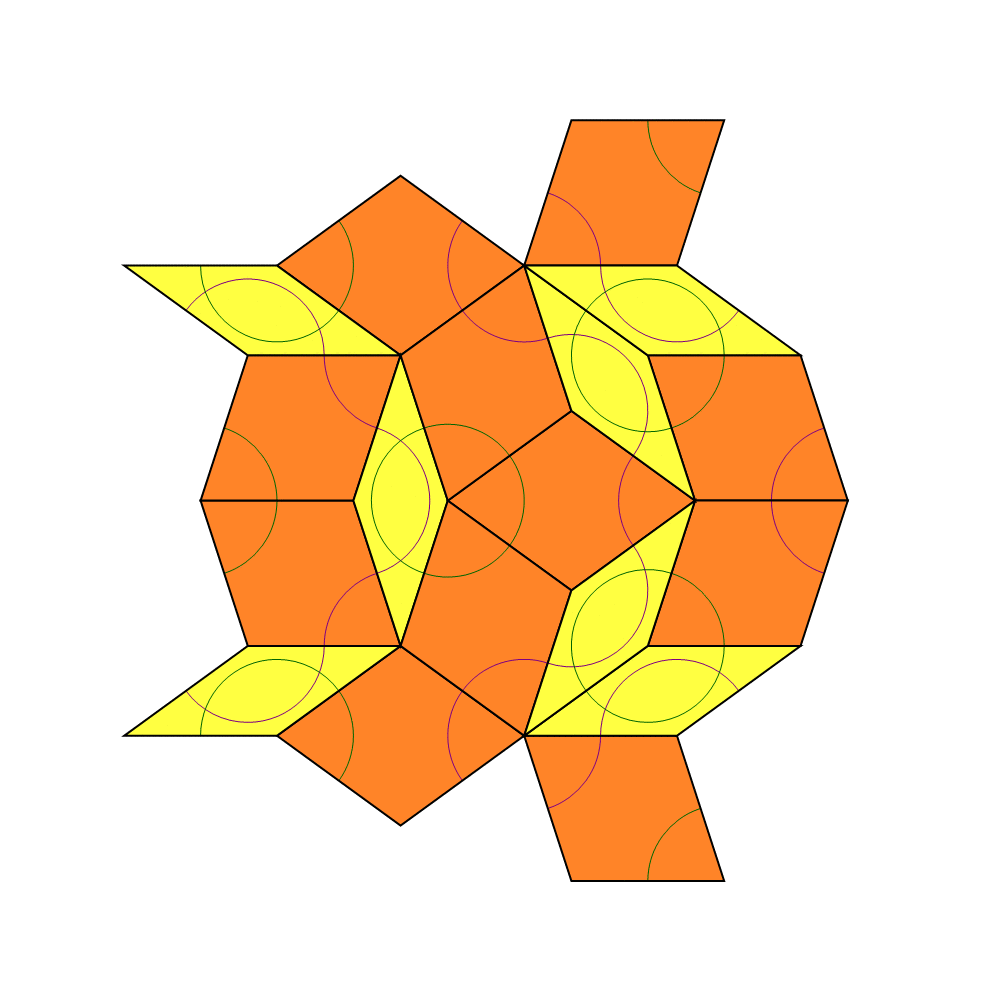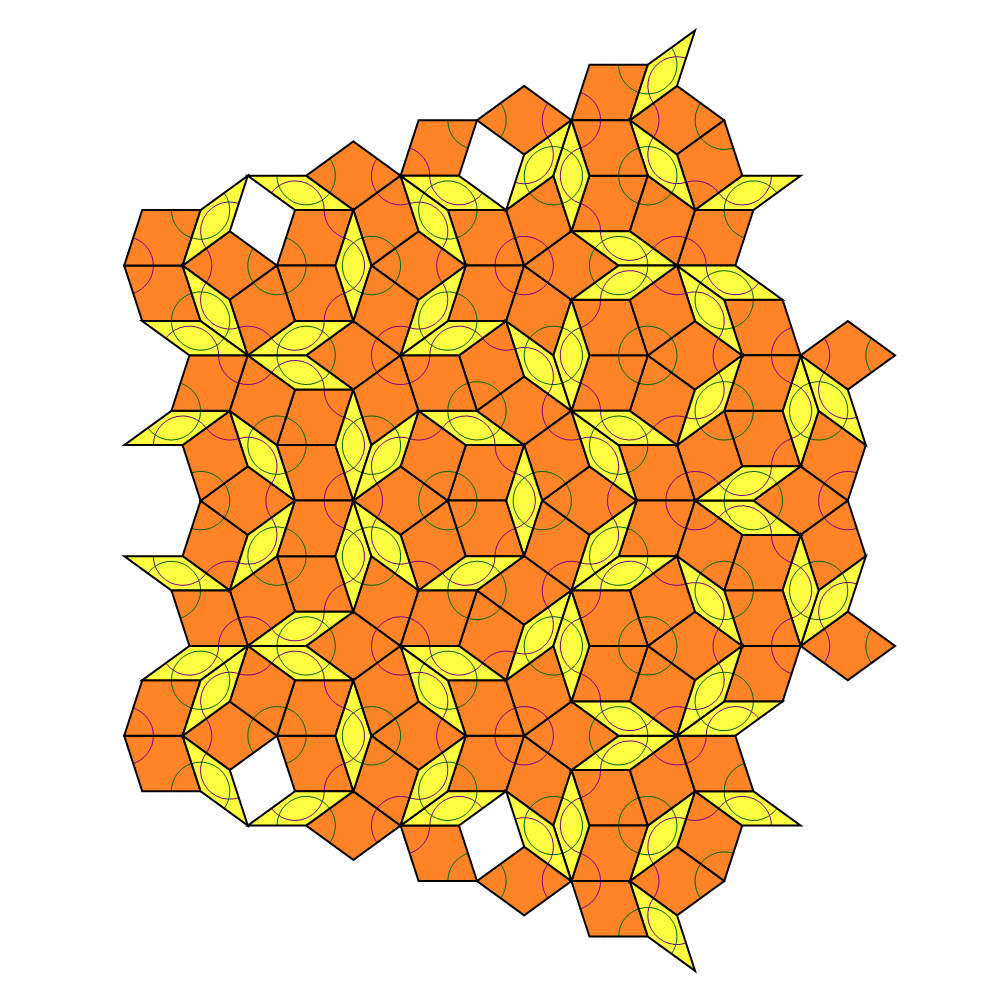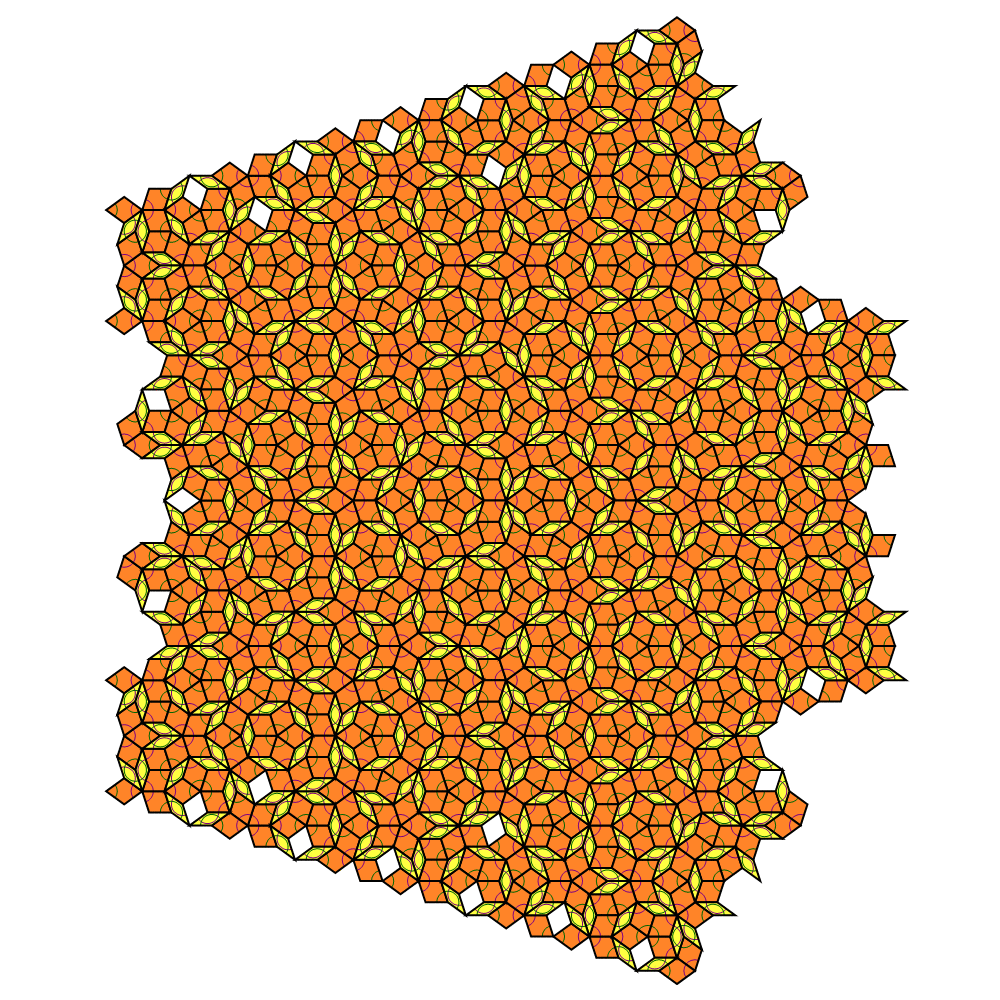
The matching rules can be described in several ways. One approach is to color the vertices (with two colors, e.g., black and white) and require that adjacent tiles have matching vertices. Another is to use a pattern of circular arcs (as shown above left in green and red) to constrain the placement of tiles: when two tiles share an edge in a tiling, the patterns must match at these edges.
These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way. Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact, there are only seven possible ways for the tiles to meet at a vertex; two of these figures – namely, the "star" (top left) and the "sun" (top right) – have 5-fold dihedral symmetry (by rotations and reflections), while the remainder have a single axis of reflection (vertical in the image). Apart from the ace (top middle) and the sun, all of these vertex figures force the placement of additional tiles.
Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus. However, the matching rules prohibit such a combination. Both the kite and dart are composed of two triangles, called '' Robinson triangles'', after 1975 notes by Robinson.
*The ''kite'' is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
*The ''dart'' is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.
The matching rules can be described in several ways. One approach is to color the vertices (with two colors, e.g., black and white) and require that adjacent tiles have matching vertices. Another is to use a pattern of circular arcs (as shown above left in green and red) to constrain the placement of tiles: when two tiles share an edge in a tiling, the patterns must match at these edges.
These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way. Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact, there are only seven possible ways for the tiles to meet at a vertex; two of these figures – namely, the "star" (top left) and the "sun" (top right) – have 5-fold dihedral symmetry (by rotations and reflections), while the remainder have a single axis of reflection (vertical in the image). Apart from the ace (top middle) and the sun, all of these vertex figures force the placement of additional tiles.


 The third tiling uses a pair of
The third tiling uses a pair of
 Consequently, the ratio of the lengths of long sides to short sides in the (
Consequently, the ratio of the lengths of long sides to short sides in the (
 Many of the common features of Penrose tilings follow from a hierarchical pentagonal structure given by '' substitution rules'': this is often referred to as ''inflation'' and ''deflation'', or ''composition'' and ''decomposition'', of tilings or (collections of) tiles.In , the term "inflation" is used where other authors would use "deflation" (followed by rescaling). The terms "composition" and "decomposition", which many authors also use, are less ambiguous. The substitution rules decompose each tile into smaller tiles of the same shape as those used in the tiling (and thus allow larger tiles to be "composed" from smaller ones). This shows that the Penrose tiling has a scaling self-similarity, and so can be thought of as a
Many of the common features of Penrose tilings follow from a hierarchical pentagonal structure given by '' substitution rules'': this is often referred to as ''inflation'' and ''deflation'', or ''composition'' and ''decomposition'', of tilings or (collections of) tiles.In , the term "inflation" is used where other authors would use "deflation" (followed by rescaling). The terms "composition" and "decomposition", which many authors also use, are less ambiguous. The substitution rules decompose each tile into smaller tiles of the same shape as those used in the tiling (and thus allow larger tiles to be "composed" from smaller ones). This shows that the Penrose tiling has a scaling self-similarity, and so can be thought of as a
 The substitution method for both P2 and P3 tilings can be described using Robinson triangles of different sizes. The Robinson triangles arising in P2 tilings (by bisecting kites and darts) are called A-tiles, while those arising in the P3 tilings (by bisecting rhombs) are called B-tiles. The smaller A-tile, denoted AS, is an obtuse Robinson triangle, while the larger A-tile, AL, is acute; in contrast, a smaller B-tile, denoted BS, is an acute Robinson triangle, while the larger B-tile, BL, is obtuse.
Concretely, if AS has side lengths (1, 1, ), then AL has side lengths (, , 1). B-tiles can be related to such A-tiles in two ways:
* If BS has the same size as AL then BL is an enlarged version AS of AS, with side lengths (, , 2 = 1 + ) – this decomposes into an AL tile and AS tile joined along a common side of length 1.
* If instead BL is identified with AS, then BS is a reduced version (1/)AL of AL with side lengths (1/,1/,1) – joining a BS tile and a BL tile along a common side of length 1 then yields (a decomposition of) an AL tile.
In these decompositions, there appears to be an ambiguity: Robinson triangles may be decomposed in two ways, which are mirror images of each other in the (isosceles) axis of symmetry of the triangle. In a Penrose tiling, this choice is fixed by the matching rules. Furthermore, the matching rules ''also'' determine how the smaller triangles in the tiling compose to give larger ones.
It follows that the P2 and P3 tilings are ''mutually locally derivable'': a tiling by one set of tiles can be used to generate a tiling by another. For example, a tiling by kites and darts may be subdivided into A-tiles, and these can be composed in a canonical way to form B-tiles and hence rhombs. The P2 and P3 tilings are also both mutually locally derivable with the P1 tiling (see figure 2 above).
The decomposition of B-tiles into A-tiles may be written
: BS = AL, BL = AL + AS
(assuming the larger size convention for the B-tiles), which can be summarized in a ''substitution
The substitution method for both P2 and P3 tilings can be described using Robinson triangles of different sizes. The Robinson triangles arising in P2 tilings (by bisecting kites and darts) are called A-tiles, while those arising in the P3 tilings (by bisecting rhombs) are called B-tiles. The smaller A-tile, denoted AS, is an obtuse Robinson triangle, while the larger A-tile, AL, is acute; in contrast, a smaller B-tile, denoted BS, is an acute Robinson triangle, while the larger B-tile, BL, is obtuse.
Concretely, if AS has side lengths (1, 1, ), then AL has side lengths (, , 1). B-tiles can be related to such A-tiles in two ways:
* If BS has the same size as AL then BL is an enlarged version AS of AS, with side lengths (, , 2 = 1 + ) – this decomposes into an AL tile and AS tile joined along a common side of length 1.
* If instead BL is identified with AS, then BS is a reduced version (1/)AL of AL with side lengths (1/,1/,1) – joining a BS tile and a BL tile along a common side of length 1 then yields (a decomposition of) an AL tile.
In these decompositions, there appears to be an ambiguity: Robinson triangles may be decomposed in two ways, which are mirror images of each other in the (isosceles) axis of symmetry of the triangle. In a Penrose tiling, this choice is fixed by the matching rules. Furthermore, the matching rules ''also'' determine how the smaller triangles in the tiling compose to give larger ones.
It follows that the P2 and P3 tilings are ''mutually locally derivable'': a tiling by one set of tiles can be used to generate a tiling by another. For example, a tiling by kites and darts may be subdivided into A-tiles, and these can be composed in a canonical way to form B-tiles and hence rhombs. The P2 and P3 tilings are also both mutually locally derivable with the P1 tiling (see figure 2 above).
The decomposition of B-tiles into A-tiles may be written
: BS = AL, BL = AL + AS
(assuming the larger size convention for the B-tiles), which can be summarized in a ''substitution

 Starting with a collection of tiles from a given tiling (which might be a single tile, a tiling of the plane, or any other collection), deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with two or more new tiles that are scaled-down versions of tiles used in the original tiling. The substitution rules guarantee that the new tiles will be arranged in accordance with the matching rules. Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.
This rule for dividing the tiles is a subdivision rule.
The above table should be used with caution. The half kite and half dart deflation are useful only in the context of deflating a larger pattern as shown in the sun and star deflations. They give incorrect results if applied to single kites and darts.
In addition, the simple subdivision rule generates holes near the edges of the tiling which are just visible in the top and bottom illustrations on the right. Additional forcing rules are useful.
Starting with a collection of tiles from a given tiling (which might be a single tile, a tiling of the plane, or any other collection), deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with two or more new tiles that are scaled-down versions of tiles used in the original tiling. The substitution rules guarantee that the new tiles will be arranged in accordance with the matching rules. Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.
This rule for dividing the tiles is a subdivision rule.
The above table should be used with caution. The half kite and half dart deflation are useful only in the context of deflating a larger pattern as shown in the sun and star deflations. They give incorrect results if applied to single kites and darts.
In addition, the simple subdivision rule generates holes near the edges of the tiling which are just visible in the top and bottom illustrations on the right. Additional forcing rules are useful.
 In 1996, German mathematician Petra Gummelt demonstrated that a covering (so called to distinguish it from a non-overlapping tiling) equivalent to the Penrose tiling can be constructed using a single decagonal tile if two kinds of overlapping regions are allowed. The decagonal tile is decorated with colored patches, and the covering rule allows only those overlaps compatible with the coloring. A suitable decomposition of the decagonal tile into kites and darts transforms such a covering into a Penrose (P2) tiling. Similarly, a P3 tiling can be obtained by inscribing a thick rhomb into each decagon; the remaining space is filled by thin rhombs.
These coverings have been considered as a realistic model for the growth of
In 1996, German mathematician Petra Gummelt demonstrated that a covering (so called to distinguish it from a non-overlapping tiling) equivalent to the Penrose tiling can be constructed using a single decagonal tile if two kinds of overlapping regions are allowed. The decagonal tile is decorated with colored patches, and the covering rule allows only those overlaps compatible with the coloring. A suitable decomposition of the decagonal tile into kites and darts transforms such a covering into a Penrose (P2) tiling. Similarly, a P3 tiling can be obtained by inscribing a thick rhomb into each decagon; the remaining space is filled by thin rhombs.
These coverings have been considered as a realistic model for the growth of
 The three variants of the Penrose tiling are mutually locally derivable. Selecting some subsets from the vertices of a P1 tiling allows to produce other non-periodic tilings. If the corners of one pentagon in P1 are labeled in succession by ''1,3,5,2,4'' an unambiguous tagging in all the pentagons is established, the order being either clockwise or counterclockwise.
Points with the same label define a tiling by Robinson triangles while points with the numbers 3 and 4 on them define the vertices of a Tie-and-Navette tiling.
The three variants of the Penrose tiling are mutually locally derivable. Selecting some subsets from the vertices of a P1 tiling allows to produce other non-periodic tilings. If the corners of one pentagon in P1 are labeled in succession by ''1,3,5,2,4'' an unambiguous tagging in all the pentagons is established, the order being either clockwise or counterclockwise.
Points with the same label define a tiling by Robinson triangles while points with the numbers 3 and 4 on them define the vertices of a Tie-and-Navette tiling.
 There are also other related unequivalent tilings, such as the hexagon-boat-star and Mikulla–Roth tilings. For instance, if the matching rules for the rhombus tiling are reduced to a specific restriction on the angles permitted at each vertex, a binary tiling is obtained. Its underlying symmetry is also fivefold but it is not a quasicrystal. It can be obtained either by decorating the rhombs of the original tiling with smaller ones, or by applying substitution rules, but not by de Bruijn's cut-and-project method.
There are also other related unequivalent tilings, such as the hexagon-boat-star and Mikulla–Roth tilings. For instance, if the matching rules for the rhombus tiling are reduced to a specific restriction on the angles permitted at each vertex, a binary tiling is obtained. Its underlying symmetry is also fivefold but it is not a quasicrystal. It can be obtained either by decorating the rhombs of the original tiling with smaller ones, or by applying substitution rules, but not by de Bruijn's cut-and-project method.
File:Darb-i Imam shrine spandrel.JPG, Pentagonal and decagonal Girih-tile pattern on a
The aesthetic value of tilings has long been appreciated, and remains a source of interest in them; hence the visual appearance (rather than the formal defining properties) of Penrose tilings has attracted attention. The similarity with certain decorative patterns used in North Africa and the Middle East has been noted; the physicists Peter J. Lu and
aperiodic tiling
An aperiodic tiling is a non-periodic Tessellation, tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. A set of tile-types (or prototiles) is aperiodic set of prototiles, aperiodic if copie ...
. Here, a ''tiling'' is a covering of the plane by non-overlapping polygons or other shapes, and a tiling is ''aperiodic'' if it does not contain arbitrarily large periodic regions or patches. However, despite their lack of translational symmetry
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation (without rotation). Discrete translational symmetry is invariant under discrete translation.
Analogously, an operato ...
, Penrose tilings may have both reflection symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a Reflection (mathematics), reflection. That is, a figure which does not change upon undergoing a reflection has reflecti ...
and fivefold rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape (geometry), shape has when it looks the same after some rotation (mathematics), rotation by a partial turn (angle), turn. An object's degree of rotational s ...
. Penrose tilings are named after mathematician and physicist Roger Penrose
Sir Roger Penrose (born 8 August 1931) is an English mathematician, mathematical physicist, Philosophy of science, philosopher of science and Nobel Prize in Physics, Nobel Laureate in Physics. He is Emeritus Rouse Ball Professor of Mathematics i ...
, who investigated them in the 1970s.
There are several variants of Penrose tilings with different tile shapes. The original form of Penrose tiling used tiles of four different shapes, but this was later reduced to only two shapes: either two different rhombi
In plane Euclidean geometry, a rhombus (: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhom ...
, or two different quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''l ...
s called kites
A kite is a tethered heavier than air flight, heavier-than-air craft with wing surfaces that react against the air to create Lift (force), lift and Drag (physics), drag forces. A kite consists of wings, tethers and anchors. Kites often have ...
and darts. The Penrose tilings are obtained by constraining the ways in which these shapes are allowed to fit together in a way that avoids periodic tiling. This may be done in several different ways, including matching rules, substitution tiling or finite subdivision rule
In mathematics, a finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. Subdivision rules in a sense are generalizations of regular geometric fractals. Instead of repeati ...
s, cut and project schemes, and coverings. Even constrained in this manner, each variation yields infinitely many different Penrose tilings.
 Penrose tilings are self-similar: they may be converted to equivalent Penrose tilings with different sizes of tiles, using processes called ''inflation'' and ''deflation''. The pattern represented by every finite patch of tiles in a Penrose tiling occurs infinitely many times throughout the tiling. They are
Penrose tilings are self-similar: they may be converted to equivalent Penrose tilings with different sizes of tiles, using processes called ''inflation'' and ''deflation''. The pattern represented by every finite patch of tiles in a Penrose tiling occurs infinitely many times throughout the tiling. They are quasicrystal
A quasiperiodicity, quasiperiodic crystal, or quasicrystal, is a structure that is Order and disorder (physics), ordered but not Bravais lattice, periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks trans ...
s: implemented as a physical structure a Penrose tiling will produce diffraction patterns with Bragg peaks and five-fold symmetry, revealing the repeated patterns and fixed orientations of its tiles. The study of these tilings has been important in the understanding of physical materials that also form quasicrystals. Penrose tilings have also been applied in architecture and decoration, as in the floor tiling shown.
The 2011 Nobel Prize in Chemistry was awarded for "The Discovery of Quasicrystals." Penrose tiling was mentioned for having "'helped pave the way for the understanding of the discovery of quasicrystals.'"
Background and history
Periodic and aperiodic tilings
translation
Translation is the communication of the semantics, meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The English la ...
) that preserves the tiling in this way is called a ''period'' of the tiling. A tiling is called periodic when it has periods that shift the tiling in two different directions.General references for this article include , , and .
The tiles in the square tiling have only one shape, and it is common for other tilings to have only a finite number of shapes. These shapes are called '' prototiles'', and a set of prototiles is said to ''admit a tiling'' or ''tile the plane'' if there is a tiling of the plane using only these shapes. That is, each tile in the tiling must be congruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
to one of these prototiles.
A tiling that has no periods is ''non-periodic''. A set of prototiles is said to be ''aperiodic'' if all of its tilings are non-periodic, and in this case its tilings are also called aperiodic tiling
An aperiodic tiling is a non-periodic Tessellation, tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. A set of tile-types (or prototiles) is aperiodic set of prototiles, aperiodic if copie ...
s. Penrose tilings are among the simplest known examples of aperiodic tilings of the plane by finite sets of prototiles.
Earliest aperiodic tilings
decision problem
In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question on a set of input values. An example of a decision problem is deciding whether a given natura ...
s and tilings. In particular, he introduced tilings by square plates with colored edges, now known as '' Wang dominoes'' or ''tiles'', and posed the "'' Domino Problem''": to determine whether a given set of Wang dominoes could tile the plane with matching colors on adjacent domino edges. He observed that if this problem were undecidable, then there would have to exist an aperiodic set of Wang dominoes. At the time, this seemed implausible, so Wang conjectured no such set could exist.
Donald Knuth
Donald Ervin Knuth ( ; born January 10, 1938) is an American computer scientist and mathematician. He is a professor emeritus at Stanford University. He is the 1974 recipient of the ACM Turing Award, informally considered the Nobel Prize of comp ...
detailed a modification of Berger's set requiring only 92 dominoes.
The color matching required in a tiling by Wang dominoes can easily be achieved by modifying the edges of the tiles like jigsaw puzzle
A jigsaw puzzle (with context, sometimes just jigsaw or just puzzle) is a tiling puzzle that requires the assembly of often irregularly shaped interlocking and mosaicked pieces. Typically each piece has a portion of a picture, which is comple ...
pieces so that they can fit together only as prescribed by the edge colorings. Raphael Robinson, in a 1971 paper which simplified Berger's techniques and undecidability proof, used this technique to obtain an aperiodic set of just six prototiles.
Development of the Penrose tilings
The first Penrose tiling (tiling P1 below) is an aperiodic set of six prototiles, introduced byRoger Penrose
Sir Roger Penrose (born 8 August 1931) is an English mathematician, mathematical physicist, Philosophy of science, philosopher of science and Nobel Prize in Physics, Nobel Laureate in Physics. He is Emeritus Rouse Ball Professor of Mathematics i ...
in a 1974 paper, based on pentagons rather than squares. Any attempt to tile the plane with regular pentagons necessarily leaves gaps, but Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
showed, in his 1619 work ''Harmonices Mundi
''Harmonice Mundi'' (Latin: ''The Harmony of the World'', 1619) is a book by Johannes Kepler. In the work, written entirely in Latin, Kepler discusses harmony and congruence in geometrical forms and physical phenomena. The final section of t ...
'', that these gaps can be filled using pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle around ...
s (star polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, Decagram (geometry)#Related figures, certain notable ones can ...
s), decagons and related shapes. Kepler extended this tiling by five polygons and found no periodic patterns, and already conjectured that every extension would introduce a new feature hence creating an aperiodic tiling. Traces of these ideas can also be found in the work of Albrecht Dürer
Albrecht Dürer ( , ;; 21 May 1471 – 6 April 1528),Müller, Peter O. (1993) ''Substantiv-Derivation in Den Schriften Albrecht Dürers'', Walter de Gruyter. . sometimes spelled in English as Durer or Duerer, was a German painter, Old master prin ...
. Acknowledging inspiration from Kepler, Penrose found matching rules for these shapes, obtaining an aperiodic set. These matching rules can be imposed by decorations of the edges, as with the Wang tiles. Penrose's tiling can be viewed as a completion of Kepler's finite ''Aa'' pattern.
 Penrose subsequently reduced the number of prototiles to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below). The rhombus tiling was independently discovered by Robert Ammann in 1976. Penrose and John H. Conway investigated the properties of Penrose tilings, and discovered that a substitution property explained their hierarchical nature; their findings were publicized by
Penrose subsequently reduced the number of prototiles to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below). The rhombus tiling was independently discovered by Robert Ammann in 1976. Penrose and John H. Conway investigated the properties of Penrose tilings, and discovered that a substitution property explained their hierarchical nature; their findings were publicized by Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing magic, scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writin ...
in his January 1977 "Mathematical Games
A mathematical game is a game whose rules, strategies, and outcomes are defined by clear mathematics, mathematical parameters. Often, such games have simple rules and match procedures, such as tic-tac-toe and dots and boxes. Generally, mathemati ...
" column in ''Scientific American
''Scientific American'', informally abbreviated ''SciAm'' or sometimes ''SA'', is an American popular science magazine. Many scientists, including Albert Einstein and Nikola Tesla, have contributed articles to it, with more than 150 Nobel Pri ...
''.
In 1981, N. G. de Bruijn provided two different methods to construct Penrose tilings. De Bruijn's "multigrid method" obtains the Penrose tilings as the dual graph
In the mathematics, mathematical discipline of graph theory, the dual graph of a planar graph is a graph that has a vertex (graph theory), vertex for each face (graph theory), face of . The dual graph has an edge (graph theory), edge for each p ...
s of arrangements
In music, an arrangement is a musical adaptation of an existing Composition (music), composition. Differences from the original composition may include Harmony (music), reharmonization, Musical phrasing, melodic paraphrasing, orchestration, or M ...
of five families of parallel lines. In his "cut and project method", Penrose tilings are obtained as two-dimensional projections from a five-dimensional cubic structure. In these approaches, the Penrose tiling is viewed as a set of points, its vertices, while the tiles are geometrical shapes obtained by connecting vertices with edges. A 1990 construction by Baake, Kramer, Schlottmann, and Zeidler derived the Penrose tiling and the related Tübingen triangle tiling in a similar manner from the four-dimensional 5-cell honeycomb.
Penrose tilings
The three types of Penrose tiling, P1–P3, are described individually below.The P1–P3 notation is taken from They have many common features: in each case, the tiles are constructed from shapes related to the pentagon (and hence to thegolden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
), but the basic tile shapes need to be supplemented by ''matching rules'' in order to tile aperiodically. These rules may be described using labeled vertices or edges, or patterns on the tile faces; alternatively, the edge profile can be modified (e.g. by indentations and protrusions) to obtain an aperiodic set of prototiles.
Original pentagonal Penrose tiling (P1)
Penrose's first tiling uses pentagons and three other shapes: a five-pointed "star" (a pentagram), a "boat" (roughly 3/5 of a star) and a "diamond" (a thin rhombus). To ensure that all tilings are non-periodic, there are that specify how tiles may meet each other, and there are three different types of matching rule for the pentagonal tiles. Treating these three types as different prototiles gives a set of six prototiles overall. It is common to indicate the three different types of pentagonal tiles using three different colors, as in the figure above right.Kite and dart tiling (P2)
 Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus. However, the matching rules prohibit such a combination. Both the kite and dart are composed of two triangles, called '' Robinson triangles'', after 1975 notes by Robinson.
*The ''kite'' is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
*The ''dart'' is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.
The matching rules can be described in several ways. One approach is to color the vertices (with two colors, e.g., black and white) and require that adjacent tiles have matching vertices. Another is to use a pattern of circular arcs (as shown above left in green and red) to constrain the placement of tiles: when two tiles share an edge in a tiling, the patterns must match at these edges.
These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way. Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact, there are only seven possible ways for the tiles to meet at a vertex; two of these figures – namely, the "star" (top left) and the "sun" (top right) – have 5-fold dihedral symmetry (by rotations and reflections), while the remainder have a single axis of reflection (vertical in the image). Apart from the ace (top middle) and the sun, all of these vertex figures force the placement of additional tiles.
Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus. However, the matching rules prohibit such a combination. Both the kite and dart are composed of two triangles, called '' Robinson triangles'', after 1975 notes by Robinson.
*The ''kite'' is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
*The ''dart'' is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.
The matching rules can be described in several ways. One approach is to color the vertices (with two colors, e.g., black and white) and require that adjacent tiles have matching vertices. Another is to use a pattern of circular arcs (as shown above left in green and red) to constrain the placement of tiles: when two tiles share an edge in a tiling, the patterns must match at these edges.
These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way. Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact, there are only seven possible ways for the tiles to meet at a vertex; two of these figures – namely, the "star" (top left) and the "sun" (top right) – have 5-fold dihedral symmetry (by rotations and reflections), while the remainder have a single axis of reflection (vertical in the image). Apart from the ace (top middle) and the sun, all of these vertex figures force the placement of additional tiles.
Rhombus tiling (P3)
 The third tiling uses a pair of
The third tiling uses a pair of rhombus
In plane Euclidean geometry, a rhombus (: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhom ...
es (often referred to as " rhombs" in this context) with equal sides but different angles. Ordinary rhombus-shaped tiles can be used to tile the plane periodically, so restrictions must be made on how tiles can be assembled: no two tiles may form a parallelogram, as this would allow a periodic tiling, but this constraint is not sufficient to force aperiodicity, as figure 1 above shows.
There are two kinds of tile, both of which can be decomposed into Robinson triangles.
*The thin rhomb t has four corners with angles of 36, 144, 36, and 144 degrees. The t rhomb may be bisected along its short diagonal to form a pair of acute Robinson triangles.
*The thick rhomb T has angles of 72, 108, 72, and 108 degrees. The T rhomb may be bisected along its long diagonal to form a pair of obtuse Robinson triangles; in contrast to the P2 tiling, these are larger than the acute triangles.
The matching rules distinguish sides of the tiles, and entail that tiles may be juxtaposed in certain particular ways but not in others. Two ways to describe these matching rules are shown in the image on the right. In one form, tiles must be assembled such that the curves on the faces match in color and position across an edge. In the other, tiles must be assembled such that the bumps on their edges fit together.
There are 54 cyclically ordered combinations of such angles that add up to 360 degrees at a vertex, but the rules of the tiling allow only seven of these combinations to appear (although one of these arises in two ways).
The various combinations of angles and facial curvature allow construction of arbitrarily complex tiles, such as the ''Penrose chickens''.
Features and constructions
Golden ratio and local pentagonal symmetry
Several properties and common features of the Penrose tilings involve thegolden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
(approximately 1.618). This is the ratio of chord lengths to side lengths in a regular pentagon
In geometry, a pentagon () is any five-sided polygon or 5-gon. The sum of the internal angles in a simple polygon, simple pentagon is 540°.
A pentagon may be simple or list of self-intersecting polygons, self-intersecting. A self-intersecting ...
, and satisfies = 1 + 1/.
isosceles
In geometry, an isosceles triangle () is a triangle that has two sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides ...
) Robinson triangles is :1. It follows that the ratio of long side lengths to short in both kite and dart tiles is also :1, as are the length ratios of sides to the short diagonal in the thin rhomb t, and of long diagonal to sides in the thick rhomb T. In both the P2 and P3 tilings, the ratio of the area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-di ...
of the larger Robinson triangle to the smaller one is :1, hence so are the ratios of the areas of the kite to the dart, and of the thick rhomb to the thin rhomb. (Both larger and smaller obtuse Robinson triangles can be found in the pentagon on the left: the larger triangles at the top – the halves of the thick rhomb – have linear dimensions scaled up by compared to the small shaded triangle at the base, and so the ratio of areas is 2:1.)
Any Penrose tiling has local pentagonal symmetry, in the sense that there are points in the tiling surrounded by a symmetric configuration of tiles: such configurations have fivefold rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape (geometry), shape has when it looks the same after some rotation (mathematics), rotation by a partial turn (angle), turn. An object's degree of rotational s ...
about the center point, as well as five mirror lines of reflection symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a Reflection (mathematics), reflection. That is, a figure which does not change upon undergoing a reflection has reflecti ...
passing through the point, a dihedral symmetry group
A group is a number of persons or things that are located, gathered, or classed together.
Groups of people
* Cultural group, a group whose members share the same cultural identity
* Ethnic group, a group whose members share the same ethnic iden ...
. This symmetry will generally preserve only a patch of tiles around the center point, but the patch can be very large: Conway and Penrose proved that whenever the colored curves on the P2 or P3 tilings close in a loop, the region within the loop has pentagonal symmetry, and furthermore, in any tiling, there are at most two such curves of each color that do not close up.
There can be at most one center point of global fivefold symmetry: if there were more than one, then rotating each about the other would yield two closer centers of fivefold symmetry, which leads to a mathematical contradiction. There are only two Penrose tilings (of each type) with global pentagonal symmetry: for the P2 tiling by kites and darts, the center point is either a "sun" or "star" vertex.
Inflation and deflation
fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
, using the same process as the pentaflake.
Penrose originally discovered the P1 tiling in this way, by decomposing a pentagon into six smaller pentagons (one half of a net of a dodecahedron
In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Po ...
) and five half-diamonds; he then observed that when he repeated this process the gaps between pentagons could all be filled by stars, diamonds, boats and other pentagons. By iterating this process indefinitely he obtained one of the two P1 tilings with pentagonal symmetry.
Robinson triangle decompositions
matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
'' equation:
:
Combining this with the decomposition of enlarged A-tiles into B-tiles yields the substitution
:
so that the enlarged tile AL decomposes into two AL tiles and one AS tiles. The matching rules force a particular substitution: the two AL tiles in a AL tile must form a kite, and thus a kite decomposes into two kites and a two half-darts, and a dart decomposes into a kite and two half-darts. Enlarged B-tiles decompose into B-tiles in a similar way (via A-tiles).
Composition and decomposition can be iterated, so that, for example
:
The number of kites and darts in the ''n''th iteration of the construction is determined by the ''n''th power of the substitution matrix:
:
where ''F''''n'' is the ''n''th Fibonacci number
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many w ...
. The ratio of numbers of kites to darts in any sufficiently large P2 Penrose tiling pattern therefore approximates to the golden ratio . A similar result holds for the ratio of the number of thick rhombs to thin rhombs in the P3 Penrose tiling.
Deflation for P2 and P3 tilings


 Starting with a collection of tiles from a given tiling (which might be a single tile, a tiling of the plane, or any other collection), deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with two or more new tiles that are scaled-down versions of tiles used in the original tiling. The substitution rules guarantee that the new tiles will be arranged in accordance with the matching rules. Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.
This rule for dividing the tiles is a subdivision rule.
The above table should be used with caution. The half kite and half dart deflation are useful only in the context of deflating a larger pattern as shown in the sun and star deflations. They give incorrect results if applied to single kites and darts.
In addition, the simple subdivision rule generates holes near the edges of the tiling which are just visible in the top and bottom illustrations on the right. Additional forcing rules are useful.
Starting with a collection of tiles from a given tiling (which might be a single tile, a tiling of the plane, or any other collection), deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with two or more new tiles that are scaled-down versions of tiles used in the original tiling. The substitution rules guarantee that the new tiles will be arranged in accordance with the matching rules. Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.
This rule for dividing the tiles is a subdivision rule.
The above table should be used with caution. The half kite and half dart deflation are useful only in the context of deflating a larger pattern as shown in the sun and star deflations. They give incorrect results if applied to single kites and darts.
In addition, the simple subdivision rule generates holes near the edges of the tiling which are just visible in the top and bottom illustrations on the right. Additional forcing rules are useful.
Consequences and applications
Inflation and deflation yield a method for constructing kite and dart (P2) tilings, or rhombus (P3) tilings, known as ''up-down generation''. The Penrose tilings, being non-periodic, have no translational symmetry – the pattern cannot be shifted to match itself over the entire plane. However, any bounded region, no matter how large, will be repeated an infinite number of times within the tiling. Therefore, no finite patch can uniquely determine a full Penrose tiling, nor even determine which position within the tiling is being shown. This shows in particular that the number of distinct Penrose tilings (of any type) isuncountably infinite
In mathematics, an uncountable set, informally, is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger tha ...
. Up-down generation yields one method to parameterize the tilings, but other methods use Ammann bars, pentagrids, or cut and project schemes.
Related tilings and topics
Decagonal coverings and quasicrystals
quasicrystals
A quasiperiodicity, quasiperiodic crystal, or quasicrystal, is a structure that is Order and disorder (physics), ordered but not Bravais lattice, periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks trans ...
: the overlapping decagons are 'quasi-unit cells' analogous to the unit cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector
In mathematics, a unit vector i ...
s from which crystals are constructed, and the matching rules maximize the density of certain atomic clusters. The aperiodic nature of the coverings can make theoretical studies of physical properties, such as electronic structure, difficult due to the absence of Bloch's theorem. However, spectra of quasicrystals can still be computed with error control.
Related tilings
 The three variants of the Penrose tiling are mutually locally derivable. Selecting some subsets from the vertices of a P1 tiling allows to produce other non-periodic tilings. If the corners of one pentagon in P1 are labeled in succession by ''1,3,5,2,4'' an unambiguous tagging in all the pentagons is established, the order being either clockwise or counterclockwise.
Points with the same label define a tiling by Robinson triangles while points with the numbers 3 and 4 on them define the vertices of a Tie-and-Navette tiling.
The three variants of the Penrose tiling are mutually locally derivable. Selecting some subsets from the vertices of a P1 tiling allows to produce other non-periodic tilings. If the corners of one pentagon in P1 are labeled in succession by ''1,3,5,2,4'' an unambiguous tagging in all the pentagons is established, the order being either clockwise or counterclockwise.
Points with the same label define a tiling by Robinson triangles while points with the numbers 3 and 4 on them define the vertices of a Tie-and-Navette tiling.
Art and architecture
spandrel
A spandrel is a roughly triangular space, usually found in pairs, between the top of an arch and a rectangular frame, between the tops of two adjacent arches, or one of the four spaces between a circle within a square. They are frequently fil ...
from the Darb-i Imam shrine, Isfahan
Isfahan or Esfahan ( ) is a city in the Central District (Isfahan County), Central District of Isfahan County, Isfahan province, Iran. It is the capital of the province, the county, and the district. It is located south of Tehran. The city ...
, Iran
Iran, officially the Islamic Republic of Iran (IRI) and also known as Persia, is a country in West Asia. It borders Iraq to the west, Turkey, Azerbaijan, and Armenia to the northwest, the Caspian Sea to the north, Turkmenistan to the nort ...
(1453 C.E.)
File:Salesforce Transit Center main entrance.jpg, Salesforce Transit Center in San Francisco. The outer "skin", made of white aluminum, is perforated in the pattern of a Penrose tiling.
File:Penrose tiling in CC-3, IIIT Allahabad.jpg, alt=, Penrose tiling on the floor in Computer Center 3 (CC-3), IIIT Allahabad
Paul Steinhardt
Paul Joseph Steinhardt (born December 25, 1952) is an American theoretical physicist whose principal research is in cosmology and condensed matter physics. He is currently the Albert Einstein Professorship in Science, Albert Einstein Professor in ...
have presented evidence that a Penrose tiling underlies examples of medieval Islamic geometric patterns
Islamic geometric patterns are one of the major forms of Islamic ornament, which tends to avoid using figurative art, figurative images, as it is forbidden to create a representation of an important Islamic figure according to many Quran, holy ...
, such as the girih (strapwork) tilings at the Darb-e Imam
The Darb-e Imam (; ) is a Twelver Shi'ite Imamzadeh complex located in the Dardasht quarter of Esfahan, in the province of Isfahan, Iran. The complex comprises two shrines, a mosque, a mausoleum, and a royal cemetery.
The complex was added ...
shrine in Isfahan
Isfahan or Esfahan ( ) is a city in the Central District (Isfahan County), Central District of Isfahan County, Isfahan province, Iran. It is the capital of the province, the county, and the district. It is located south of Tehran. The city ...
.
Artist Clark Richert used the same rhombs in artwork he was developing at Drop City in 1970 which he derived by projecting the rhombic triacontahedron shadow onto a plane and observing the embedded "fat" rhombi and "skinny" rhombi which tile together to produce the non-periodic tessellation, predating Penrose's discovery. These geometric explorations led to the development of Steve Baer's Zome Architecture. Art historian Martin Kemp has observed that Albrecht Dürer
Albrecht Dürer ( , ;; 21 May 1471 – 6 April 1528),Müller, Peter O. (1993) ''Substantiv-Derivation in Den Schriften Albrecht Dürers'', Walter de Gruyter. . sometimes spelled in English as Durer or Duerer, was a German painter, Old master prin ...
sketched similar motifs of a rhombus tiling.
In 1979, Miami University
Miami University (informally Miami of Ohio or simply Miami) is a public university, public research university in Oxford, Ohio, United States. Founded in 1809, it is the second-oldest List of colleges and universities in Ohio, university in Ohi ...
used a Penrose tiling executed in terrazzo
Terrazzo is a composite material, poured in place or precast, which is used for floor and wall treatments. It consists of chips of marble, quartz, granite, glass, or other suitable material, poured with a cementitious binder (for chemical bind ...
to decorate the Bachelor Hall courtyard in their Department of Mathematics and Statistics.
In Indian Institute of Information Technology, Allahabad, since the first phase of construction in 2001, academic buildings were designed on the basis of "Penrose Geometry", styled on tessellations
A tessellation or tiling is the covering of a surface, often a plane (mathematics), plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to high-dimensiona ...
developed by Roger Penrose. In many places in those buildings, the floor has geometric patterns composed of Penrose tiling.
The floor of the atrium of the Bayliss Building at The University of Western Australia is tiled with Penrose tiles.
The Andrew Wiles
Sir Andrew John Wiles (born 11 April 1953) is an English mathematician and a Royal Society Research Professor at the University of Oxford, specialising in number theory. He is best known for Wiles's proof of Fermat's Last Theorem, proving Ferma ...
Building, the location of the Mathematics Department at the University of Oxford
The University of Oxford is a collegiate university, collegiate research university in Oxford, England. There is evidence of teaching as early as 1096, making it the oldest university in the English-speaking world and the List of oldest un ...
as of October 2013, includes a section of Penrose tiling as the paving of its entrance.
The pedestrian part of the street Keskuskatu in central Helsinki is paved using a form of Penrose tiling. The work was finished in 2014.
San Francisco's 2018 Salesforce Transit Center features perforations in its exterior's undulating white metal skin in the Penrose pattern.
See also
* Girih tiles * List of aperiodic sets of tiles * Pinwheel tiling * Pentagonal tiling * Quaquaversal tiling * Tübingen triangleNotes
References
Primary sources
* . * . * * . * . * . * * .Secondary sources
* . * . * * * . (First published by W. H. Freeman, New York (1989), .) **Chapter 1 (pp. 1–18) is a reprint of . * . * . * . * . * * . * . * . * . (Page numbers cited here are from the reproduction as .) * * . * . * .External links
* * * * * * This has a list of additional resources. * * {{DEFAULTSORT:Penrose Tiling Discrete geometry Aperiodic tilings Mathematics and art Golden ratio Roger Penrose