Pencil Of Parallel Lines on:
[Wikipedia]
[Google]
[Amazon]
 In
In
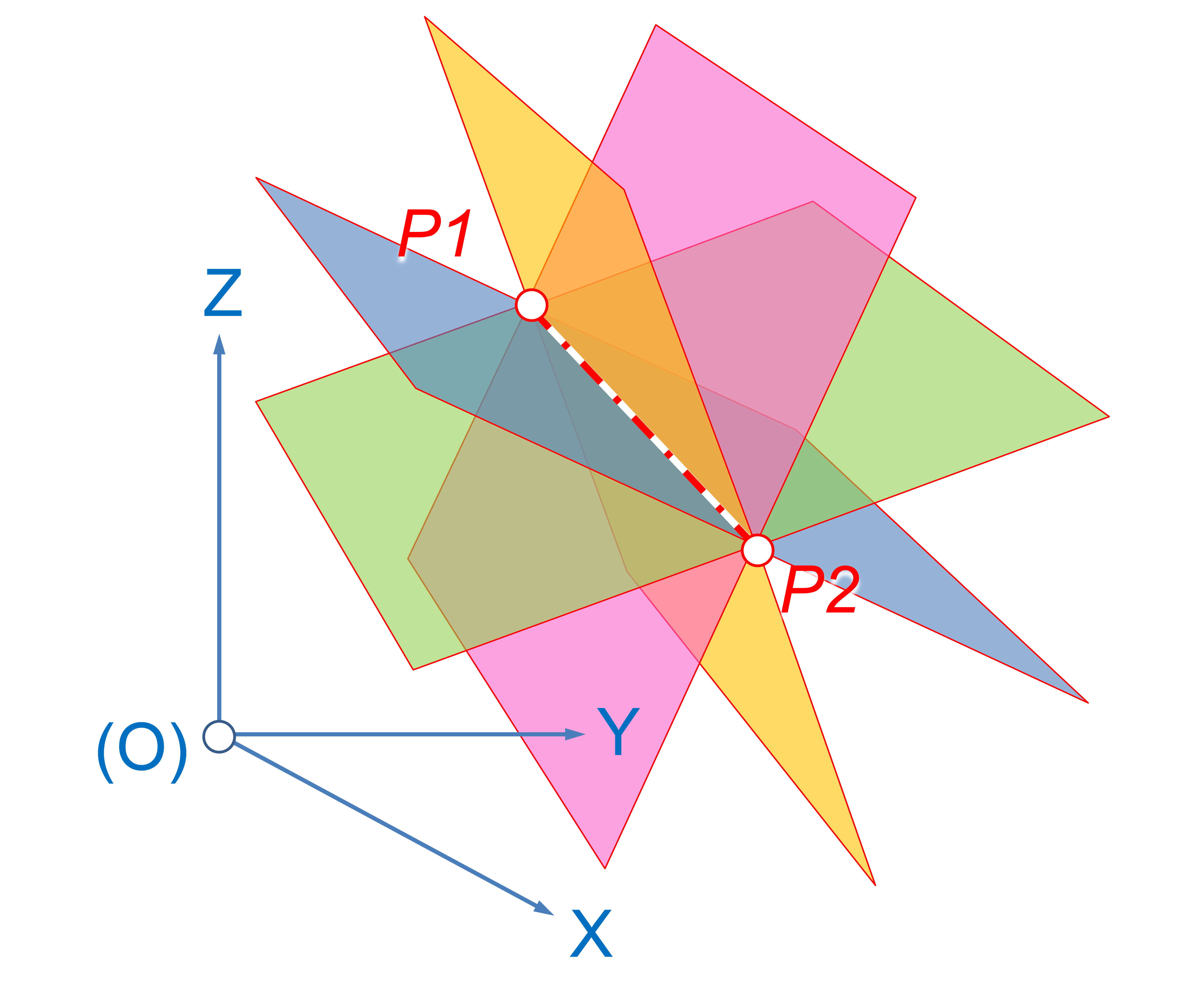 A pencil of planes, is the set of planes through a given straight line in three-space, called the ''axis'' of the pencil. The pencil is sometimes referred to as a axial-pencil or fan of planes or a '' sheaf of planes''. For example, the meridians of the globe are defined by the pencil of planes on the axis of Earth's rotation.
Two intersecting planes meet in a line in three-space, and so, determine the axis and hence all of the planes in the pencil.
The four-space of
A pencil of planes, is the set of planes through a given straight line in three-space, called the ''axis'' of the pencil. The pencil is sometimes referred to as a axial-pencil or fan of planes or a '' sheaf of planes''. For example, the meridians of the globe are defined by the pencil of planes on the axis of Earth's rotation.
Two intersecting planes meet in a line in three-space, and so, determine the axis and hence all of the planes in the pencil.
The four-space of
 Any two circles in the plane have a common
Any two circles in the plane have a common
 Another type of pencil of circles can be obtained as follows. Consider a given circle (called the ''generator circle'') and a distinguished point on the generator circle. The set of all circles that pass through and have their centers on the generator circle form a pencil of circles. The
Another type of pencil of circles can be obtained as follows. Consider a given circle (called the ''generator circle'') and a distinguished point on the generator circle. The set of all circles that pass through and have their centers on the generator circle form a pencil of circles. The
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
s that pass through two given points in a plane.
Although the definition of a pencil is rather vague, the common characteristic is that the pencil is completely determined by any two of its members. Analogously, a set of geometric objects that are determined by any three of its members is called a bundle. Thus, the set of all lines through a point in three-space is a bundle of lines, any two of which determine a pencil of lines. To emphasize the two-dimensional nature of such a pencil, it is sometimes referred to as a ''flat pencil''.
Any geometric object can be used in a pencil. The common ones are lines, planes, circles, conics, spheres, and general curves. Even points can be used. A pencil of points is the set of all points on a given line. A more common term for this set is a ''range'' of points.
Pencil of lines
In a plane, let and be two distinct intersecting lines. For concreteness, suppose that has the equation, and has the equation . Then ::, represents, for suitable scalars and , any line passing through the intersection of and . This set of lines passing through a common point is called a pencil of lines. The common point of a pencil of lines is called the '' vertex'' of the pencil. In an affine plane with the reflexive variant of parallelism, a set of parallel lines forms anequivalence class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements ...
called a pencil of parallel lines. This terminology is consistent with the above definition since in the unique projective extension of the affine plane to a projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, paral ...
a single point (point at infinity
In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line.
In the case of an affine plane (including the Euclidean plane), there is one ideal point for each pencil of parallel lines of the plane. Ad ...
) is added to each line in the pencil of parallel lines, thus making it a pencil in the above sense in the projective plane.
A pencil of half-lines, also called a half-pencil, is the set of half-lines sharing a common vertex. It's used in optics as a model for pencil beam
In optics, a pencil or pencil of rays, also known as a pencil beam or narrow beam, is a geometric construct (pencil of half-lines) used to describe a Light beam, beam or portion of a beam of electromagnetic radiation or charged subatomic particl ...
s.
Pencil of planes
 A pencil of planes, is the set of planes through a given straight line in three-space, called the ''axis'' of the pencil. The pencil is sometimes referred to as a axial-pencil or fan of planes or a '' sheaf of planes''. For example, the meridians of the globe are defined by the pencil of planes on the axis of Earth's rotation.
Two intersecting planes meet in a line in three-space, and so, determine the axis and hence all of the planes in the pencil.
The four-space of
A pencil of planes, is the set of planes through a given straight line in three-space, called the ''axis'' of the pencil. The pencil is sometimes referred to as a axial-pencil or fan of planes or a '' sheaf of planes''. For example, the meridians of the globe are defined by the pencil of planes on the axis of Earth's rotation.
Two intersecting planes meet in a line in three-space, and so, determine the axis and hence all of the planes in the pencil.
The four-space of quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s can be seen as an axial pencil of complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
s all sharing the same real line. In fact, quaternions contain a sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
of imaginary unit
The imaginary unit or unit imaginary number () is a mathematical constant that is a solution to the quadratic equation Although there is no real number with this property, can be used to extend the real numbers to what are called complex num ...
s, i.e., . And a pair of antipodal points on this sphere, together with the real axis, generate a complex plane. The union of all these complex planes constitutes the 4-algebra of quaternions.
Pencil of circles
radical axis
In Euclidean geometry, the radical axis of two non-concentric circles is the set of points whose Power of a point, power with respect to the circles are equal. For this reason the radical axis is also called the power line or power bisector of ...
, which is the line consisting of all the points that have the same power with respect to the two circles. A pencil of circles (or coaxial system) is the set of all circles in the plane with the same radical axis. To be inclusive, concentric circles are said to have the line at infinity
In geometry and topology, the line at infinity is a projective line that is added to the affine plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at ...
as a radical axis.
There are five types of pencils of circles, the two families of Apollonian circles in the illustration above represent two of them. Each type is determined by two circles called the ''generators'' of the pencil. When described algebraically, it is possible that the equations may admit imaginary solutions. The types are:
*An ''elliptic pencil'' (red family of circles in the figure) is defined by two generators that pass through each other in exactly ''two'' points. Every circle of an elliptic pencil passes through the same two points. An elliptic pencil does not include any imaginary circles.
*A ''hyperbolic pencil'' (blue family of circles in the figure) is defined by two generators that do not intersect each other at ''any'' point. It includes real circles, imaginary circles, and two degenerate point circles called the ''Poncelet points'' of the pencil. Each point in the plane belongs to exactly one circle of the pencil.
*A ''parabolic pencil'' (as a limiting case) is defined where two generating circles are tangent to each other at a ''single'' point. It consists of a family of real circles, all tangent to each other at a single common point. The degenerate circle with radius zero at that point also belongs to the pencil.
*A family of concentric circles centered at a common center (may be considered a special case of a hyperbolic pencil where the other point is the point at infinity).
*The family of straight lines through a common point; these should be interpreted as circles that all pass through the point at infinity (may be considered a special case of an elliptic pencil).
Properties
A circle that is orthogonal to two fixed circles is orthogonal to every circle in the pencil they determine. The circles orthogonal to two fixed circles form a pencil of circles. Two circles determine two pencils, the unique pencil that contains them and the pencil of circles orthogonal to them. The radical axis of one pencil consists of the centers of the circles of the other pencil. If one pencil is of elliptic type, the other is of hyperbolic type and vice versa. The radical axis of any pencil of circles, interpreted as an infinite-radius circle, belongs to the pencil. Any three circles belong to a common pencil whenever all three pairs share the same radical axis and their centers arecollinear
In geometry, collinearity of a set of Point (geometry), points is the property of their lying on a single Line (geometry), line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, t ...
.
Projective space of circles
There is a natural correspondence between circles in the plane and points in three-dimensionalprojective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally ...
(see below); a line in this space corresponds to a one-dimensional continuous family of circles, hence a pencil of points in this space is a pencil of circles in the plane.
Specifically, the equation of a circle of radius centered at a point ,
:
may be rewritten as
:
where .
In this form, multiplying the quadruple by a scalar produces a different quadruple that represents the same circle; thus, these quadruples may be considered to be homogeneous coordinates
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work , are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. ...
for the space of circles. Straight lines may also be represented with an equation of this type in which and should be thought of as being a degenerate form of a circle. When , we may solve for , and ; the latter formula may give (in which case the circle degenerates to a point) or equal to an imaginary number
An imaginary number is the product of a real number and the imaginary unit , is usually used in engineering contexts where has other meanings (such as electrical current) which is defined by its property . The square (algebra), square of an im ...
(in which case the quadruple is said to represent an ''imaginary circle'').
The set of affine combination
In mathematics, an affine combination of is a linear combination
: \sum_^ = \alpha_ x_ + \alpha_ x_ + \cdots +\alpha_ x_,
such that
:\sum_^ =1.
Here, can be elements ( vectors) of a vector space over a field , and the coefficients \alpha_ ...
s of two circles , , that is, the set of circles represented by the quadruple
:
for some value of the parameter ,
forms a pencil; the two circles being the generators of the pencil.
Cardioid as envelope of a pencil of circles
envelope
An envelope is a common packaging item, usually made of thin, flat material. It is designed to contain a flat object, such as a letter (message), letter or Greeting card, card.
Traditional envelopes are made from sheets of paper cut to one o ...
of this pencil is a cardioid.
Pencil of spheres
A sphere is uniquely determined by four points that are notcoplanar
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. How ...
. More generally, a sphere is uniquely determined by four conditions such as passing through a point, being tangent to a plane, etc. This property is analogous to the property that three non-collinear points determine a unique circle in a plane.
Consequently, a sphere is uniquely determined by (that is, passes through) a circle and a point not in the plane of that circle.
By examining the common solutions of the equations of two spheres, it can be seen that two spheres intersect in a circle and the plane containing that circle is called the radical plane of the intersecting spheres. Although the radical plane is a real plane, the circle may be imaginary (the spheres have no real point in common) or consist of a single point (the spheres are tangent at that point)..
If and are the equations of two distinct spheres then
:
is also the equation of a sphere for arbitrary values of the parameters and . The set of all spheres satisfying this equation is called a pencil of spheres determined by the original two spheres. In this definition a sphere is allowed to be a plane (infinite radius, center at infinity) and if both the original spheres are planes then all the spheres of the pencil are planes, otherwise there is only one plane (the radical plane) in the pencil.
If the pencil of spheres does not consist of all planes, then there are three types of pencils:
* If the spheres intersect in a real circle , then the pencil consists of all the spheres containing , including the radical plane. The centers of all the ordinary spheres in the pencil lie on a line passing through the center of and perpendicular to the radical plane.
* If the spheres intersect in an imaginary circle, all the spheres of the pencil also pass through this imaginary circle but as ordinary spheres they are disjoint (have no real points in common). The line of centers is perpendicular to the radical plane, which is a real plane in the pencil containing the imaginary circle.
* If the spheres intersect in a point , all the spheres in the pencil are tangent at and the radical plane is the common tangent plane of all these spheres. The line of centers is perpendicular to the radical plane at .
All the tangent lines from a fixed point of the radical plane to the spheres of a pencil have the same length.
The radical plane is the locus of the centers of all the spheres that are orthogonal to all the spheres in a pencil. Moreover, a sphere orthogonal to any two spheres of a pencil of spheres is orthogonal to all of them and its center lies in the radical plane of the pencil.
Pencil of conics
A (non-degenerate)conic
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, thou ...
is completely determined by five points in general position (no three collinear) in a plane and the system of conics which pass through a fixed set of four points (again in a plane and no three collinear) is called a pencil of conics. The four common points are called the ''base points'' of the pencil. Through any point other than a base point, there passes a single conic of the pencil. This concept generalizes a pencil of circles.
In a projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, paral ...
defined over an algebraically closed field
In mathematics, a field is algebraically closed if every non-constant polynomial in (the univariate polynomial ring with coefficients in ) has a root in . In other words, a field is algebraically closed if the fundamental theorem of algebra ...
any two conics meet in four points (counted with multiplicity) and so, determine the pencil of conics based on these four points. Furthermore, the four base points determine three line pairs ( degenerate conics through the base points, each line of the pair containing exactly two base points) and so each pencil of conics will contain at most three degenerate conics.
A pencil of conics can be represented algebraically in the following way. Let and be two distinct conics in a projective plane defined over an algebraically closed field . For every pair of elements of , not both zero, the expression:
::
represents a conic in the pencil determined by and . This symbolic representation can be made concrete with a slight abuse of notation (using the same notation to denote the object as well as the equation defining the object.) Thinking of , say, as a ternary quadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two (" form" is another name for a homogeneous polynomial). For example,
4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong t ...
, then is the equation of the "conic ". Another concrete realization would be obtained by thinking of as the 3×3 symmetric matrix which represents it. If and have such concrete realizations then every member of the above pencil will as well. Since the setting uses homogeneous coordinates in a projective plane, two concrete representations (either equations or matrices) give the same conic if they differ by a non-zero multiplicative constant.
Pencil of plane curves
More generally, a pencil is the special case of alinear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family.
These arose first in the f ...
in which the parameter space is a projective line
In projective geometry and mathematics more generally, a projective line is, roughly speaking, the extension of a usual line by a point called a '' point at infinity''. The statement and the proof of many theorems of geometry are simplified by the ...
. Typical pencils of curves in the projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane (geometry), plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines (namely, paral ...
, for example, are written as
:
where , are plane curves.
History
Desargues is credited with inventing the term "pencil of lines" (''ordonnance de lignes''). An early author of modern projective geometry G. B. Halsted introduced the terms ''copunctal'' and ''flat-pencil'' to defineangle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
: "Straights with the same cross are copunctal." Also "The aggregate of all coplanar, copunctal straights is called a ''flat-pencil''" and "A piece of a flat-pencil bounded by two of the straights as ''sides'', is called an ''angle''."
See also
*Bundle adjustment
In photogrammetry and computer stereo vision, bundle adjustment is simultaneous refining of the 3D coordinates describing the scene geometry, the parameters of the relative motion, and the optical characteristics of the camera(s) employed to acq ...
* Lefschetz pencil
* Matrix pencil
* Pencil beam
In optics, a pencil or pencil of rays, also known as a pencil beam or narrow beam, is a geometric construct (pencil of half-lines) used to describe a Light beam, beam or portion of a beam of electromagnetic radiation or charged subatomic particl ...
* Fibration
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics.
Fibrations are used, for example, in Postnikov systems or obstruction theory.
In this article, all ma ...
* Locus
Notes
References
* * * * * * * * * . * *External links
*{{MathWorld, title=Pencil, urlname=Pencil, mode=cs2 Algebraic geometry Projective geometry