mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...

and its applications, a parametric family or a parameterized family is a

family Family (from ) is a Social group, group of people related either by consanguinity (by recognized birth) or Affinity (law), affinity (by marriage or other relationship). It forms the basis for social order. Ideally, families offer predictabili ...

of objects (a set of related objects) whose differences depend only on the chosen values for a set of

parameter A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...

s. Common examples are parametrized (families of) functions, probability distributions, curves, shapes, etc.

In probability and its applications

Probability distribution functions for normal distribution

For example, the probability density function of a random variable may depend on a parameter . In that case, the function may be denoted

f_X( \cdot \, ; \theta)

to indicate the dependence on the parameter . is not a formal argument of the function as it is considered to be fixed. However, each different value of the parameter gives a different probability density function. Then the ''parametric family'' of densities is the set of functions

\

, where denotes the

parameter space The parameter space is the space of all possible parameter values that define a particular mathematical model. It is also sometimes called weight space, and is often a subset of finite-dimensional Euclidean space. In statistics, parameter spaces a ...

, the set of all possible values that the parameter can take. As an example, the

normal distribution In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac ...

is a family of similarly-shaped distributions parametrized by their

mean A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...

and their

variance In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...

. In

decision theory Decision theory or the theory of rational choice is a branch of probability theory, probability, economics, and analytic philosophy that uses expected utility and probabilities, probability to model how individuals would behave Rationality, ratio ...

, two-moment decision models can be applied when the decision-maker is faced with random variables drawn from a location-scale family of probability distributions.

In algebra and its applications

economics Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services. Economics focuses on the behaviour and interac ...

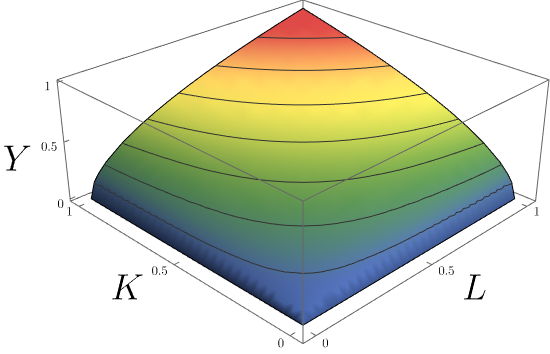
, the

Cobb–Douglas production function In economics and econometrics, the Cobb–Douglas production function is a particular functional form of the production function, widely used to represent the technological relationship between the amounts of two or more inputs (particularly phy ...

is a family of

production function In economics, a production function gives the technological relation between quantities of physical inputs and quantities of output of goods. The production function is one of the key concepts of mainstream economics, mainstream neoclassical econ ...

s parametrized by the elasticities of output with respect to the various

factors of production In economics, factors of production, resources, or inputs are what is used in the production process to produce output—that is, goods and services. The utilised amounts of the various inputs determine the quantity of output according to the rela ...

algebra Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...

, the

quadratic equation In mathematics, a quadratic equation () is an equation that can be rearranged in standard form as ax^2 + bx + c = 0\,, where the variable (mathematics), variable represents an unknown number, and , , and represent known numbers, where . (If and ...

, for example, is actually a family of equations parametrized by the

coefficient In mathematics, a coefficient is a Factor (arithmetic), multiplicative factor involved in some Summand, term of a polynomial, a series (mathematics), series, or any other type of expression (mathematics), expression. It may be a Dimensionless qu ...

s of the variable and of its square and by the

constant term In mathematics, a constant term (sometimes referred to as a free term) is a term in an algebraic expression that does not contain any variables and therefore is constant. For example, in the quadratic polynomial, :x^2 + 2x + 3,\ The number 3 i ...

References

{{reflist Mathematical terminology Theory of probability distributions

In probability and its applications

In algebra and its applications

See also

References