Open universe

In physical cosmology, the shape of the universe refers to both its local and global geometry. Local geometry is defined primarily by its curvature, while the global geometry is characterised by its topology (which itself is constrained by curvature). General relativity explains how spatial curvature (local geometry) is constrained by gravity. The global topology of the universe cannot be deduced from measurements of curvature inferred from observations within the family of homogeneous general relativistic models alone, due to the existence of locally indistinguishable spaces with varying global topological characteristics. For example; a multiply connected space like a 3 torus has everywhere zero curvature but is finite in extent, whereas a flat simply connected space is infinite in extent (such as Euclidean space).

Current observational evidence ( WMAP, BOOMERanG, and Planck for example) imply that the observable universe is spatially flat to within a 0.4% margin of error of the curvature density parameter with an unknown global topology. It is currently unknown whether the universe is simply connected like euclidean space or multiply connected like a torus. To date, compelling evidence has been found suggesting the topology of the universe is simply connected, though multiplied connections can also be possible by astronomical observations.

Shape of the observable universe

The universe's structure can be examined from two angles:
# Local geometry: This relates to the curvature of the universe, primarily concerning what we can observe.
# Global geometry: This pertains to the universe's overall shape and structure.
The observable universe (of a given current observer) is a roughly spherical region extending about 46 billion light-years in every direction (from that observer, the observer being the current Earth, unless specified otherwise). It appears older and more redshifted the deeper we look into space. In theory, we could look all the way back to the Big Bang, but in practice, we can only see up to the cosmic microwave background (CMB) (roughly years after the Big Bang) as anything beyond that is opaque. Studies show that the observable universe is isotropic and homogeneous on the largest scales.

If the observable universe encompasses the entire universe, we might determine its structure through observation. However, if the observable universe is smaller, we can only grasp a portion of it, making it impossible to deduce the global geometry through observation. Different mathematical models of the universe's global geometry can be constructed, all consistent with current observations and general relativity. Hence, it is unclear whether the observable universe matches the entire universe or is significantly smaller, though it is generally accepted that the universe is larger than the observable universe.

The universe may be compact in some dimensions and not in others, similar to how a cuboid is longer in one dimension than the others. Scientists test these models by looking for novel implications – phenomena not yet observed but necessary if the model is accurate. For instance, a small closed universe would produce multiple images of the same object in the sky, though not necessarily of the same age. As of 2024, current observational evidence suggests that the observable universe is spatially flat with an unknown global structure.

Curvature of the universe

The curvature is a quantity describing how the geometry of a space differs locally from flat space. The curvature of any locally isotropic space (and hence of a locally isotropic universe) falls into one of the three following cases:
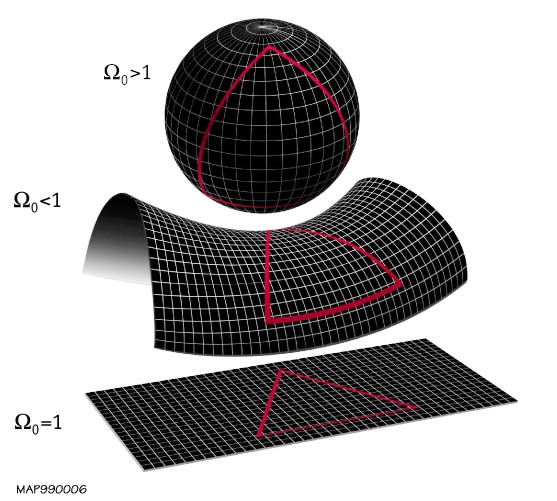
# Zero curvature (flat)a drawn triangle's angles add up to 180° and the Pythagorean theorem holds; such 3-dimensional space is locally modeled by Euclidean space .
# Positive curvaturea drawn triangle's angles add up to more than 180°; such 3-dimensional space is locally modeled by a region of a 3-sphere .
# Negative curvaturea drawn triangle's angles add up to less than 180°; such 3-dimensional space is locally modeled by a region of a hyperbolic space .

Curved geometries are in the domain of non-Euclidean geometry. An example of a positively curved space would be the surface of a sphere such as the Earth. A triangle drawn from the equator to a pole will have at least two angles equal 90°, which makes the sum of the 3 angles greater than 180°. An example of a negatively curved surface would be the shape of a saddle or mountain pass. A triangle drawn on a saddle surface will have the sum of the angles adding up to less than 180°.

General relativity explains that mass and energy bend the curvature of spacetime and is used to determine what curvature the universe has by using a value called the density parameter, represented with Omega (). The density parameter is the average density of the universe divided by the critical energy density, that is, the mass energy needed for a universe to be flat. Put another way,
* If , the universe is flat.
* If , there is positive curvature.
* If , there is negative curvature.

Scientists could experimentally calculate to determine the curvature two ways. One is to count all the mass–energy in the universe and take its average density, then divide that average by the critical energy density. Data from the Wilkinson Microwave Anisotropy Probe (WMAP) as well as the Planck spacecraft give values for the three constituents of all the mass–energy in the universe – normal mass (baryonic matter and dark matter), relativistic particles (predominantly photons and neutrinos), and dark energy or the cosmological constant:
: Ω_mass ≈
: Ω_relativistic ≈
: Ω_Λ ≈
: Ω_total = Ω_mass + Ω_relativistic + Ω_Λ =
The actual value for critical density value is measured as ''ρ''_critical = . From these values, within experimental error, the universe seems to be spatially flat.

Another way to measure Ω is to do so geometrically by measuring an angle across the observable universe. This can be done by using the CMB and measuring the power spectrum and temperature anisotropy. For instance, one can imagine finding a gas cloud that is not in thermal equilibrium due to being so large that light speed cannot propagate the thermal information. Knowing this propagation speed, we then know the size of the gas cloud as well as the distance to the gas cloud, we then have two sides of a triangle and can then determine the angles. Using a method similar to this, the BOOMERanG experiment has determined that the sum of the angles to 180° within experimental error, corresponding to .

These and other astronomical measurements constrain the spatial curvature to be very close to zero, although they do not constrain its sign. This means that although the local geometries of spacetime are generated by the theory of relativity based on spacetime intervals, we can approximate ''3-space'' by the familiar Euclidean geometry.

The Friedmann–Lemaître–Robertson–Walker (FLRW) model using Friedmann equations is commonly used to model the universe. The FLRW model provides a curvature of the universe based on the mathematics of fluid dynamics, that is, modeling the matter within the universe as a perfect fluid. Although stars and structures of mass can be introduced into an "almost FLRW" model, a strictly FLRW model is used to approximate the local geometry of the observable universe. Another way of saying this is that, if all forms of dark energy are ignored, then the curvature of the universe can be determined by measuring the average density of matter within it, assuming that all matter is evenly distributed (rather than the distortions caused by 'dense' objects such as galaxies). This assumption is justified by the observations that, while the universe is "weakly" inhomogeneous and anisotropic (see the large-scale structure of the cosmos), it is on average homogeneous and isotropic when analyzed at a sufficiently large spatial scale.

Global universal structure

Global structure covers the geometry and the topology of the whole universe—both the observable universe and beyond. While the local geometry does not determine the global geometry completely, it does limit the possibilities, particularly a geometry of a constant curvature. The universe is often taken to be a geodesic manifold, free of topological defects; relaxing either of these complicates the analysis considerably. A global geometry is a local geometry plus a topology. It follows that a topology alone does not give a global geometry: for instance, Euclidean 3-space and hyperbolic 3-space have the same topology but different global geometries.

As stated in the introduction, investigations within the study of the global structure of the universe include:
* whether the universe is infinite or finite in extent,
* whether the geometry of the global universe is flat, positively curved, or negatively curved, and,
* whether the topology is simply connected (for example, like a sphere) or else multiply connected (for example, like a torus).

Infinite or finite

One of the unanswered questions about the universe is whether it is infinite or finite in extent. For intuition, it can be understood that a finite universe has a finite volume that, for example, could be in theory filled with a finite amount of material, while an infinite universe is unbounded and no numerical volume could possibly fill it. Mathematically, the question of whether the universe is infinite or finite is referred to as boundedness. An infinite universe (unbounded metric space) means that there are points arbitrarily far apart: for any distance , there are points that are of a distance at least apart. A finite universe is a bounded metric space, where there is some distance such that all points are within distance of each other. The smallest such is called the diameter of the universe, in which case the universe has a well-defined "volume" or "scale".

With or without boundary

Assuming a finite universe, the universe can either have an edge or no edge. Many finite mathematical spaces, e.g., a disc, have an edge or boundary. Spaces that have an edge are difficult to treat, both conceptually and mathematically. Namely, it is difficult to state what would happen at the edge of such a universe. For this reason, spaces that have an edge are typically excluded from consideration.

However, there exist many finite spaces, such as the 3-sphere and 3-torus, that have no edges. Mathematically, these spaces are referred to as being compact without boundary. The term compact means that it is finite in extent ("bounded") and complete. The term "without boundary" means that the space has no edges. Moreover, so that calculus can be applied, the universe is typically assumed to be a differentiable manifold. A mathematical object that possesses all these properties, compact without boundary and differentiable, is termed a closed manifold. The 3-sphere and 3-torus are both closed manifolds.

Observational methods

In the 1990s and early 2000s, empirical methods for determining the global topology using measurements on scales that would show multiple imaging were proposed and applied to cosmological observations.

In the 2000s and 2010s, it was shown that, since the universe is inhomogeneous as shown in the cosmic web of large-scale structure, acceleration effects measured on local scales in the patterns of the movements of galaxies should, in principle, reveal the global topology of the universe.

Curvature

The curvature of the universe places constraints on the topology. If the spatial geometry is spherical, i.e., possess positive curvature, the topology is compact. For a flat (zero curvature) or a hyperbolic (negative curvature) spatial geometry, the topology can be either compact or infinite. Many textbooks erroneously state that a flat or hyperbolic universe implies an infinite universe; however, the correct statement is that a flat universe that is also simply connected implies an infinite universe. For example, Euclidean space is flat, simply connected, and infinite, but there are tori that are flat, multiply connected, finite, and compact (see flat torus).

In general, local to global theorems in Riemannian geometry relate the local geometry to the global geometry. If the local geometry has constant curvature, the global geometry is very constrained, as described in Thurston geometries.

The latest research shows that even the most powerful future experiments (like the SKA) will not be able to distinguish between a flat, open and closed universe if the true value of cosmological curvature parameter is smaller than 10⁻⁴. If the true value of the cosmological curvature parameter is larger than 10⁻³ we will be able to distinguish between these three models even now.

Final results of the ''Planck'' mission, released in 2018, show the cosmological curvature parameter, , to be , consistent with a flat universe. (i.e. positive curvature: , , , negative curvature: , , , zero curvature: , , ).

Universe with zero curvature

In a universe with zero curvature, the local geometry is flat. The most familiar such global structure is that of Euclidean space, which is infinite in extent. Flat universes that are finite in extent include the torus and Klein bottle. Moreover, in three dimensions, there are 10 finite closed flat 3-manifolds, of which 6 are orientable and 4 are non-orientable. These are the Bieberbach manifolds. The most familiar is the aforementioned 3-torus universe.

In the absence of dark energy, a flat universe expands forever but at a continually decelerating rate, with expansion asymptotically approaching zero. With dark energy, the expansion rate of the universe initially slows down, due to the effect of gravity, but eventually increases. The ultimate fate of the universe is the same as that of an open universe in the sense that space will continue expanding forever.

A flat universe can have zero total energy.

Universe with positive curvature

A positively curved universe is described by elliptic geometry, and can be thought of as a three-dimensional hypersphere, or some other spherical 3-manifold (such as the Poincaré dodecahedral space), all of which are quotients of the 3-sphere.

Poincaré dodecahedral space is a positively curved space, colloquially described as "soccerball-shaped", as it is the quotient of the 3-sphere by the binary icosahedral group, which is very close to icosahedral symmetry, the symmetry of a soccer ball. This was proposed by Jean-Pierre Luminet and colleagues in 2003 and an optimal orientation on the sky for the model was estimated in 2008.

Universe with negative curvature

A hyperbolic universe, one of a negative spatial curvature, is described by hyperbolic geometry, and can be thought of locally as a three-dimensional analog of an infinitely extended saddle shape. There are a great variety of hyperbolic 3-manifolds, and their classification is not completely understood. Those of finite volume can be understood via the Mostow rigidity theorem. For hyperbolic local geometry, many of the possible three-dimensional spaces are informally called "horn topologies", so called because of the shape of the pseudosphere, a canonical model of hyperbolic geometry. An example is the Picard horn, a negatively curved space, colloquially described as "funnel-shaped".

Curvature: open or closed

When cosmologists speak of the universe as being "open" or "closed", they most commonly are referring to whether the curvature is negative or positive, respectively. These meanings of open and closed are different from the mathematical meaning of open and closed used for sets in topological spaces and for the mathematical meaning of open and closed manifolds, which gives rise to ambiguity and confusion. In mathematics, there are definitions for a closed manifold (i.e., compact without boundary) and open manifold (i.e., one that is not compact and without boundary). A "closed universe" is necessarily a closed manifold. An "open universe" can be either a closed or open manifold. For example, in the Friedmann–Lemaître–Robertson–Walker (FLRW) model, the universe is considered to be without boundaries, in which case "compact universe" could describe a universe that is a closed manifold.

See also

*
* —A string-theory-related model depicting a five-dimensional, membrane-shaped universe; an alternative to the Hot Big Bang Model, whereby the universe is described to have originated when two membranes collided at the fifth dimension
* for 6 or 7 extra space-like dimensions all with a ''compact'' topology
*
*
*
*
* —The "remarkable theorem" discovered by Gauss, which showed there is an intrinsic notion of curvature for surfaces. This is used by Riemann to generalize the (intrinsic) notion of curvature to higher-dimensional spaces
*
*

References

External links

Geometry of the Universe
at icosmos.co.uk
*
*
*
* Possible wrap-around dodecahedral shape of the universe
* Classification o

in the Lambda-CDM model.
*
*

What do you mean the universe is flat?
Scientific American Blog explanation of a flat universe and the curved spacetime in the universe.

{{Portal bar, Astronomy, Stars, Outer space, Physics

Differential geometry
General relativity
Physical cosmological concepts
Unsolved problems in astronomy
Big Bang