Omnitruncated 4-simplex on:
[Wikipedia]
[Google]
[Amazon]
In four-dimensional

 The runcitruncated
The runcitruncated

20 (4.4.6) , - , bgcolor=#e7dcc3, Faces , 150 , 90{4}
60{6} , - , bgcolor=#e7dcc3, Edges , colspan=2, 240 , - , bgcolor=#e7dcc3, Vertices , colspan=2, 120 , - , bgcolor=#e7dcc3,
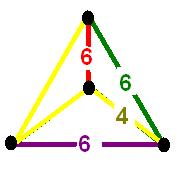

Omnitruncated 5-cell ,
Dual to omnitruncated 5-cell
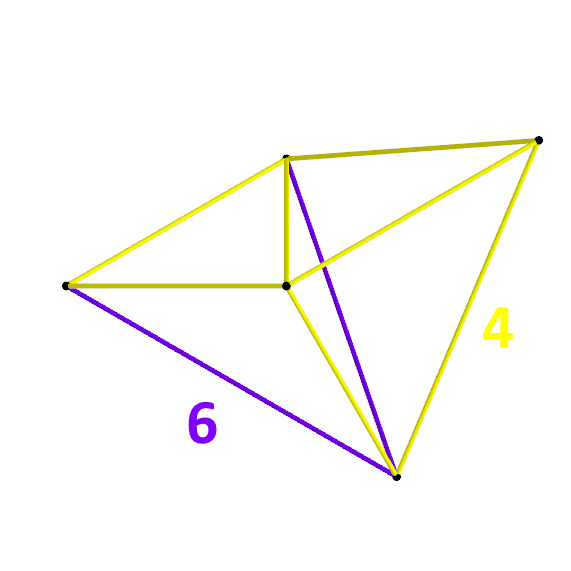
Perspective
Centered on



 The full snub 5-cell or omnisnub 5-cell, defined as an Alternation (geometry), alternation of the omnitruncated 5-cell, cannot be made uniform, but it can be given Coxeter diagram , and
The full snub 5-cell or omnisnub 5-cell, defined as an Alternation (geometry), alternation of the omnitruncated 5-cell, cannot be made uniform, but it can be given Coxeter diagram , and
wiley.com
*** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380–407, MR 2,10*** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559–591*** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3–45* Norman Johnson ''Uniform Polytopes'', Manuscript (1991) ** N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. * * o3x3x3o - spid, x3x3o3x - prip, x3x3x3x - gippid {{Polytopes Uniform 4-polytopes
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a runcinated 5-cell is a convex uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedron, uniform polyhedra, and faces are regular polygons.
There are 47 non-Prism (geometry), prism ...
, being a runcination
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers.
It is a higher order truncatio ...
(a 3rd order truncation, up to face-planing) of the regular 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional space, four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pe ...
.
There are 3 unique degrees of runcinations of the 5-cell, including with permutations, truncations, and cantellations.
Runcinated 5-cell
The runcinated 5-cell or small prismatodecachoron is constructed by expanding thecells
Cell most often refers to:
* Cell (biology), the functional basic unit of life
* Cellphone, a phone connected to a cellular network
* Clandestine cell, a penetration-resistant form of a secret or outlawed organization
* Electrochemical cell, a d ...
of a 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional space, four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pe ...
radially and filling in the gaps with triangular prism
PRISM is a code name for a program under which the United States National Security Agency (NSA) collects internet communications from various U.S. internet companies. The program is also known by the SIGAD . PRISM collects stored internet ...
s (which are the face prisms and edge figures) and tetrahedra
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
(cells of the dual 5-cell). It consists of 10 tetrahedra and 20 triangular prisms. The 10 tetrahedra correspond with the cells of a 5-cell and its dual.
Topologically, under its highest symmetry, 3,3,3
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pentahedroid, tetrahedral ...
E. L. Elte
Emanuel Lodewijk Elte (16 March 1881 in Amsterdam – 9 April 1943 in Sobibór) Emanuël Lodewijk Elte
...
identified it in 1912 as a semiregular polytope.
...
Alternative names
* Runcinated5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional space, four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pe ...
( Norman Johnson)
* Runcinated pentachoron
* Runcinated 4-simplex
* Expanded 5-cell/4-simplex/pentachoron
* Small prismatodecachoron (Acronym: Spid) (Jonathan Bowers)
Structure
Two of the ten tetrahedral cells meet at each vertex. The triangular prisms lie between them, joined to them by their triangular faces and to each other by their square faces. Each triangular prism is joined to its neighbouring triangular prisms in ''anti'' orientation (i.e., if edges A and B in the shared square face are joined to the triangular faces of one prism, then it is the other two edges that are joined to the triangular faces of the other prism); thus each pair of adjacent prisms, if rotated into the samehyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
, would form a gyrobifastigium
In geometry, the gyrobifastigium is a polyhedron that is constructed by attaching a triangular prism to square face of another one. It is an example of a Johnson solid. It is the only Johnson solid that can tile three-dimensional space.
Const ...
.Configuration
Seen in a configuration matrix, all incidence counts between elements are shown. The diagonalf-vector
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.
Research in polyhedral com ...
numbers are derived through the Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.
Construction process ...
, dividing the full group order of a subgroup order by removing one mirror at a time.
Dissection
The ''runcinated 5-cell'' can be dissected by a centralcuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
into two tetrahedral cupola. This dissection is analogous to the 3D cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
being dissected by a central hexagon into two triangular cupola
In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. The triangular cupola can b ...
.
: 
Images
Coordinates
TheCartesian coordinate
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
s of the vertices of an origin-centered runcinated 5-cell with edge length 2 are:
An alternate simpler set of coordinates can be made in 5-space, as 20 permutations of:
: (0,1,1,1,2)
This construction exists as one of 32 orthant
In geometry, an orthant or hyperoctant is the analogue in ''n''-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions.
In general an orthant in ''n''-dimensions can be considered the intersection of ''n'' mutu ...
facets of the runcinated 5-orthoplex
In Five-dimensional space, five-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order Truncation (geometry), truncation (runcination) of the regular 5-orthoplex.
There are 8 runcinations of the 5-orthoplex wi ...
.
A second construction in 5-space, from the center of a rectified 5-orthoplex
In five-dimensional geometry, a rectified 5-orthoplex is a convex uniform 5-polytope, being a Rectification (geometry), rectification of the regular 5-orthoplex.
There are 5 degrees of rectifications for any 5-polytope, the zeroth here being the ...
is given by coordinate permutations of:
: (1,-1,0,0,0)
Root vectors
Its 20 vertices represent the root vectors of thesimple Lie group
In mathematics, a simple Lie group is a connected non-abelian Lie group ''G'' which does not have nontrivial connected normal subgroups. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symm ...
A4. It is also the vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
for the 5-cell honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb (geometry), honeycomb. It is composed of 5-cells and recti ...
in 4-space.
Cross-sections
The maximal cross-section of the runcinated 5-cell with a 3-dimensionalhyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
is a cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
. This cross-section divides the runcinated 5-cell into two tetrahedral hypercupolae consisting of 5 tetrahedra and 10 triangular prisms each.
Projections
The tetrahedron-firstorthographic projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Plane (mathematics), two dimensions. Orthographic projection is a form of parallel projection in ...
of the runcinated 5-cell into 3-dimensional space has a cuboctahedral envelope. The structure of this projection is as follows:
* The cuboctahedral envelope is divided internally as follows:
:* Four flattened tetrahedra join 4 of the triangular faces of the cuboctahedron to a central tetrahedron. These are the images of 5 of the tetrahedral cells.
:* The 6 square faces of the cuboctahedron are joined to the edges of the central tetrahedron via distorted triangular prisms. These are the images of 6 of the triangular prism cells.
:* The other 4 triangular faces are joined to the central tetrahedron via 4 triangular prisms (distorted by projection). These are the images of another 4 of the triangular prism cells.
:* This accounts for half of the runcinated 5-cell (5 tetrahedra and 10 triangular prisms), which may be thought of as the 'northern hemisphere'.
* The other half, the 'southern hemisphere', corresponds to an isomorphic division of the cuboctahedron in dual orientation, in which the central tetrahedron is dual to the one in the first half. The triangular faces of the cuboctahedron join the triangular prisms in one hemisphere to the flattened tetrahedra in the other hemisphere, and vice versa. Thus, the southern hemisphere contains another 5 tetrahedra and another 10 triangular prisms, making the total of 10 tetrahedra and 20 triangular prisms.
Related skew polyhedron
Theregular skew polyhedron
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedra which include the possibility of nonplanar faces or vertex figures. Coxeter looked at skew vertex figures which created new 4-dimensional regular polyhedr ...
, , exists in 4-space with 6 squares around each vertex, in a zig-zagging nonplanar vertex figure. These square faces can be seen on the runcinated 5-cell, using all 60 edges and 20 vertices. The 40 triangular faces of the runcinated 5-cell can be seen as removed. The dual regular skew polyhedron, , is similarly related to the hexagonal faces of the bitruncated 5-cell
In geometry, a truncated 5-cell is a uniform 4-polytope (4-dimensional uniform polytope) formed as the truncation of the regular 5-cell.
There are two degrees of truncations, including a bitruncation.
Truncated 5-cell
The truncated 5-cell, tru ...
.
Runcitruncated 5-cell
 The runcitruncated
The runcitruncated 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional space, four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pe ...
or prismatorhombated pentachoron is composed of 60 vertices, 150 edges, 120 faces, and 30 cells. The cells are: 5 truncated tetrahedra
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncating all 4 vertices of a regular tetrahedron. ...
, 10 hexagonal prism
In geometry, the hexagonal prism is a Prism (geometry), prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 face (geometry), faces, 18 Edge (geometry), edges, and 12 vertex (geometry), vertices..
As a semiregular polyhedro ...
s, 10 triangular prism
In geometry, a triangular prism or trigonal prism is a Prism (geometry), prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a ''right triangular prism''. A right triangul ...
s, and 5 cuboctahedra. Each vertex is surrounded by five cells: one truncated tetrahedron, two hexagonal prisms, one triangular prism, and one cuboctahedron; the vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
is a rectangular pyramid.
Alternative names
* Runcitruncated pentachoron * Runcitruncated 4-simplex * Diprismatodispentachoron * Prismatorhombated pentachoron (Acronym: prip) (Jonathan Bowers)Configuration
Seen in a configuration matrix, all incidence counts between elements are shown. The diagonalf-vector
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.
Research in polyhedral com ...
numbers are derived through the Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.
Construction process ...
, dividing the full group order of a subgroup order by removing one mirror at a time.
Images
Coordinates
TheCartesian coordinate
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
s of an origin-centered runcitruncated 5-cell having edge length 2 are:
{, class="wikitable mw-collapsible mw-collapsed"
! colspan=2, Coordinates
, -
,
:
:
:
:
:
:
:
:
:
,
:
:
:
:
:
:
:
:
:
,
:
:
:
:
:
:
:
:
:
The vertices can be more simply constructed on a hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
in 5-space, as the permutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
s of:
: (0,1,1,2,3)
This construction is from the positive orthant
In geometry, an orthant or hyperoctant is the analogue in ''n''-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions.
In general an orthant in ''n''-dimensions can be considered the intersection of ''n'' mutu ...
facet
Facets () are flat faces on geometric shapes. The organization of naturally occurring facets was key to early developments in crystallography, since they reflect the underlying symmetry of the crystal structure. Gemstones commonly have facets cu ...
of the runcitruncated 5-orthoplex
In Five-dimensional space, five-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order Truncation (geometry), truncation (runcination) of the regular 5-orthoplex.
There are 8 runcinations of the 5-orthoplex wi ...
.
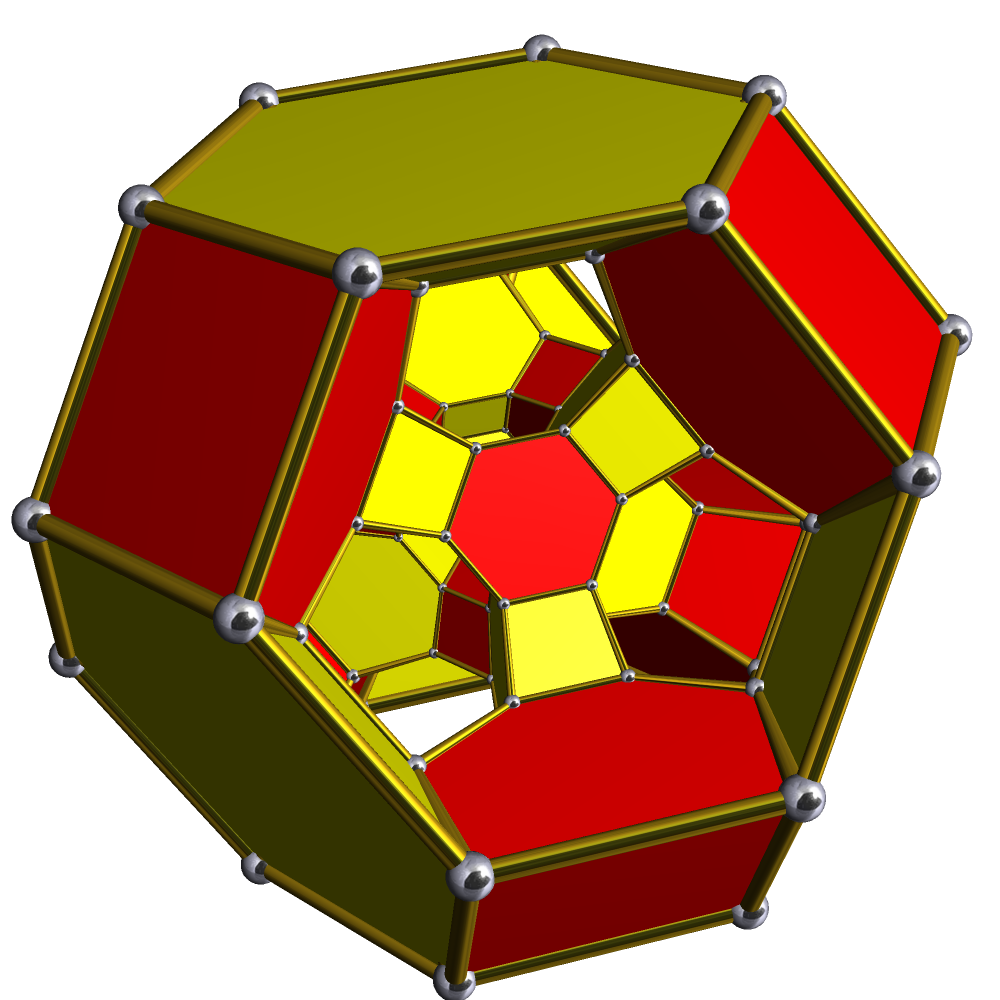
Omnitruncated 5-cell
{, class="wikitable" style="float:right; margin-left:8px; width:250px" , - , bgcolor=#e7dcc3 align=center colspan=3, Omnitruncated 5-cell , - , bgcolor=#ffffff align=center colspan=3,
Schlegel diagram
In geometry, a Schlegel diagram is a projection of a polytope from \mathbb^d into \mathbb^ through a point just outside one of its facets. The resulting entity is a polytopal subdivision of the facet in \mathbb^ that, together with the ori ...
with half of the truncated octahedral cells shown.
, -
, bgcolor=#e7dcc3, Type
, colspan=2, Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedron, uniform polyhedra, and faces are regular polygons.
There are 47 non-Prism (geometry), prism ...
, -
, bgcolor=#e7dcc3, Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
, colspan=2, t0,1,2,3{3,3,3}
, -
, bgcolor=#e7dcc3, Coxeter diagram
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
, colspan=2,
, -
, bgcolor=#e7dcc3, Cells
, 30
, 10 (4.6.6)20 (4.4.6) , - , bgcolor=#e7dcc3, Faces , 150 , 90{4}
60{6} , - , bgcolor=#e7dcc3, Edges , colspan=2, 240 , - , bgcolor=#e7dcc3, Vertices , colspan=2, 120 , - , bgcolor=#e7dcc3,
Vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
, colspan=2, 

Phyllic disphenoid
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex ...
, -
, bgcolor=#e7dcc3, Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...
, colspan=2, Aut
AUT may refer to the following.
Locations
*Austria (ISO 3166-1 country code)
*Agongointo-Zoungoudo Underground Town, Benin
* Aktio–Preveza Undersea Tunnel, Greece
*Airstrip on Atauro Island, East Timor (IATA airport code)
Organizations
*Arri ...
(A4), , order 240
, -
, bgcolor=#e7dcc3, Properties
, colspan=2, convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
, isogonal, zonotope
In geometry, a zonohedron is a convex polyhedron that is point symmetry, centrally symmetric, every face of which is a polygon that is centrally symmetric (a zonogon). Any zonohedron may equivalently be described as the Minkowski addition, Minkows ...
, -
, bgcolor=#e7dcc3, Uniform index
, colspan=2, '' 8'' 9 '' 10''
The omnitruncated 5-cell or great prismatodecachoron is composed of 120 vertices, 240 edges, 150 faces (90 squares
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
and 60 hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is de ...
s), and 30 cells. The cells are: 10 truncated octahedra
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 ...
, and 20 hexagonal prism
In geometry, the hexagonal prism is a Prism (geometry), prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 face (geometry), faces, 18 Edge (geometry), edges, and 12 vertex (geometry), vertices..
As a semiregular polyhedro ...
s. Each vertex is surrounded by four cells: two truncated octahedra, and two hexagonal prisms, arranged in two phyllic disphenoidal vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
s.
Coxeter
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
calls this Hinton's polytope after C. H. Hinton, who described it in his book ''The Fourth Dimension'' in 1906. It forms a uniform honeycomb
In geometry, a uniform honeycomb or uniform tessellation or infinite uniform polytope
In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform Facet (mathematics), facets. Here, "vertex-tra ...
which Coxeter calls Hinton's honeycomb.''The Beauty of Geometry: Twelve Essays'' (1999), Dover Publications, , (The classification of Zonohededra, page 73)
Alternative names
* Omnitruncated5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional space, four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pe ...
* Omnitruncated pentachoron
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pentahedroid, tetrahedral ...
* Omnitruncated 4-simplex
* Great prismatodecachoron (Acronym: gippid) (Jonathan Bowers)
* Hinton's polytope (Coxeter
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
)
Configuration
Seen in a configuration matrix, all incidence counts between elements are shown. The diagonalf-vector
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.
Research in polyhedral com ...
numbers are derived through the Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.
Construction process ...
, dividing the full group order of a subgroup order by removing one mirror at a time.
{, class=wikitable
, -
!, , f''k''
!, f0
! colspan=4, f1
! colspan=6, f2
! colspan=4, f3
, - align=right
, align=left bgcolor=#ffffe0 ,
, rowspan=1, f0
, bgcolor=#e0ffe0, 120
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, - align=right
, align=left bgcolor=#ffffe0 ,
, rowspan=4, f1
, bgcolor=#e0e0e0, 2
, bgcolor=#e0ffe0, 60
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 0
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#e0e0e0, 2
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 60
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 0
, bgcolor=#ffffff, 1
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#e0e0e0, 2
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 60
, bgcolor=#ffffff, *
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 0
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#e0e0e0, 2
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 60
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#ffffff, 0
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, bgcolor=#ffffff, 1
, - align=right
, align=left bgcolor=#ffffe0 ,
, rowspan=6, f2
, bgcolor=#ffffff, 6
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0ffe0, 20
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#ffffff, 4
, bgcolor=#e0e0e0, 2
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 2
, bgcolor=#e0e0e0, 0
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 30
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#ffffff, 4
, bgcolor=#e0e0e0, 2
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 2
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 30
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#ffffff, 6
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 0
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 20
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#ffffff, 4
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 2
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 2
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 30
, bgcolor=#ffffff, *
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#ffffff, 6
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 3
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 20
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 1
, bgcolor=#e0e0e0, 1
, - align=right
, align=left bgcolor=#ffffe0 ,
, rowspan=4, f3
, bgcolor=#e0e0e0, 24
, bgcolor=#ffffff, 12
, bgcolor=#ffffff, 12
, bgcolor=#ffffff, 12
, bgcolor=#ffffff, 0
, bgcolor=#e0e0e0, 4
, bgcolor=#e0e0e0, 6
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 4
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0ffe0, 5
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#e0e0e0, 12
, bgcolor=#ffffff, 6
, bgcolor=#ffffff, 6
, bgcolor=#ffffff, 0
, bgcolor=#ffffff, 6
, bgcolor=#e0e0e0, 2
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 0
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 10
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#e0e0e0, 12
, bgcolor=#ffffff, 6
, bgcolor=#ffffff, 0
, bgcolor=#ffffff, 6
, bgcolor=#ffffff, 6
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 3
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 2
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 10
, bgcolor=#ffffff, *
, - align=right
, align=left bgcolor=#ffffe0 ,
, bgcolor=#e0e0e0, 24
, bgcolor=#ffffff, 0
, bgcolor=#ffffff, 12
, bgcolor=#ffffff, 12
, bgcolor=#ffffff, 12
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 0
, bgcolor=#e0e0e0, 4
, bgcolor=#e0e0e0, 6
, bgcolor=#e0e0e0, 4
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#ffffff, *
, bgcolor=#e0ffe0, 5
Images
{, class=wikitable , +Net
NET may refer to:
Broadcast media
United States
* National Educational Television, the predecessor of the Public Broadcasting Service (PBS) in the United States
* National Empowerment Television, a politically conservative cable TV network ...
, 
Omnitruncated 5-cell ,

Dual to omnitruncated 5-cell
Perspective projections
{, class=wikitable width=600 , + , - align=center ,
Perspective
Schlegel diagram
In geometry, a Schlegel diagram is a projection of a polytope from \mathbb^d into \mathbb^ through a point just outside one of its facets. The resulting entity is a polytopal subdivision of the facet in \mathbb^ that, together with the ori ...
Centered on
truncated octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
, 
Stereographic projection
In mathematics, a stereographic projection is a perspective transform, perspective projection of the sphere, through a specific point (geometry), point on the sphere (the ''pole'' or ''center of projection''), onto a plane (geometry), plane (th ...
Permutohedron
Just as thetruncated octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
is the permutohedron
In mathematics, the permutohedron (also spelled permutahedron) of order is an -dimensional polytope embedded in an -dimensional space. Its vertex (geometry), vertex coordinates (labels) are the permutations of the first natural numbers. The edg ...
of order 4, the omnitruncated 5-cell is the permutohedron of order 5.
The omnitruncated 5-cell is a zonotope
In geometry, a zonohedron is a convex polyhedron that is point symmetry, centrally symmetric, every face of which is a polygon that is centrally symmetric (a zonogon). Any zonohedron may equivalently be described as the Minkowski addition, Minkows ...
, the Minkowski sum
In geometry, the Minkowski sum of two sets of position vectors ''A'' and ''B'' in Euclidean space is formed by adding each vector in ''A'' to each vector in ''B'':
A + B = \
The Minkowski difference (also ''Minkowski subtraction'', ''Minkowsk ...
of five line segments parallel to the five lines through the origin and the five vertices of the 5-cell.
Tessellations
Theomnitruncated 5-cell honeycomb
In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb. It is composed of 5-cells and rectified 5-cells facets in a ratio of 1:1. Struct ...
can tessellate 4-dimensional space by translational copies of this cell, each with 3 hypercells around each face. This honeycomb's Coxeter diagram
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
is . Unlike the analogous honeycomb in three dimensions, the bitruncated cubic honeycomb
The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space made up of truncated octahedron, truncated octahedra (or, equivalently, Bitruncation (geometry), bitruncated cubes). It has 4 ...
which has three different Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.
Construction process ...
s, this honeycomb has only one such construction.
Symmetry
The omnitruncated 5-cell has extended pentachoric symmetry, , order 240. Thevertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
of the omnitruncated 5-cell represents the Goursat tetrahedron
In geometry, a Goursat tetrahedron is a tetrahedron, tetrahedral fundamental domain of a Wythoff construction. Each tetrahedral face represents a reflection hyperplane on 3-dimensional surfaces: the 3-sphere, Euclidean 3-space, and hyperbolic 3-spa ...
of the ,3,3Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...
. The extended symmetry comes from a 2-fold rotation across the middle order-3 branch, and is represented more explicitly as +[3,3,3.
:
Coordinates
TheCartesian coordinate
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
s of the vertices of an origin-centered omnitruncated 5-cell having edge length 2 are:
{, class=wikitable
,
:
:
:
:
:
:
:
:
:
,
:
:
:
:
:
:
:
,
:
:
:
:
:
:
:
These vertices can be more simply obtained in 5-space as the 120 permutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
s of (0,1,2,3,4).
This construction is from the positive orthant
In geometry, an orthant or hyperoctant is the analogue in ''n''-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions.
In general an orthant in ''n''-dimensions can be considered the intersection of ''n'' mutu ...
facet
Facets () are flat faces on geometric shapes. The organization of naturally occurring facets was key to early developments in crystallography, since they reflect the underlying symmetry of the crystal structure. Gemstones commonly have facets cu ...
of the runcicantitruncated 5-orthoplex, t0,1,2,3{3,3,3,4}, .
Related polytopes
Nonuniform variants with ,3,3symmetry and two types of truncated octahedra can be doubled by placing the two types of truncated octahedra on each other to produce a nonuniform polychoron with 10truncated octahedra
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 ...
, two types of 40 hexagonal prism
In geometry, the hexagonal prism is a Prism (geometry), prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 face (geometry), faces, 18 Edge (geometry), edges, and 12 vertex (geometry), vertices..
As a semiregular polyhedro ...
s (20 ditrigonal prisms and 20 ditrigonal trapezoprisms), two kinds of 90 rectangular trapezoprisms (30 with ''D2d'' symmetry and 60 with ''C2v'' symmetry), and 240 vertices. Its vertex figure is an irregular triangular bipyramid
A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of a t ...
.

Vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
This polychoron can then be alternated to produce another nonuniform polychoron with 10 icosahedra, two types of 40 octahedra
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
(20 with ''S6'' symmetry and 20 with ''D3'' symmetry), three kinds of 210 tetrahedra
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
(30 tetragonal disphenoids, 60 phyllic disphenoids, and 120 irregular tetrahedra), and 120 vertices. It has a symmetry of 3,3,3
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pentahedroid, tetrahedral ...
sup>+], order 120.

Vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
Full snub 5-cell
 The full snub 5-cell or omnisnub 5-cell, defined as an Alternation (geometry), alternation of the omnitruncated 5-cell, cannot be made uniform, but it can be given Coxeter diagram , and
The full snub 5-cell or omnisnub 5-cell, defined as an Alternation (geometry), alternation of the omnitruncated 5-cell, cannot be made uniform, but it can be given Coxeter diagram , and symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
+, order 120, and constructed from 90 cells: 10 icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical tha ...
s, 20 octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
s, and 60 tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
s filling the gaps at the deleted vertices. It has 300 faces (triangles), 270 edges, and 60 vertices.
Topologically, under its highest symmetry, +, the 10 icosahedra have ''T'' (chiral tetrahedral) symmetry, while the 20 octahedra have ''D3'' symmetry and the 60 tetrahedra have ''C2'' symmetry.
Related polytopes
These polytopes are a part of a family of 9Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedron, uniform polyhedra, and faces are regular polygons.
There are 47 non-Prism (geometry), prism ...
constructed from the ,3,3Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...
.
Notes
References
*H.S.M. Coxeter
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
:
** H.S.M. Coxeter, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973
** Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995wiley.com
*** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380–407, MR 2,10*** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559–591*** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3–45* Norman Johnson ''Uniform Polytopes'', Manuscript (1991) ** N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. * * o3x3x3o - spid, x3x3o3x - prip, x3x3x3x - gippid {{Polytopes Uniform 4-polytopes