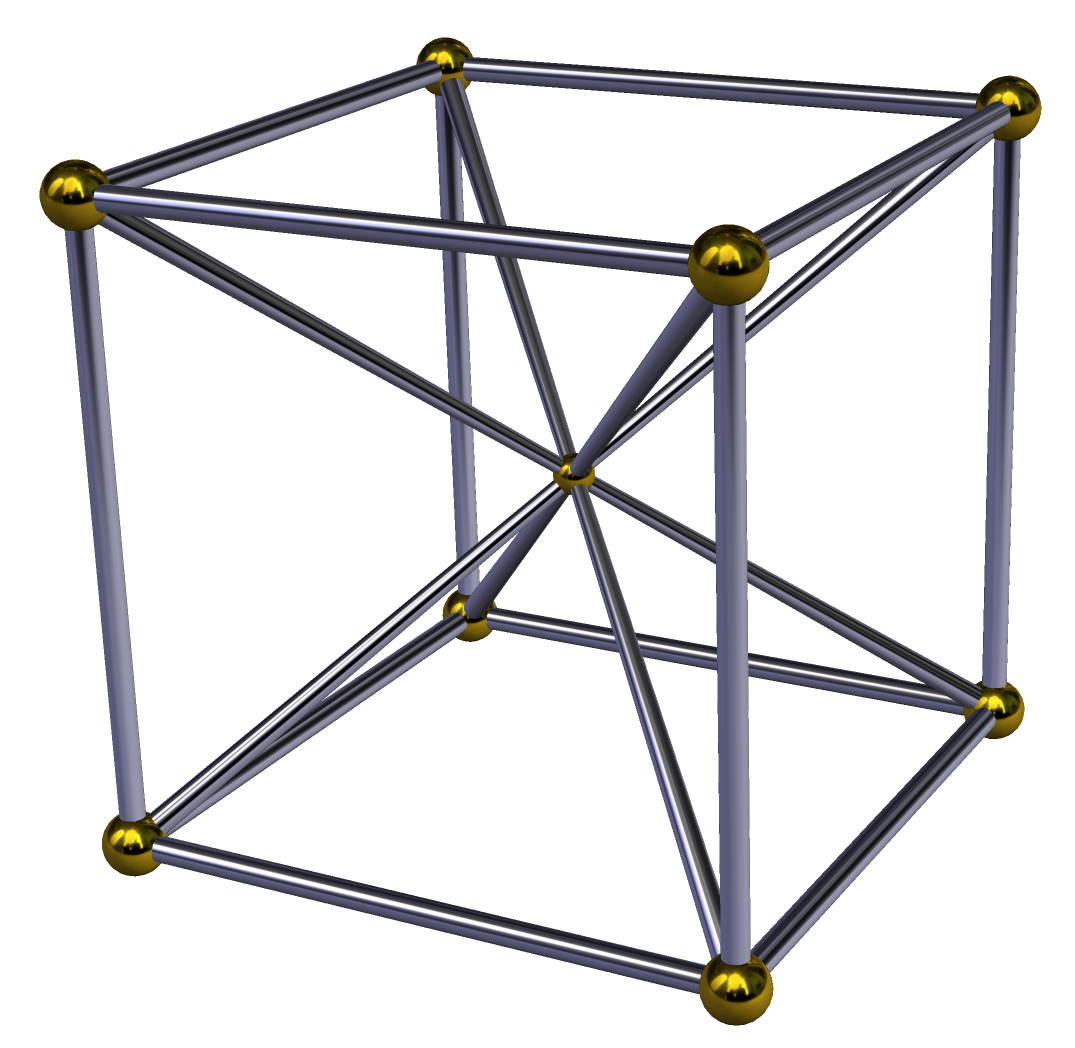
Octahedral Pyramid on:
[Wikipedia]
[Google]
[Amazon]
In 4-dimensional
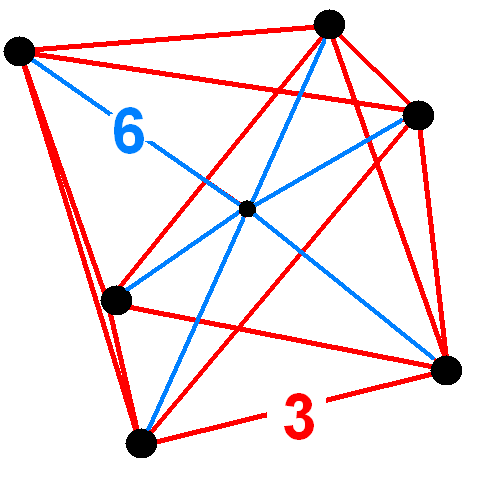 The graph of the octahedral pyramid is the only possible minimal counterexample to
The graph of the octahedral pyramid is the only possible minimal counterexample to


Axial-Symmetrical Edge Facetings of Uniform Polyhedra
4-polytopes {{Polychora-stub
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, the octahedral pyramid is bounded by one octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at e ...
on the base and 8 triangular pyramid cells which meet at the apex. Since an octahedron has a circumradius divided by edge length less than one, the triangular pyramids can be made with regular faces (as regular tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ...
s) by computing the appropriate height.
Having all regular cells, it is a Blind polytope In geometry, a Blind polytope is a convex polytope composed of regular polytope facets.
The category was named after the German couple Gerd and Roswitha Blind, who described them in a series of papers beginning in 1979.
It generalizes the set of sem ...
. Two copies can be augmented to make an octahedral bipyramid
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mi ...
which is also a Blind polytope.
Occurrences of the octahedral pyramid
The regular16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the m ...
has ''octahedral pyramids'' around every vertex, with the octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at e ...
passing through the center of the 16-cell. Therefore placing two regular octahedral pyramids base to base constructs a 16-cell. The 16-cell tessellates 4-dimensional space as the 16-cell honeycomb.
Exactly 24 regular octahedral pyramids will fit together around a vertex in four-dimensional space (the apex of each pyramid). This construction yields a 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oc ...
with octahedral bounding cells, surrounding a central vertex with 24 edge-length long radii. The 4-dimensional content of a unit-edge-length 24-cell is 2, so the content of the regular octahedral pyramid is 1/12. The 24-cell tessellates 4-dimensional space as the 24-cell honeycomb.
The octahedral pyramid is the vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines ...
for a truncated 5-orthoplex, .
: The graph of the octahedral pyramid is the only possible minimal counterexample to
The graph of the octahedral pyramid is the only possible minimal counterexample to Negami's conjecture
In graph theory, a planar cover of a finite graph ''G'' is a finite covering graph of ''G'' that is itself a planar graph. Every graph that can be embedded into the projective plane has a planar cover; an unsolved conjecture of Seiya Negami state ...
, that the connected graphs with planar covers are themselves projective-planar.
Other polytopes
Cubic pyramid
The dual to the octahedral pyramid is acubic pyramid
In 4-dimensional geometry, the cubic pyramid is bounded by one cube on the base and 6 square pyramid cell (mathematics), cells which meet at the apex. Since a cube has a circumradius divided by edge length less than one, the square pyramids can be ...
, seen as a cubic base and 6 square pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has symmetry. If all edge lengths are equal, it is an equilateral square pyramid ...
s meeting at an apex.
:
Square-pyramidal pyramid
The square-pyramidal pyramid, ( ) ∨ ) ∨ is a bisected octahedral pyramid. It has asquare pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has symmetry. If all edge lengths are equal, it is an equilateral square pyramid ...
base, and 4 tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ...
s along with another one more square pyramid meeting at the apex. It can also be seen in an edge-centered projection as a square bipyramid with four tetrahedra wrapped around the common edge. If the height of the two apexes are the same, it can be given a higher symmetry name ) ∨ ( )∨ = ∨ , joining an edge to a perpendicular square.
The ''square-pyramidal pyramid'' can be distorted into a ''rectangular-pyramidal pyramid'', ∨ ×
The multiplication sign, also known as the times sign or the dimension sign, is the symbol , used in mathematics to denote the multiplication operation and its resulting product. While similar to a lowercase X (), the form is properly a four ...
or a ''rhombic-pyramidal pyramid'', ∨ + or other lower symmetry forms.
The ''square-pyramidal pyramid'' exists as a vertex figure in uniform polytopes of the form , including the bitruncated 5-orthoplex and bitruncated tesseractic honeycomb.
:

References
External links
* * ** * Richard KlitzingAxial-Symmetrical Edge Facetings of Uniform Polyhedra
4-polytopes {{Polychora-stub