nuclear structure on:
[Wikipedia]
[Google]
[Amazon]
Understanding the structure of the
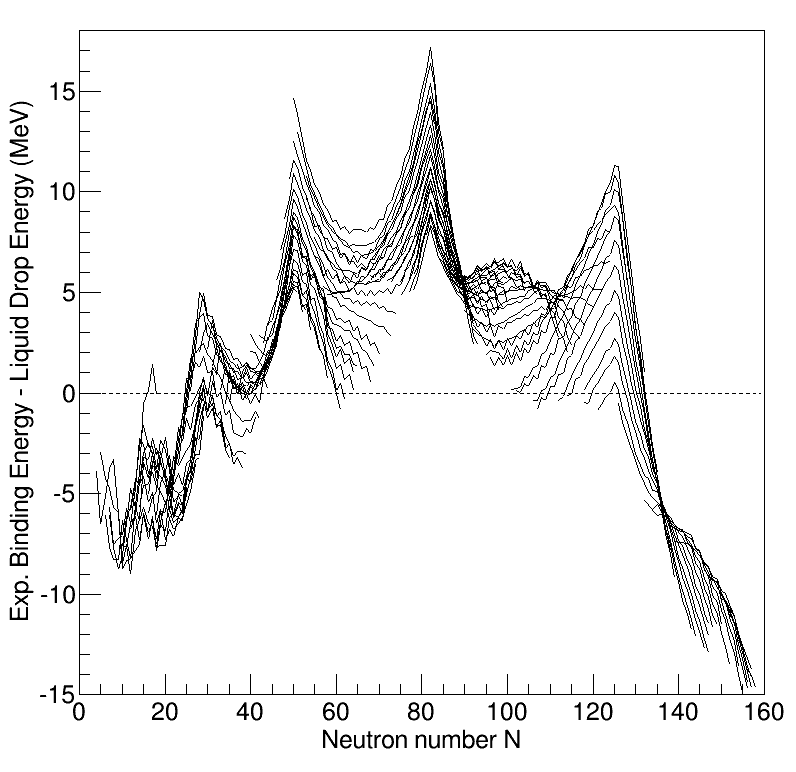 Systematic measurements of the
Systematic measurements of the
Institut de Physique Nucléaire (IPN), France
* Facility for Antiproton and Ion Research (FAIR), Germany
Gesellschaft für Schwerionenforschung (GSI), Germany
Joint Institute for Nuclear Research (JINR), Russia
Argonne National Laboratory (ANL), USA
National Superconducting Cyclotron Laboratory, Michigan State University, USA
Facility for Rare Isotope Beams, Michigan State University, USA
;French
Institut de Physique Nucléaire (IPN), France
Centre de Spectrométrie Nucléaire et de Spectrométrie de Masse (CSNSM), France
Service de Physique Nucléaire CEA/DAM, France
Institut National de Physique Nucléaire et de Physique des Particules (In2p3), France
Grand Accélérateur National d'Ions Lourds (GANIL), France
Commissariat à l'Energie Atomique (CEA), France
* '
The LIVEChart of Nuclides - IAEA
'' {{see also, Nuclear physics#External links Nuclear physics Quantum mechanics
atomic nucleus
The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford at the Department_of_Physics_and_Astronomy,_University_of_Manchester , University of Manchester ...
is one of the central challenges in nuclear physics
Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter.
Nuclear physics should not be confused with atomic physics, which studies th ...
.
Models
The cluster model
The cluster model describes the nucleus as a molecule-like collection of proton-neutron groups (e.g., alpha particles) with one or more valence neutrons occupying molecular orbitals.The liquid drop model
The liquid drop model is one of the first models of nuclear structure, proposed by Carl Friedrich von Weizsäcker in 1935. It describes the nucleus as a semiclassical fluid made up ofneutron
The neutron is a subatomic particle, symbol or , that has no electric charge, and a mass slightly greater than that of a proton. The Discovery of the neutron, neutron was discovered by James Chadwick in 1932, leading to the discovery of nucle ...
s and proton
A proton is a stable subatomic particle, symbol , Hydron (chemistry), H+, or 1H+ with a positive electric charge of +1 ''e'' (elementary charge). Its mass is slightly less than the mass of a neutron and approximately times the mass of an e ...
s, with an internal repulsive electrostatic force proportional to the number of protons. The quantum mechanical nature of these particles appears via the Pauli exclusion principle, which states that no two nucleons of the same kind can be at the same state
State most commonly refers to:
* State (polity), a centralized political organization that regulates law and society within a territory
**Sovereign state, a sovereign polity in international law, commonly referred to as a country
**Nation state, a ...
. Thus the fluid is actually what is known as a Fermi liquid
Fermi liquid theory (also known as Landau's Fermi-liquid theory) is a theoretical model of interacting fermions that describes the normal state of the conduction electrons in most metals at sufficiently low temperatures. The theory describes the ...
.
In this model, the binding energy of a nucleus with protons and neutrons is given by
:
where is the total number of nucleons
In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number.
Until the 1960s, nucleons were thought to be ele ...
(Mass Number
The mass number (symbol ''A'', from the German word: ''Atomgewicht'', "atomic weight"), also called atomic mass number or nucleon number, is the total number of protons and neutrons (together known as nucleons) in an atomic nucleus. It is appro ...
). The terms proportional to and represent the volume and surface energy of the liquid drop, the term proportional to represents the electrostatic energy, the term proportional to represents the Pauli exclusion principle and the last term is the pairing term, which lowers the energy for even numbers of protons or neutrons.
The coefficients and the strength of the pairing term may be estimated theoretically, or fit to data.
This simple model reproduces the main features of the binding energy
In physics and chemistry, binding energy is the smallest amount of energy required to remove a particle from a system of particles or to disassemble a system of particles into individual parts. In the former meaning the term is predominantly use ...
of nuclei.
The assumption of nucleus as a drop of Fermi liquid
Fermi liquid theory (also known as Landau's Fermi-liquid theory) is a theoretical model of interacting fermions that describes the normal state of the conduction electrons in most metals at sufficiently low temperatures. The theory describes the ...
is still widely used in the form of Finite Range Droplet Model (FRDM), due to the possible good reproduction of nuclear binding energy on the whole chart, with the necessary accuracy for predictions of unknown nuclei.
The shell model
The expression "shell model" is ambiguous in that it refers to two different items. It was previously used to describe the existence of nucleon shells according to an approach closer to what is now called mean field theory. Nowadays, it refers to a formalism analogous to the configuration interaction formalism used inquantum chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions ...
.
Introduction to the shell concept
 Systematic measurements of the
Systematic measurements of the binding energy
In physics and chemistry, binding energy is the smallest amount of energy required to remove a particle from a system of particles or to disassemble a system of particles into individual parts. In the former meaning the term is predominantly use ...
of atomic nuclei show systematic deviations with respect to those estimated from the liquid drop model. In particular, some nuclei having certain values for the number of protons and/or neutrons are bound more tightly together than predicted by the liquid drop model. These nuclei are called singly/doubly magic. This observation led scientists to assume the existence of a shell structure of nucleon
In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number.
Until the 1960s, nucleons were thought to be ele ...
s (protons and neutrons) within the nucleus, like that of electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
s within atoms.
Indeed, nucleons are quantum objects. Strictly speaking, one should not speak of energies of individual nucleons, because they are all correlated with each other. However, as an approximation one may envision an average nucleus, within which nucleons propagate individually. Owing to their quantum character, they may only occupy ''discrete'' energy level
A quantum mechanics, quantum mechanical system or particle that is bound state, bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical mechanics, classical pa ...
s. These levels are by no means uniformly distributed; some intervals of energy are crowded, and some are empty, generating a gap in possible energies. A shell is such a set of levels separated from the other ones by a wide empty gap.
The energy levels are found by solving the Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
for a single nucleon moving in the average potential generated by all other nucleons. Each level may be occupied by a nucleon, or empty. Some levels accommodate several different quantum states with the same energy; they are said to be ''degenerate''. This occurs in particular if the average nucleus exhibits a certain symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
, like a spherical shape.
The concept of shells allows one to understand why some nuclei are bound more tightly than others. This is because two nucleons of the same kind cannot be in the same state ( Pauli exclusion principle). Werner Heisenberg
Werner Karl Heisenberg (; ; 5 December 1901 – 1 February 1976) was a German theoretical physicist, one of the main pioneers of the theory of quantum mechanics and a principal scientist in the German nuclear program during World War II.
He pub ...
extended the principle of Pauli exclusion to nucleons, via the introduction of the iso-spin concept. Nucleons are thought to be composed of two kind of particles, the neutron and the proton that differ through their intrinsic property, associated with their iso-spin quantum number. This concept enables the explanation of the bound state of Deuterium
Deuterium (hydrogen-2, symbol H or D, also known as heavy hydrogen) is one of two stable isotopes of hydrogen; the other is protium, or hydrogen-1, H. The deuterium nucleus (deuteron) contains one proton and one neutron, whereas the far more c ...
, in which the proton and neutron can couple their spin and iso-spin in two different manners. So the lowest-energy state of the nucleus is one where nucleons fill all energy levels from the bottom up to some level. Nuclei that exhibit an odd number of either protons or neutrons are less bound than nuclei with even number. A nucleus with full shells is exceptionally stable, as will be explained.
As with electrons in the electron shell
In chemistry and atomic physics, an electron shell may be thought of as an orbit that electrons follow around an atom's nucleus. The closest shell to the nucleus is called the "1 shell" (also called the "K shell"), followed by the "2 shell" (o ...
model, protons in the outermost shell are relatively loosely bound to the nucleus if there are only few protons in that shell, because they are farthest from the center of the nucleus. Therefore, nuclei which have a full outer proton shell will be more tightly bound and have a higher binding energy than other nuclei with a similar total number of protons. This is also true for neutrons.
Furthermore, the energy needed to excite the nucleus (i.e. moving a nucleon to a higher, previously unoccupied level) is exceptionally high in such nuclei. Whenever this unoccupied level is the next after a full shell, the only way to excite the nucleus is to raise one nucleon ''across the gap'', thus spending a large amount of energy. Otherwise, if the highest occupied energy level lies in a partly filled shell, much less energy is required to raise a nucleon to a higher state in the same shell.
Some evolution of the shell structure observed in stable nuclei is expected away from the valley of stability. For example, observations of unstable isotopes
Isotopes are distinct nuclear species (or ''nuclides'') of the same chemical element. They have the same atomic number (number of protons in their nuclei) and position in the periodic table (and hence belong to the same chemical element), but ...
have shown shifting and even a reordering of the single particle levels of which the shell structure is composed. This is sometimes observed as the creation of an island of inversion or in the reduction of excitation energy gaps above the traditional magic numbers.
Basic hypotheses
Some basic hypotheses are made in order to give a precise conceptual framework to the shell model: *The atomic nucleus is aquantum
In physics, a quantum (: quanta) is the minimum amount of any physical entity (physical property) involved in an interaction. The fundamental notion that a property can be "quantized" is referred to as "the hypothesis of quantization". This me ...
''n''-body system.
*The internal motion of nucleons within the nucleus is non-relativistic, and their behavior is governed by the Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
.
*Nucleons are considered to be pointlike, without any internal structure.
Brief description of the formalism
The general process used in the shell model calculations is the following. First aHamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
for the nucleus is defined. Usually, for computational practicality, only one- and two-body terms are taken into account in this definition. The interaction is an effective theory: it contains free parameters which have to be fitted with experimental data.
The next step consists in defining a basis of single-particle states, i.e. a set of wavefunction
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
s describing all possible nucleon states. Most of the time, this basis is obtained via a Hartree–Fock computation. With this set of one-particle states, Slater determinants are built, that is, wavefunctions for ''Z'' proton variables or ''N'' neutron variables, which are antisymmetrized products of single-particle wavefunctions (antisymmetrized meaning that under exchange of variables for any pair of nucleons, the wavefunction only changes sign).
In principle, the number of quantum state
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system ...
s available for a single nucleon at a finite energy is finite, say ''n''. The number of nucleons in the nucleus must be smaller than the number of available states, otherwise the nucleus cannot hold all of its nucleons. There are thus several ways to choose ''Z'' (or ''N'') states among the ''n'' possible. In combinatorial mathematics, the number of choices of ''Z'' objects among ''n'' is the binomial coefficient
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers and is written \tbinom. It is the coefficient of the t ...
C. If ''n'' is much larger than ''Z'' (or ''N''), this increases roughly like ''n''''Z''. Practically, this number becomes so large that every computation is impossible for ''A''=''N''+''Z'' larger than 8.
To obviate this difficulty, the space of possible single-particle states is divided into core and valence, by analogy with chemistry (see core electron and valence electron
In chemistry and physics, valence electrons are electrons in the outermost shell of an atom, and that can participate in the formation of a chemical bond if the outermost shell is not closed. In a single covalent bond, a shared pair forms with b ...
). The core is a set of single-particles which are assumed to be inactive, in the sense that they are the well bound lowest-energy states, and that there is no need to reexamine their situation. They do not appear in the Slater determinants, contrary to the states in the valence space, which is the space of all single-particle states ''not in the core'', but possibly to be considered in the choice of the build of the (''Z''-) ''N''-body wavefunction. The set of all possible Slater determinants in the valence space defines a basis for (''Z''-) ''N''-body states.
The last step consists in computing the matrix of the Hamiltonian within this basis, and to diagonalize it. In spite of the reduction of the dimension of the basis owing to the fixation of the core, the matrices to be diagonalized reach easily dimensions of the order of 109, and demand specific diagonalization techniques.
The shell model calculations give in general an excellent fit with experimental data. They depend however strongly on two main factors:
*The way to divide the single-particle space into core and valence.
*The effective nucleon–nucleon interaction.
Mean field theories
The independent-particle model (IPM)
The interaction between nucleons, which is a consequence ofstrong interaction
In nuclear physics and particle physics, the strong interaction, also called the strong force or strong nuclear force, is one of the four known fundamental interaction, fundamental interactions. It confines Quark, quarks into proton, protons, n ...
s and binds the nucleons within the nucleus, exhibits the peculiar behaviour of having a finite range: it vanishes when the distance between two nucleons becomes too large; it is attractive at medium range, and repulsive at very small range. This last property correlates with the Pauli exclusion principle according to which two fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles i ...
s (nucleons are fermions) cannot be in the same quantum state. This results in a very large mean free path
In physics, mean free path is the average distance over which a moving particle (such as an atom, a molecule, or a photon) travels before substantially changing its direction or energy (or, in a specific context, other properties), typically as a ...
predicted for a nucleon within the nucleus.
The main idea of the Independent Particle approach is that a nucleon moves inside a certain potential well (which keeps it bound to the nucleus) independently from the other nucleons. This amounts to replacing an ''N''-body problem (''N'' particles interacting) by ''N'' single-body problems. This essential simplification of the problem is the cornerstone of mean field theories. These are also widely used in atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. Atomic physics typically refers to the study of atomic structure and the interaction between atoms. It is primarily concerned wit ...
, where electrons move in a mean field due to the central nucleus and the electron cloud itself.
The independent particle model and mean field theories (we shall see that there exist several variants) have a great success in describing the properties of the nucleus starting from an effective interaction or an effective potential, thus are a basic part of atomic nucleus theory. One should also notice that they are modular enough, in that it is quite easy to extend the model to introduce effects such as nuclear pairing, or collective motions of the nucleon like rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
, or vibration
Vibration () is a mechanical phenomenon whereby oscillations occur about an equilibrium point. Vibration may be deterministic if the oscillations can be characterised precisely (e.g. the periodic motion of a pendulum), or random if the os ...
, adding the corresponding energy terms in the formalism. This implies that in many representations, the mean field is only a starting point for a more complete description which introduces correlations reproducing properties like collective excitations and nucleon transfer.
Nuclear potential and effective interaction
A large part of the practical difficulties met in mean field theories is the definition (or calculation) of thepotential
Potential generally refers to a currently unrealized ability. The term is used in a wide variety of fields, from physics to the social sciences to indicate things that are in a state where they are able to change in ways ranging from the simple r ...
of the mean field itself. One can very roughly distinguish between two approaches:
*The phenomenological approach is a parameterization of the nuclear potential by an appropriate mathematical function. Historically, this procedure was applied with the greatest success by Sven Gösta Nilsson, who used as a potential a (deformed) harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive const ...
potential. The most recent parameterizations are based on more realistic functions, which account more accurately for scattering experiments, for example. In particular the form known as the Woods–Saxon potential can be mentioned.
*The self-consistent or Hartree–Fock approach aims to deduce mathematically the nuclear potential from an effective nucleon–nucleon interaction. This technique implies a solution of the Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
in an iterative fashion, starting from an ansatz wavefunction and improving it variationally, since the potential depends there upon the wavefunctions to be determined. The latter are written as Slater determinants.
In the case of the Hartree–Fock approaches, the trouble is not to find the mathematical function which describes best the nuclear potential, but that which describes best the nucleon–nucleon interaction. Indeed, in contrast with atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. Atomic physics typically refers to the study of atomic structure and the interaction between atoms. It is primarily concerned wit ...
where the interaction is known (it is the Coulomb
The coulomb (symbol: C) is the unit of electric charge in the International System of Units (SI).
It is defined to be equal to the electric charge delivered by a 1 ampere current in 1 second, with the elementary charge ''e'' as a defining c ...
interaction), the nucleon–nucleon interaction within the nucleus is not known analytically.
There are two main reasons for this fact. First, the strong interaction acts essentially among the quark
A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nucleus, atomic nuclei ...
s forming the nucleons. The nucleon–nucleon interaction in vacuum is a mere ''consequence'' of the quark–quark interaction. While the latter is well understood in the framework of the Standard Model
The Standard Model of particle physics is the Scientific theory, theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions – excluding gravity) in the unive ...
at high energies, it is much more complicated in low energies due to color confinement
In quantum chromodynamics (QCD), color confinement, often simply called confinement, is the phenomenon that color-charged particles (such as quarks and gluons) cannot be isolated, and therefore cannot be directly observed in normal conditions b ...
and asymptotic freedom. Thus there is yet no fundamental theory allowing one to deduce the nucleon–nucleon interaction from the quark–quark interaction. Furthermore, even if this problem were solved, there would remain a large difference between the ideal (and conceptually simpler) case of two nucleons interacting in vacuum, and that of these nucleons interacting in the nuclear matter. To go further, it was necessary to invent the concept of effective interaction. The latter is basically a mathematical function with several arbitrary parameters, which are adjusted to agree with experimental data.
Most modern interaction are zero-range so they act only when the two nucleons are in contact, as introduced by Tony Skyrme. In a seminal paper by Dominique Vautherin and David M. Brink it was demonstrated that a Skyrme force that is density dependent can reproduce basic properties of atomic nuclei. Other commonly used interaction is the finite range Gogny force,
The self-consistent approaches of the Hartree–Fock type
In the Hartree–Fock approach of the ''n''-body problem, the starting point is aHamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
containing ''n'' kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
terms, and potential terms. As mentioned before, one of the mean field theory hypotheses is that only the two-body interaction is to be taken into account. The potential term of the Hamiltonian represents all possible two-body interactions in the set of ''n'' fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles i ...
s. It is the first hypothesis.
The second step consists in assuming that the wavefunction
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
of the system can be written as a Slater determinant of one-particle spin-orbitals. This statement is the mathematical translation of the independent-particle model. This is the second hypothesis.
There remains now to determine the components of this Slater determinant, that is, the individual wavefunction
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
s of the nucleons. To this end, it is assumed that the total wavefunction (the Slater determinant) is such that the energy is minimum. This is the third hypothesis.
Technically, it means that one must compute the mean value
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
of the (known) two-body Hamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
on the (unknown) Slater determinant, and impose that its mathematical variation vanishes. This leads to a set of equations where the unknowns are the individual wavefunctions: the Hartree–Fock equations. Solving these equations gives the wavefunctions and individual energy levels of nucleons, and so the total energy of the nucleus and its wavefunction.
This short account of the Hartree–Fock method explains why it is called also the variational approach. At the beginning of the calculation, the total energy is a "function of the individual wavefunctions" (a so-called functional), and everything is then made in order to optimize the choice of these wavefunctions so that the functional has a minimum – hopefully absolute, and not only local. To be more precise, there should be mentioned that the energy is a functional of the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
, defined as the sum of the individual squared wavefunctions. The Hartree–Fock method is also used in atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. Atomic physics typically refers to the study of atomic structure and the interaction between atoms. It is primarily concerned wit ...
and condensed matter physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid State of matter, phases, that arise from electromagnetic forces between atoms and elec ...
as Density Functional Theory, DFT.
The process of solving the Hartree–Fock equations can only be iterative, since these are in fact a Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
in which the potential depends on the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
, that is, precisely on the wavefunction
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
s to be determined. Practically, the algorithm is started with a set of individual grossly reasonable wavefunctions (in general the eigenfunctions of a harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive const ...
). These allow to compute the density, and therefrom the Hartree–Fock potential. Once this done, the Schrödinger equation is solved anew, and so on. The calculation stops – convergence is reached – when the difference among wavefunctions, or energy levels, for two successive iterations is less than a fixed value. Then the mean field potential is completely determined, and the Hartree–Fock equations become standard Schrödinger equations. The corresponding Hamiltonian is then called the Hartree–Fock Hamiltonian.
The relativistic mean field approaches
Born first in the 1970s with the works of John Dirk Walecka on quantum hadrodynamics, the relativistic models of the nucleus were sharpened up towards the end of the 1980s by P. Ring and coworkers. The starting point of these approaches is the relativisticquantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct phy ...
. In this context, the nucleon interactions occur via the exchange of virtual particle
A virtual particle is a theoretical transient particle that exhibits some of the characteristics of an ordinary particle, while having its existence limited by the uncertainty principle, which allows the virtual particles to spontaneously emer ...
s called meson
In particle physics, a meson () is a type of hadronic subatomic particle composed of an equal number of quarks and antiquarks, usually one of each, bound together by the strong interaction. Because mesons are composed of quark subparticles, the ...
s. The idea is, in a first step, to build a Lagrangian containing these interaction terms. Second, by an application of the least action principle, one gets a set of equations of motion. The real particles (here the nucleons) obey the Dirac equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1/2 massive particles, called "Dirac ...
, whilst the virtual ones (here the mesons) obey the Klein–Gordon equations.
In view of the non- perturbative nature of strong interaction, and also since the exact potential form of this interaction between groups of nucleons is relatively badly known, the use of such an approach in the case of atomic nuclei requires drastic approximations. The main simplification consists in replacing in the equations all field terms (which are operators in the mathematical sense) by their mean value
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
(which are functions). In this way, one gets a system of coupled integro-differential equation
In mathematics, an integro-differential equation is an equation that involves both integrals and derivatives of a function (mathematics), function.
General first order linear equations
The general first-order, linear (only with respect to the t ...
s, which can be solved numerically, if not analytically.
The interacting boson model
The interacting boson model (IBM) is a model in nuclear physics in which nucleons are represented as pairs, each of them acting as a boson particle, with integral spin of 0, 2 or 4. This makes calculations feasible for larger nuclei. There are several branches of this model - in one of them (IBM-1) one can group all types of nucleons in pairs, in others (for instance - IBM-2) one considers protons and neutrons in pairs separately.Spontaneous breaking of symmetry in nuclear physics
One of the focal points of all physics issymmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
. The nucleon–nucleon interaction and all effective interactions used in practice have certain symmetries. They are invariant by translation
Translation is the communication of the semantics, meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The English la ...
(changing the frame of reference so that directions are not altered), by rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
(turning the frame of reference around some axis), or parity (changing the sense of axes) in the sense that the interaction does not change under any of these operations. Nevertheless, in the Hartree–Fock approach, solutions which are not invariant under such a symmetry can appear. One speaks then of spontaneous symmetry breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion o ...
.
Qualitatively, these spontaneous symmetry breakings can be explained in the following way: in the mean field theory, the nucleus is described as a set of independent particles. Most additional correlations among nucleons which do not enter the mean field are neglected. They can appear however by a breaking of the symmetry of the mean field Hamiltonian, which is only approximate. If the density used to start the iterations of the Hartree–Fock process breaks certain symmetries, the final Hartree–Fock Hamiltonian may break these symmetries, if it is advantageous to keep these broken from the point of view of the total energy.
It may also converge towards a symmetric solution. In any case, if the final solution breaks the symmetry, for example, the rotational symmetry, so that the nucleus appears not to be spherical, but elliptic, all configurations deduced from this deformed nucleus by a rotation are just as good solutions for the Hartree–Fock problem. The ground state of the nucleus is then ''degenerate''.
A similar phenomenon happens with the nuclear pairing, which violates the conservation of the number of baryons (see below).
Extensions of the mean field theories
Nuclear pairing phenomenon
The most common extension to mean field theory is the nuclear pairing. Nuclei with an even number of nucleons are systematically more bound than those with an odd one. This implies that each nucleon binds with another one to form a pair, consequently the system cannot be described as independent particles subjected to a common mean field. When the nucleus has an even number of protons and neutrons, each one of them finds a partner. To excite such a system, one must at least use such an energy as to break a pair. Conversely, in the case of odd number of protons or neutrons, there exists an unpaired nucleon, which needs less energy to be excited. This phenomenon is closely analogous to that of Type 1superconductivity
Superconductivity is a set of physical properties observed in superconductors: materials where Electrical resistance and conductance, electrical resistance vanishes and Magnetic field, magnetic fields are expelled from the material. Unlike an ord ...
in solid state physics. The first theoretical description of nuclear pairing was proposed at the end of the 1950s by Aage Bohr, Ben Mottelson, and David Pines (which contributed to the reception of the Nobel Prize in Physics in 1975 by Bohr and Mottelson). It was close to the BCS theory
In physics, the Bardeen–Cooper–Schrieffer (BCS) theory (named after John Bardeen, Leon Cooper, and John Robert Schrieffer) is the first microscopic theory of superconductivity since Heike Kamerlingh Onnes's 1911 discovery. The theory descr ...
of Bardeen, Cooper and Schrieffer, which accounts for metal superconductivity. Theoretically, the pairing phenomenon as described by the BCS theory combines with the mean field theory: nucleons are both subject to the mean field potential and to the pairing interaction.
The Hartree–Fock–Bogolyubov (HFB) method is a more sophisticated approach, enabling one to consider the pairing and mean field interactions consistently on equal footing. HFB is now the de facto standard in the mean field treatment of nuclear systems.
Symmetry restoration
Peculiarity of mean field methods is the calculation of nuclear property by explicit symmetry breaking. The calculation of the mean field with self-consistent methods (e.g. Hartree-Fock), breaks rotational symmetry, and the calculation of pairing property breaks particle-number. Several techniques for symmetry restoration by projecting on good quantum numbers have been developed.Particle vibration coupling
Mean field methods (eventually considering symmetry restoration) are a good approximation for the ground state of the system, even postulating a system of independent particles. Higher-order corrections consider the fact that the particles interact together by the means of correlation. These correlations can be introduced taking into account the coupling of independent particle degrees of freedom, low-energy collective excitation of systems with even number of protons and neutrons. In this way, excited states can be reproduced by the means of random phase approximation (RPA), also eventually consistently calculating corrections to the ground state (e.g. by the means of nuclear field theory).See also
* Nuclear magnetic moment * CHARISSA, a nuclear structure research collaborationFurther reading
General audience
*James M. Cork; ''Radioactivité & physique nucléaire'', Dunod (1949).Introductory texts
*Luc Valentin; ''Le monde subatomique - Des quarks aux centrales nucléaires'', Hermann (1986). *Luc Valentin; ''Noyaux et particules - Modèles et symétries'', Hermann (1997). *David Halliday; ''Introductory Nuclear Physics'', Wiley & Sons (1957). *Kenneth Krane; ''Introductory Nuclear Physics'', Wiley & Sons (1987). *Carlos Bertulani; ''Nuclear Physics in a Nutshell'', Princeton University Press (2007).Fundamental texts
* Peter E. Hodgson; ''Nuclear Reactions and Nuclear Structure''. Oxford University Press (1971).'' *Irving Kaplan; ''Nuclear physics'', the Addison-Wesley Series in Nuclear Science & Engineering, Addison-Wesley (1956). 2nd edition (1962). *A. Bohr & B. Mottelson; ''Nuclear Structure'', 2 vol., Benjamin (1969–1975). Volume 1 : ''Single Particle Motion''; Volume 2 : ''Nuclear Deformations''. Réédité par World Scientific Publishing Company (1998), . *P. Ring & P. Schuck; ''The nuclear many-body problem'', Springer Verlag (1980), *A. de Shalit & H. Feshbach; ''Theoretical Nuclear Physics'', 2 vol., John Wiley & Sons (1974). Volume 1: ''Nuclear Structure''; Volume 2: ''Nuclear Reactions'',References
External links
;EnglishInstitut de Physique Nucléaire (IPN), France
* Facility for Antiproton and Ion Research (FAIR), Germany
Gesellschaft für Schwerionenforschung (GSI), Germany
Joint Institute for Nuclear Research (JINR), Russia
Argonne National Laboratory (ANL), USA
National Superconducting Cyclotron Laboratory, Michigan State University, USA
Facility for Rare Isotope Beams, Michigan State University, USA
;French
Institut de Physique Nucléaire (IPN), France
Centre de Spectrométrie Nucléaire et de Spectrométrie de Masse (CSNSM), France
Service de Physique Nucléaire CEA/DAM, France
Institut National de Physique Nucléaire et de Physique des Particules (In2p3), France
Grand Accélérateur National d'Ions Lourds (GANIL), France
Commissariat à l'Energie Atomique (CEA), France
* '
The LIVEChart of Nuclides - IAEA
'' {{see also, Nuclear physics#External links Nuclear physics Quantum mechanics