Nonlinear Control on:
[Wikipedia]
[Google]
[Amazon]
Nonlinear control theory is the area of control theory which deals with systems that are nonlinear, time-variant, or both. Control theory is an interdisciplinary branch of engineering and
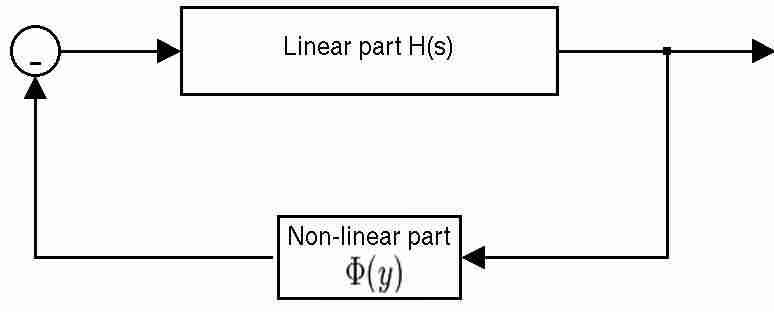 An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e.
Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.
The linear part can be characterized by four matrices (''A'',''B'',''C'',''D''), while the nonlinear part is Φ(''y'') with
An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e.
Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.
The linear part can be characterized by four matrices (''A'',''B'',''C'',''D''), while the nonlinear part is Φ(''y'') with
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
that is concerned with the behavior of dynamical systems with inputs, and how to modify the output by changes in the input using feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled ...
, feedforward
Feedforward is the provision of context of what one wants to communicate prior to that communication. In purposeful activity, feedforward creates an expectation which the actor anticipates. When expected experience occurs, this provides confirmato ...
, or signal filtering. The system to be controlled is called the " plant". One way to make the output of a system follow a desired reference signal is to compare the output of the plant to the desired output, and provide feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled ...
to the plant to modify the output to bring it closer to the desired output.
Control theory is divided into two branches. Linear control theory applies to systems made of devices which obey the superposition principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So tha ...
. They are governed by linear differential equations. A major subclass is systems which in addition have parameters which do not change with time, called '' linear time invariant'' (LTI) systems. These systems can be solved by powerful frequency domain mathematical techniques of great generality, such as the Laplace transform, Fourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, ...
, Z transform, Bode plot, root locus, and Nyquist stability criterion.
Nonlinear control theory covers a wider class of systems that do not obey the superposition principle. It applies to more real-world systems, because all real control systems are nonlinear. These systems are often governed by nonlinear differential equation
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many oth ...
s. The mathematical techniques which have been developed to handle them are more rigorous and much less general, often applying only to narrow categories of systems. These include limit cycle theory, Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower-dimensional ...
s, Lyapunov stability theory, and describing functions. If only solutions near a stable point are of interest, nonlinear systems can often be linearized by approximating them by a linear system obtained by expanding the nonlinear solution in a series, and then linear techniques can be used. Nonlinear systems are often analyzed using numerical method
In numerical analysis, a numerical method is a mathematical tool designed to solve numerical problems. The implementation of a numerical method with an appropriate convergence check in a programming language is called a numerical algorithm.
Mathem ...
s on computer
A computer is a machine that can be programmed to Execution (computing), carry out sequences of arithmetic or logical operations (computation) automatically. Modern digital electronic computers can perform generic sets of operations known as C ...
s, for example by simulating
A simulation is the imitation of the operation of a real-world process or system over time. Simulations require the use of models; the model represents the key characteristics or behaviors of the selected system or process, whereas the s ...
their operation using a simulation language. Even if the plant is linear, a nonlinear controller can often have attractive features such as simpler implementation, faster speed, more accuracy, or reduced control energy, which justify the more difficult design procedure.
An example of a nonlinear control system is a thermostat
A thermostat is a regulating device component which senses the temperature of a physical system and performs actions so that the system's temperature is maintained near a desired setpoint.
Thermostats are used in any device or system tha ...
-controlled heating system. A building heating system such as a furnace has a nonlinear response to changes in temperature; it is either "on" or "off", it does not have the fine control in response to temperature differences that a proportional (linear) device would have. Therefore, the furnace is off until the temperature falls below the "turn on" setpoint of the thermostat, when it turns on. Due to the heat added by the furnace, the temperature increases until it reaches the "turn off" setpoint of the thermostat, which turns the furnace off, and the cycle repeats. This cycling of the temperature about the desired temperature is called a '' limit cycle'', and is characteristic of nonlinear control systems.
Properties of nonlinear systems
Some properties of nonlinear dynamic systems are * They do not follow the principle of superposition (linearity and homogeneity). * They may have multiple isolated equilibrium points. * They may exhibit properties such as limit cycle, bifurcation, chaos. * Finite escape time: Solutions of nonlinear systems may not exist for all times.Analysis and control of nonlinear systems
There are several well-developed techniques for analyzing nonlinear feedback systems: * Describing function method * Phase plane method * Lyapunov stability analysis *Singular perturbation In mathematics, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero. More precisely, the solution cannot be uniformly approximated by an asymptotic expansion
: ...
method
* The Popov criterion In nonlinear control and stability theory, the Popov criterion is a stability criterion discovered by Vasile M. Popov for the absolute stability of a class of nonlinear systems whose nonlinearity must satisfy an open-sector condition. While the circ ...
and the circle criterion In nonlinear control and stability theory, the circle criterion is a stability criterion for nonlinear time-varying systems. It can be viewed as a generalization of the Nyquist stability criterion for linear time-invariant (LTI) systems.
Overvi ...
for absolute stability
* Center manifold theorem
* Small-gain theorem
In nonlinear systems, the formalism of input-output stability is an important tool in studying the stability of interconnected systems since the gain of a system directly relates to how the norm of a signal increases or decreases as it passes thro ...
* Passivity analysis
Passive may refer to:
* Passive voice, a grammatical voice common in many languages, see also Pseudopassive
* Passive language, a language from which an interpreter works
* Passivity (behavior), the condition of submitting to the influence of ...
Control design techniques for nonlinear systems also exist. These can be subdivided into techniques which attempt to treat the system as a linear system in a limited range of operation and use (well-known) linear design techniques for each region:
* Gain scheduling
Those that attempt to introduce auxiliary nonlinear feedback in such a way that the system can be treated as linear for purposes of control design:
* Feedback linearization
Feedback linearization is a common strategy employed in nonlinear control to control nonlinear systems. Feedback linearization techniques may be applied to nonlinear control systems of the form
where x(t) \in \mathbb^n is the state, u_1(t), ...
And Lyapunov Lyapunov (, in old-Russian often written Лепунов) is a Russian surname that is sometimes also romanized as Ljapunov, Liapunov or Ljapunow. Notable people with the surname include:
* Alexey Lyapunov (1911–1973), Russian mathematician
* Alek ...
based methods:
* Lyapunov redesign In nonlinear control
Nonlinear control theory is the area of control theory which deals with systems that are nonlinear, time-variant, or both. Control theory is an interdisciplinary branch of engineering and mathematics that is concerned wit ...
* Control-Lyapunov function
* Nonlinear damping
* Backstepping
* Sliding mode control
Nonlinear feedback analysis – The Lur'e problem
 An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e.
Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.
The linear part can be characterized by four matrices (''A'',''B'',''C'',''D''), while the nonlinear part is Φ(''y'') with
An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e.
Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.
The linear part can be characterized by four matrices (''A'',''B'',''C'',''D''), while the nonlinear part is Φ(''y'') with