Non-linear Control on:
[Wikipedia]
[Google]
[Amazon]
Nonlinear control theory is the area of
 An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e.
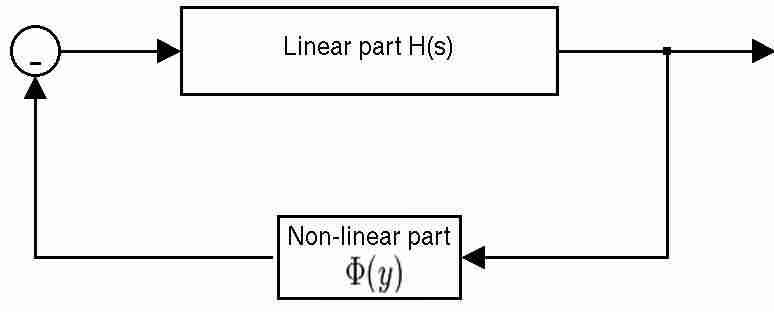
Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.
The linear part can be characterized by four matrices (''A'',''B'',''C'',''D''), while the nonlinear part is Φ(''y'') with
An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e.
Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.
The linear part can be characterized by four matrices (''A'',''B'',''C'',''D''), while the nonlinear part is Φ(''y'') with
control theory
Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a ...
which deals with systems that are nonlinear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...
, time-variant
A time-variant system is a system whose output response depends on moment of observation as well as moment of input signal application. In other words, a time delay or time advance of input not only shifts the output signal in time but also change ...
, or both. Control theory is an interdisciplinary branch of engineering and mathematics that is concerned with the behavior of dynamical system
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water i ...
s with inputs, and how to modify the output by changes in the input using feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled ...
, feedforward
Feedforward is the provision of context of what one wants to communicate prior to that communication. In purposeful activity, feedforward creates an expectation which the actor anticipates. When expected experience occurs, this provides confirmato ...
, or signal filtering. The system to be controlled is called the "plant
Plants are predominantly Photosynthesis, photosynthetic eukaryotes of the Kingdom (biology), kingdom Plantae. Historically, the plant kingdom encompassed all living things that were not animals, and included algae and fungi; however, all curr ...
". One way to make the output of a system follow a desired reference signal is to compare the output of the plant to the desired output, and provide feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled ...
to the plant to modify the output to bring it closer to the desired output.
Control theory is divided into two branches. Linear control theory
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial co ...
applies to systems made of devices which obey the superposition principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So th ...
. They are governed by linear
Linearity is the property of a mathematical relationship ('' function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear ...
differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, a ...
s. A major subclass is systems which in addition have parameters which do not change with time, called ''linear time invariant
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly define ...
'' (LTI) systems. These systems can be solved by powerful frequency domain
In physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency, rather than time. Put simply, a time-domain graph shows how a ...
mathematical techniques of great generality, such as the Laplace transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform that converts a function of a real variable (usually t, in the ''time domain'') to a function of a complex variable s (in the ...
, Fourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, ...
, Z transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain (z-domain or z-plane) representation.
It can be considered as a discrete-time ...
, Bode plot, root locus
In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. This is a technique used as a ...
, and Nyquist stability criterion
In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer at Siemens in 1930 and the Swedish-American electrical engineer Harry ...
.
Nonlinear control theory covers a wider class of systems that do not obey the superposition principle. It applies to more real-world systems, because all real control systems are nonlinear. These systems are often governed by nonlinear differential equation
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many oth ...
s. The mathematical techniques which have been developed to handle them are more rigorous and much less general, often applying only to narrow categories of systems. These include limit cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinit ...
theory, Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower-dimensional ...
s, Lyapunov stability theory, and describing function In control systems theory, the describing function (DF) method, developed by Nikolay Mitrofanovich Krylov and Nikolay Bogoliubov in the 1930s, and extended by Ralph Kochenburger is an approximate procedure for analyzing certain nonlinear contr ...
s. If only solutions near a stable point are of interest, nonlinear systems can often be linearized by approximating them by a linear system obtained by expanding the nonlinear solution in a series
Series may refer to:
People with the name
* Caroline Series (born 1951), English mathematician, daughter of George Series
* George Series (1920–1995), English physicist
Arts, entertainment, and media
Music
* Series, the ordered sets used i ...
, and then linear techniques can be used. Nonlinear systems are often analyzed using numerical method
In numerical analysis, a numerical method is a mathematical tool designed to solve numerical problems. The implementation of a numerical method with an appropriate convergence check in a programming language is called a numerical algorithm.
Mathem ...
s on computers, for example by simulating
A simulation is the imitation of the operation of a real-world process or system over time. Simulations require the use of models; the model represents the key characteristics or behaviors of the selected system or process, whereas the s ...
their operation using a simulation language
A computer simulation language is used to describe the operation of a simulation on a computer.Fritzson, Peter, and Vadim Engelson.Modelica—A unified object-oriented language for system modeling and simulation" European Conference on Object-Orie ...
. Even if the plant is linear, a nonlinear controller can often have attractive features such as simpler implementation, faster speed, more accuracy, or reduced control energy, which justify the more difficult design procedure.
An example of a nonlinear control system is a thermostat
A thermostat is a regulating device component which senses the temperature of a physical system and performs actions so that the system's temperature is maintained near a desired setpoint.
Thermostats are used in any device or system tha ...
-controlled heating system. A building heating system such as a furnace has a nonlinear response to changes in temperature; it is either "on" or "off", it does not have the fine control in response to temperature differences that a proportional (linear) device would have. Therefore, the furnace is off until the temperature falls below the "turn on" setpoint of the thermostat, when it turns on. Due to the heat added by the furnace, the temperature increases until it reaches the "turn off" setpoint of the thermostat, which turns the furnace off, and the cycle repeats. This cycling of the temperature about the desired temperature is called a ''limit cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinit ...
'', and is characteristic of nonlinear control systems.
Properties of nonlinear systems
Some properties of nonlinear dynamic systems are * They do not follow the principle of superposition (linearity and homogeneity). * They may have multiple isolated equilibrium points. * They may exhibit properties such aslimit cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinit ...
, bifurcation
Bifurcation or bifurcated may refer to:
Science and technology
* Bifurcation theory, the study of sudden changes in dynamical systems
** Bifurcation, of an incompressible flow, modeled by squeeze mapping the fluid flow
* River bifurcation, the f ...
, chaos
Chaos or CHAOS may refer to:
Arts, entertainment and media Fictional elements
* Chaos (''Kinnikuman'')
* Chaos (''Sailor Moon'')
* Chaos (''Sesame Park'')
* Chaos (''Warhammer'')
* Chaos, in ''Fabula Nova Crystallis Final Fantasy''
* Cha ...
.
* Finite escape time: Solutions of nonlinear systems may not exist for all times.
Analysis and control of nonlinear systems
There are several well-developed techniques for analyzing nonlinear feedback systems: *Describing function In control systems theory, the describing function (DF) method, developed by Nikolay Mitrofanovich Krylov and Nikolay Bogoliubov in the 1930s, and extended by Ralph Kochenburger is an approximate procedure for analyzing certain nonlinear contr ...
method
* Phase plane method
Phase or phases may refer to:
Science
*State of matter, or phase, one of the distinct forms in which matter can exist
*Phase (matter), a region of space throughout which all physical properties are essentially uniform
*Phase space, a mathematica ...
* Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. T ...
analysis
* Singular perturbation method
* The Popov criterion In nonlinear control and stability theory, the Popov criterion is a stability criterion discovered by Vasile M. Popov for the absolute stability of a class of nonlinear systems whose nonlinearity must satisfy an open-sector condition. While the circ ...
and the circle criterion In nonlinear control and stability theory, the circle criterion is a stability criterion for nonlinear time-varying systems. It can be viewed as a generalization of the Nyquist stability criterion for linear time-invariant (LTI) systems.
Overvi ...
for absolute stability
* Center manifold theorem
* Small-gain theorem
In nonlinear systems
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathema ...
* Passivity analysis
Passive may refer to:
* Passive voice, a grammatical voice common in many languages, see also Pseudopassive
* Passive language, a language from which an interpreter works
* Passivity (behavior), the condition of submitting to the influence of ...
Control design techniques for nonlinear systems also exist. These can be subdivided into techniques which attempt to treat the system as a linear system in a limited range of operation and use (well-known) linear design techniques for each region:
* Gain scheduling
In control theory, gain scheduling is an approach to control of non-linear systems that uses a family of linear controllers, each of which provides satisfactory control for a different operating point of the system.
One or more observable varia ...
Those that attempt to introduce auxiliary nonlinear feedback in such a way that the system can be treated as linear for purposes of control design:
* Feedback linearization
Feedback linearization is a common strategy employed in nonlinear control to control nonlinear systems. Feedback linearization techniques may be applied to nonlinear control systems of the form
where x(t) \in \mathbb^n is the state, u_1(t), ...
And Lyapunov based methods:
* Lyapunov redesign In nonlinear control
Nonlinear control theory is the area of control theory which deals with systems that are nonlinear, time-variant, or both. Control theory is an interdisciplinary branch of engineering and mathematics that is concerned wit ...
* Control-Lyapunov function In control theory, a control-Lyapunov function (CLF) is an extension of the idea of Lyapunov function V(x) to systems with control inputs. The ordinary Lyapunov function is used to test whether a dynamical system is ''(Lyapunov) stable'' or (more ...
* Nonlinear damping
* Backstepping
In control theory, backstepping is a technique developed circa 1990 by Petar V. Kokotovic and others for designing stabilizing controls for a special class of nonlinear dynamical systems. These systems are built from subsystems that radiate out f ...
* Sliding mode control
In control systems, sliding mode control (SMC) is a nonlinear control method that alters the dynamics of a nonlinear system by applying a discontinuous control signal (or more rigorously, a set-valued control signal) that forces the system to "s ...
Nonlinear feedback analysis – The Lur'e problem
 An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e.
Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.
The linear part can be characterized by four matrices (''A'',''B'',''C'',''D''), while the nonlinear part is Φ(''y'') with
An early nonlinear feedback system analysis problem was formulated by A. I. Lur'e.
Control systems described by the Lur'e problem have a forward path that is linear and time-invariant, and a feedback path that contains a memory-less, possibly time-varying, static nonlinearity.
The linear part can be characterized by four matrices (''A'',''B'',''C'',''D''), while the nonlinear part is Φ(''y'') with