neutron magnetic moment on:
[Wikipedia]
[Google]
[Amazon]
The nucleon magnetic moments are the intrinsic magnetic dipole moments of the
 The CODATA recommended value for the magnetic moment of the proton is ''μ''p = = The best available measurement for the value of the magnetic moment of the neutron is Here, ''μ''N is the nuclear magneton, a standard unit for the magnetic moments of nuclear components, and ''μ''B is the Bohr magneton, both being physical constants. In SI units, these values are and A magnetic moment is a vector quantity, and the direction of the nucleon's magnetic moment is determined by its spin. The torque on the neutron that results from an external
The CODATA recommended value for the magnetic moment of the proton is ''μ''p = = The best available measurement for the value of the magnetic moment of the neutron is Here, ''μ''N is the nuclear magneton, a standard unit for the magnetic moments of nuclear components, and ''μ''B is the Bohr magneton, both being physical constants. In SI units, these values are and A magnetic moment is a vector quantity, and the direction of the nucleon's magnetic moment is determined by its spin. The torque on the neutron that results from an external
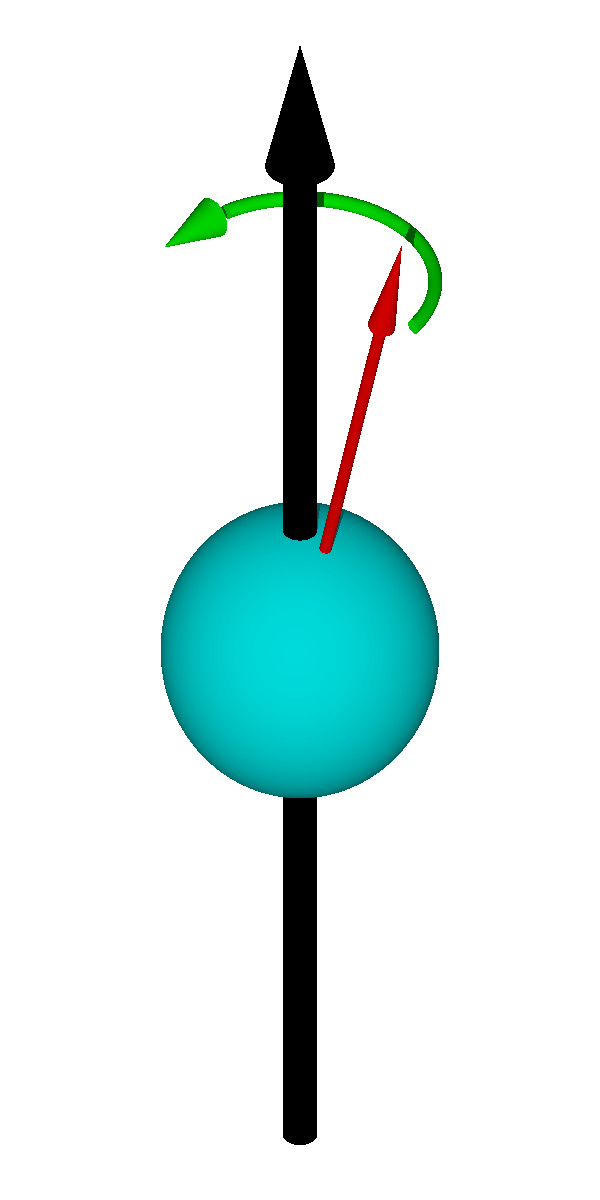
 A magnetic dipole moment can be generated by two possible mechanisms. One way is by a small loop of electric current, called an "Ampèrian" magnetic dipole. Another way is by a pair of magnetic monopoles of opposite magnetic charge, bound together in some way, called a "Gilbertian" magnetic dipole. Elementary magnetic monopoles remain hypothetical and unobserved, however. Throughout the 1930s and 1940s it was not readily apparent which of these two mechanisms caused the nucleon intrinsic magnetic moments. In 1930, Enrico Fermi showed that the magnetic moments of nuclei (including the proton) are Ampèrian.
The two kinds of magnetic moments experience different forces in a magnetic field. Based on Fermi's arguments, the intrinsic magnetic moments of elementary particles, including the nucleons, have been shown to be Ampèrian. The arguments are based on basic electromagnetism, elementary
A magnetic dipole moment can be generated by two possible mechanisms. One way is by a small loop of electric current, called an "Ampèrian" magnetic dipole. Another way is by a pair of magnetic monopoles of opposite magnetic charge, bound together in some way, called a "Gilbertian" magnetic dipole. Elementary magnetic monopoles remain hypothetical and unobserved, however. Throughout the 1930s and 1940s it was not readily apparent which of these two mechanisms caused the nucleon intrinsic magnetic moments. In 1930, Enrico Fermi showed that the magnetic moments of nuclei (including the proton) are Ampèrian.
The two kinds of magnetic moments experience different forces in a magnetic field. Based on Fermi's arguments, the intrinsic magnetic moments of elementary particles, including the nucleons, have been shown to be Ampèrian. The arguments are based on basic electromagnetism, elementary
proton
A proton is a stable subatomic particle, symbol , Hydron (chemistry), H+, or 1H+ with a positive electric charge of +1 ''e'' (elementary charge). Its mass is slightly less than the mass of a neutron and approximately times the mass of an e ...
and neutron
The neutron is a subatomic particle, symbol or , that has no electric charge, and a mass slightly greater than that of a proton. The Discovery of the neutron, neutron was discovered by James Chadwick in 1932, leading to the discovery of nucle ...
, symbols ''μ''p and ''μ''n. The nucleus of an atom
Atoms are the basic particles of the chemical elements. An atom consists of a atomic nucleus, nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished fr ...
comprises protons and neutrons, both nucleons that behave as small magnets. Their magnetic strengths are measured by their magnetic moments. The nucleons interact with normal matter through either the nuclear force or their magnetic moments, with the charged proton also interacting by the Coulomb force.
The proton's magnetic moment was directly measured in 1933 by Otto Stern team in University of Hamburg
The University of Hamburg (, also referred to as UHH) is a public university, public research university in Hamburg, Germany. It was founded on 28 March 1919 by combining the previous General Lecture System ('':de:Allgemeines Vorlesungswesen, ...
. While the neutron was determined to have a magnetic moment by indirect methods in the mid-1930s, Luis Alvarez and Felix Bloch
Felix Bloch (; ; 23 October 1905 – 10 September 1983) was a Swiss-American physicist who shared the 1952 Nobel Prize in Physics with Edward Mills Purcell "for their development of new methods for nuclear magnetic precision measurements and di ...
made the first accurate, direct measurement of the neutron's magnetic moment in 1940. The proton's magnetic moment is exploited to make measurements of molecules by proton nuclear magnetic resonance. The neutron's magnetic moment is exploited to probe the atomic structure of materials using scattering methods and to manipulate the properties of neutron beams in particle accelerators.
The existence of the neutron's magnetic moment and the large value for the proton magnetic moment indicate that nucleons are not elementary particle
In particle physics, an elementary particle or fundamental particle is a subatomic particle that is not composed of other particles. The Standard Model presently recognizes seventeen distinct particles—twelve fermions and five bosons. As a c ...
s. For an elementary particle to have an intrinsic magnetic moment, it must have both spin and electric charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and ...
. The nucleons have spin ''ħ''/2, but the neutron has no net charge. Their magnetic moments were puzzling and defied a valid explanation until the quark model
In particle physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks that give rise to the quantum numbers of the hadrons. The quark model underlies "flavor SU(3)", or the Eig ...
for hadron
In particle physics, a hadron is a composite subatomic particle made of two or more quarks held together by the strong nuclear force. Pronounced , the name is derived . They are analogous to molecules, which are held together by the electri ...
particles was developed in the 1960s. The nucleons are composed of three quarks, and the magnetic moments of these elementary particles combine to give the nucleons their magnetic moments.
Description
 The CODATA recommended value for the magnetic moment of the proton is ''μ''p = = The best available measurement for the value of the magnetic moment of the neutron is Here, ''μ''N is the nuclear magneton, a standard unit for the magnetic moments of nuclear components, and ''μ''B is the Bohr magneton, both being physical constants. In SI units, these values are and A magnetic moment is a vector quantity, and the direction of the nucleon's magnetic moment is determined by its spin. The torque on the neutron that results from an external
The CODATA recommended value for the magnetic moment of the proton is ''μ''p = = The best available measurement for the value of the magnetic moment of the neutron is Here, ''μ''N is the nuclear magneton, a standard unit for the magnetic moments of nuclear components, and ''μ''B is the Bohr magneton, both being physical constants. In SI units, these values are and A magnetic moment is a vector quantity, and the direction of the nucleon's magnetic moment is determined by its spin. The torque on the neutron that results from an external magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
is towards aligning the neutron's spin vector opposite to the magnetic field vector.
The nuclear magneton is the spin magnetic moment of a Dirac particle, a charged, spin-1/2 elementary particle, with a proton's mass p, in which anomalous corrections are ignored. The nuclear magneton is
where is the elementary charge
The elementary charge, usually denoted by , is a fundamental physical constant, defined as the electric charge carried by a single proton (+1 ''e'') or, equivalently, the magnitude of the negative electric charge carried by a single electron, ...
, and is the reduced Planck constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a ...
. The magnetic moment of such a particle is parallel to its spin. Since the neutron has no charge, it should have no magnetic moment by the analogous expression. The non-zero magnetic moment of the neutron thus indicates that it is not an elementary particle. The sign of the neutron's magnetic moment is that of a negatively charged particle. Similarly, that the magnetic moment of the proton, is not almost equal to 1 N indicates that it too is not an elementary particle. Protons and neutrons are composed of quarks, and the magnetic moments of the quarks can be used to compute the magnetic moments of the nucleons.
Although the nucleons interact with normal matter through magnetic forces, the magnetic interactions are many orders of magnitude weaker than the nuclear interactions. The influence of the neutron's magnetic moment is therefore only apparent for low energy, or slow, neutrons. Because the value for the magnetic moment is inversely proportional to particle mass, the nuclear magneton is about 1/2000 as large as the Bohr magneton. The magnetic moment of the electron is therefore about 1000 times larger than that of the nucleons.
The magnetic moments of the antiproton and antineutron have the same magnitudes as their antiparticles,
the proton and neutron, but they have opposite sign.
Measurement
Proton
The magnetic moment of the proton was discovered in 1933 by Otto Stern, Otto Robert Frisch and Immanuel Estermann at theUniversity of Hamburg
The University of Hamburg (, also referred to as UHH) is a public university, public research university in Hamburg, Germany. It was founded on 28 March 1919 by combining the previous General Lecture System ('':de:Allgemeines Vorlesungswesen, ...
. The proton's magnetic moment was determined by measuring the deflection of a beam of molecular hydrogen by a magnetic field. Stern won the Nobel Prize in Physics in 1943 for this discovery.
Neutron
The neutron was discovered in 1932, and since it had no charge, it was assumed to have no magnetic moment. Indirect evidence suggested that the neutron had a non-zero value for its magnetic moment, however, until direct measurements of the neutron's magnetic moment in 1940 resolved the issue. Values for the magnetic moment of the neutron were independently determined by R. Bacher at theUniversity of Michigan
The University of Michigan (U-M, U of M, or Michigan) is a public university, public research university in Ann Arbor, Michigan, United States. Founded in 1817, it is the oldest institution of higher education in the state. The University of Mi ...
at Ann Arbor (1933) and I. Y. Tamm and S. A. Altshuler in the Soviet Union
The Union of Soviet Socialist Republics. (USSR), commonly known as the Soviet Union, was a List of former transcontinental countries#Since 1700, transcontinental country that spanned much of Eurasia from 1922 until Dissolution of the Soviet ...
(1934) from studies of the hyperfine structure of atomic spectra. Although Tamm and Altshuler's estimate had the correct sign and order of magnitude (), the result was met with skepticism.
By 1934 groups led by Stern, now at the Carnegie Institute of Technology in Pittsburgh
Pittsburgh ( ) is a city in Allegheny County, Pennsylvania, United States, and its county seat. It is the List of municipalities in Pennsylvania#Municipalities, second-most populous city in Pennsylvania (after Philadelphia) and the List of Un ...
, and I. I. Rabi at Columbia University
Columbia University in the City of New York, commonly referred to as Columbia University, is a Private university, private Ivy League research university in New York City. Established in 1754 as King's College on the grounds of Trinity Churc ...
in New York had independently measured the magnetic moments of the proton and deuteron
Deuterium (hydrogen-2, symbol H or D, also known as heavy hydrogen) is one of two Stable isotope ratio, stable isotopes of hydrogen; the other is protium, or hydrogen-1, H. The deuterium atomic nucleus, nucleus (deuteron) contains one proton and ...
. The measured values for these particles were only in rough agreement between the groups, but the Rabi group confirmed the earlier Stern measurements that the magnetic moment for the proton was unexpectedly large. Since a deuteron is composed of a proton and a neutron with aligned spins, the neutron's magnetic moment could be inferred by subtracting the deuteron and proton magnetic moments. The resulting value was not zero and had a sign opposite to that of the proton. By the late 1930s, accurate values for the magnetic moment of the neutron had been deduced by the Rabi group using measurements employing newly developed nuclear magnetic resonance techniques.
The value for the neutron's magnetic moment was first directly measured by L. Alvarez and F. Bloch at the University of California
The University of California (UC) is a public university, public Land-grant university, land-grant research university, research university system in the U.S. state of California. Headquartered in Oakland, California, Oakland, the system is co ...
at Berkeley in 1940. Using an extension of the magnetic resonance methods developed by Rabi, Alvarez and Bloch determined the magnetic moment of the neutron to be . By directly measuring the magnetic moment of free neutrons, or individual neutrons free of the nucleus, Alvarez and Bloch resolved all doubts and ambiguities about this anomalous property of neutrons.
Unexpected consequences
The large value for the proton's magnetic moment and the inferred negative value for the neutron's magnetic moment were unexpected and could not be explained. The unexpected values for the magnetic moments of the nucleons would remain a puzzle until thequark model
In particle physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks that give rise to the quantum numbers of the hadrons. The quark model underlies "flavor SU(3)", or the Eig ...
was developed in the 1960s.
The refinement and evolution of the Rabi measurements led to the discovery in 1939 that the deuteron also possessed an electric quadrupole moment. This electrical property of the deuteron had been interfering with the measurements by the Rabi group. The discovery meant that the physical shape of the deuteron was not symmetric, which provided valuable insight into the nature of the nuclear force binding nucleons. Rabi was awarded the Nobel Prize in 1944 for his resonance method for recording the magnetic properties of atomic nuclei.
Nucleon gyromagnetic ratios
The magnetic moment of a nucleon is sometimes expressed in terms of its -factor, a dimensionless scalar. The convention defining the -factor for composite particles, such as the neutron or proton, is where is the intrinsic magnetic moment, is the spinangular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
, and is the effective -factor. While the -factor is dimensionless, for composite particles it is defined relative to the nuclear magneton. For the neutron, is , so the neutron's -factor is while the proton's g-factor is
The gyromagnetic ratio, symbol , of a particle or system is the ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
of its magnetic moment to its spin angular momentum, or
For nucleons, the ratio is conventionally written in terms of the proton mass and charge, by the formula
:
The neutron's gyromagnetic ratio is The proton's gyromagnetic ratio is The gyromagnetic ratio is also the ratio between the observed angular frequency of Larmor precession and the strength of the magnetic field in nuclear magnetic resonance applications, such as in MRI imaging. For this reason, the quantity ''γ''/2''π'' called "gamma bar", expressed in the unit MHz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), often described as being equivalent to one event (or cycle) per second. The hertz is an SI derived unit whose formal expression in terms of SI base u ...
/ T, is often given. The quantities and are therefore convenient.
Physical significance

Larmor precession
When a nucleon is put into a magnetic field produced by an external source, it is subject to a torque tending to orient its magnetic moment parallel to the field (in the case of the neutron, its spin is antiparallel to the field). As with any magnet, this torque is proportional the product of the magnetic moment and the external magnetic field strength. Since the nucleons have spin angular momentum, this torque will cause them to precess with a well-defined frequency, called the Larmor frequency. It is this phenomenon that enables the measurement of nuclear properties through nuclear magnetic resonance. The Larmor frequency can be determined from the product of the gyromagnetic ratio with the magnetic field strength. Since for the neutron the sign of ''γ''n is negative, the neutron's spin angular momentum precesses counterclockwise about the direction of the external magnetic field.Proton nuclear magnetic resonance
Nuclear magnetic resonance employing the magnetic moments of protons is used for nuclear magnetic resonance (NMR) spectroscopy. Since hydrogen-1 nuclei are within themolecules
A molecule is a group of two or more atoms that are held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemistry ...
of many substances, NMR can determine the structure of those molecules.
Determination of neutron spin
The interaction of the neutron's magnetic moment with an external magnetic field was exploited to determine the spin of the neutron. In 1949, D. Hughes and M. Burgy measured neutrons reflected from a ferromagnetic mirror and found that the angular distribution of the reflections was consistent with spin . In 1954, J. Sherwood, T. Stephenson, and S. Bernstein employed neutrons in a Stern–Gerlach experiment that used a magnetic field to separate the neutron spin states. They recorded the two such spin states, consistent with a spin particle. Until these measurements, the possibility that the neutron was a spin particle could not have been ruled out.Neutrons used to probe material properties
Since neutrons are neutral particles, they do not have to overcome Coulomb repulsion as they approach charged targets, unlike protons and alpha particles. Neutrons can deeply penetrate matter. The magnetic moment of the neutron has therefore been exploited to probe the properties of matter usingscattering
In physics, scattering is a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities (including particles and radiat ...
or diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
techniques. These methods provide information that is complementary to X-ray spectroscopy. In particular, the magnetic moment of the neutron is used to determine magnetic properties of materials at length scales of 1–100 Å using cold or thermal neutrons. B. Brockhouse and C. Shull won the Nobel Prize
The Nobel Prizes ( ; ; ) are awards administered by the Nobel Foundation and granted in accordance with the principle of "for the greatest benefit to humankind". The prizes were first awarded in 1901, marking the fifth anniversary of Alfred N ...
in physics in 1994 for developing these scattering techniques.
Control of neutron beams by magnetism
As neutrons carry no electric charge, neutron beams cannot be controlled by the conventional electromagnetic methods employed inparticle accelerators
A particle accelerator is a machine that uses electromagnetic fields to propel electric charge, charged particles to very high speeds and energies to contain them in well-defined particle beam, beams. Small accelerators are used for fundamental ...
. The magnetic moment of the neutron allows some control of neutrons using magnetic fields, however, including the formation of polarized neutron beams. One technique employs the fact that cold neutrons will reflect from some magnetic materials at great efficiency when scattered at small grazing angles. The reflection preferentially selects particular spin states, thus polarizing the neutrons. Neutron magnetic mirrors and guides use this total internal reflection phenomenon to control beams of slow neutrons.
Nuclear magnetic moments
Since an atomic nucleus consists of a bound state of protons and neutrons, the magnetic moments of the nucleons contribute to the nuclear magnetic moment, or the magnetic moment for the nucleus as a whole. The nuclear magnetic moment also includes contributions from the orbital motion of the charged protons. The deuteron, consisting of a proton and a neutron, has the simplest example of a nuclear magnetic moment. The sum of the proton and neutron magnetic moments gives 0.879 ''μ''N, which is within 3% of the measured value 0.857 ''μ''N. In this calculation, the spins of the nucleons are aligned, but their magnetic moments offset because of the neutron's negative magnetic moment.Nature of the nucleon magnetic moments
 A magnetic dipole moment can be generated by two possible mechanisms. One way is by a small loop of electric current, called an "Ampèrian" magnetic dipole. Another way is by a pair of magnetic monopoles of opposite magnetic charge, bound together in some way, called a "Gilbertian" magnetic dipole. Elementary magnetic monopoles remain hypothetical and unobserved, however. Throughout the 1930s and 1940s it was not readily apparent which of these two mechanisms caused the nucleon intrinsic magnetic moments. In 1930, Enrico Fermi showed that the magnetic moments of nuclei (including the proton) are Ampèrian.
The two kinds of magnetic moments experience different forces in a magnetic field. Based on Fermi's arguments, the intrinsic magnetic moments of elementary particles, including the nucleons, have been shown to be Ampèrian. The arguments are based on basic electromagnetism, elementary
A magnetic dipole moment can be generated by two possible mechanisms. One way is by a small loop of electric current, called an "Ampèrian" magnetic dipole. Another way is by a pair of magnetic monopoles of opposite magnetic charge, bound together in some way, called a "Gilbertian" magnetic dipole. Elementary magnetic monopoles remain hypothetical and unobserved, however. Throughout the 1930s and 1940s it was not readily apparent which of these two mechanisms caused the nucleon intrinsic magnetic moments. In 1930, Enrico Fermi showed that the magnetic moments of nuclei (including the proton) are Ampèrian.
The two kinds of magnetic moments experience different forces in a magnetic field. Based on Fermi's arguments, the intrinsic magnetic moments of elementary particles, including the nucleons, have been shown to be Ampèrian. The arguments are based on basic electromagnetism, elementary quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, and the hyperfine structure of atomic s-state energy levels. In the case of the neutron, the theoretical possibilities were resolved by laboratory measurements of the scattering of slow neutrons from ferromagnetic materials in 1951.
Anomalous magnetic moments and meson physics
The anomalous values for the magnetic moments of the nucleons presented a theoretical quandary for the 30 years from the time of their discovery in the early 1930s to the development of the quark model in the 1960s. Considerable theoretical efforts were expended in trying to understand the origins of these magnetic moments, but the failures of these theories were glaring. Much of the theoretical focus was on developing a nuclear-force equivalence to the remarkably successful theory explaining the small anomalous magnetic moment of the electron. The problem of the origins of the magnetic moments of nucleons was recognized as early as 1935. G. C. Wick suggested that the magnetic moments could be caused by the quantum-mechanical fluctuations of these particles in accordance with Fermi's 1934 theory of beta decay. By this theory, a neutron is partly, regularly and briefly, disassociated into a proton, an electron, and a neutrino as a natural consequence ofbeta decay
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which an atomic nucleus emits a beta particle (fast energetic electron or positron), transforming into an isobar of that nuclide. For example, beta decay of a neutron ...
. By this idea, the magnetic moment of the neutron was caused by the fleeting existence of the large magnetic moment of the electron in the course of these quantum-mechanical fluctuations, the value of the magnetic moment determined by the length of time the virtual electron was in existence. The theory proved to be untenable, however, when H. Bethe and R. Bacher showed that it predicted values for the magnetic moment that were either much too small or much too large, depending on speculative assumptions.
Similar considerations for the electron proved to be much more successful. In quantum electrodynamics
In particle physics, quantum electrodynamics (QED) is the Theory of relativity, relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quant ...
(QED), the anomalous magnetic moment of a particle stems from the small contributions of quantum mechanical fluctuations to the magnetic moment
In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude ...
of that particle.
The g-factor for a "Dirac" magnetic moment
In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude ...
is predicted to be for a negatively charged, spin-1/2 particle. For particles such as the electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
, this "classical" result differs from the observed value by around 0.1%; the difference compared to the classical value is the anomalous magnetic moment. The ''g''-factor for the electron is measured to be QED is the theory of the mediation of the electromagnetic force by photons. The physical picture is that the ''effective'' magnetic moment of the electron results from the contributions of the "bare" electron, which is the Dirac particle, and the cloud of "virtual", short-lived electron–positron pairs and photons that surround this particle as a consequence of QED. The effects of these quantum mechanical fluctuations can be computed theoretically using Feynman diagrams with loops.
The one-loop contribution to the anomalous magnetic moment of the electron, corresponding to the first-order and largest correction in QED, is found by calculating the vertex function shown in the diagram on the right. The calculation was discovered by J. Schwinger in 1948. Computed to fourth order, the QED prediction for the electron's anomalous magnetic moment agrees with the experimentally measured value to more than 10 significant figures, making the magnetic moment of the electron one of the most accurately verified predictions in the history of physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
.
Compared to the electron, the anomalous magnetic moments of the nucleons are enormous. The g-factor for the proton is 5.6, and the chargeless neutron, which should have no magnetic moment at all, has a g-factor of −3.8. Note, however, that the anomalous magnetic moments of the nucleons, that is, their magnetic moments with the expected Dirac particle magnetic moments subtracted, are roughly equal but of opposite sign: , but .
The Yukawa interaction for nucleons was discovered in the mid-1930s, and this nuclear force is mediated by pion
In particle physics, a pion (, ) or pi meson, denoted with the Greek alphabet, Greek letter pi (letter), pi (), is any of three subatomic particles: , , and . Each pion consists of a quark and an antiquark and is therefore a meson. Pions are the ...
meson
In particle physics, a meson () is a type of hadronic subatomic particle composed of an equal number of quarks and antiquarks, usually one of each, bound together by the strong interaction. Because mesons are composed of quark subparticles, the ...
s. In parallel with the theory for the electron, the hypothesis was that higher-order loops involving nucleons and pions may generate the anomalous magnetic moments of the nucleons. The physical picture was that the ''effective'' magnetic moment of the neutron arose from the combined contributions of the "bare" neutron, which is zero, and the cloud of "virtual" pions and photons that surround this particle as a consequence of the nuclear and electromagnetic forces. The Feynman diagram at right is roughly the first-order diagram, with the role of the virtual particles played by pions. As noted by A. Pais, "between late 1948 and the middle of 1949 at least six papers appeared reporting on second-order calculations of nucleon moments". These theories were also, as noted by Pais, "a flop" they gave results that grossly disagreed with observation. Nevertheless, serious efforts continued along these lines for the next couple of decades, to little success.
These theoretical approaches were incorrect because the nucleons are composite particles with their magnetic moments arising from their elementary components, quarks.
Quark model of nucleon magnetic moments
In thequark model
In particle physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks that give rise to the quantum numbers of the hadrons. The quark model underlies "flavor SU(3)", or the Eig ...
for hadrons, the neutron is composed of one up quark (charge ) and two down quarks (charge ) while the proton is composed of one down quark (charge ) and two up quarks (charge ).
The magnetic moment of the nucleons can be modeled as a sum of the magnetic moments of the constituent quarks, although this simple model belies the complexities of the Standard Model of Particle Physics.
The calculation assumes that the quarks behave like pointlike Dirac particles, each having their own magnetic moment, as computed using an expression similar to the one above for the nuclear magneton:
where the q-subscripted variables refer to quark magnetic moment, charge, or mass. Simplistically, the magnetic moment of a nucleon can be viewed as resulting from the vector sum of the three quark magnetic moments, plus the orbital magnetic moments caused by the movement of the three charged quarks within it.
In one of the early successes of the Standard Model (SU(6) theory), in 1964 M. Beg, B. Lee, and A. Pais theoretically calculated the ratio of proton-to-neutron magnetic moments to be , which agrees with the experimental value to within 3%.
The measured value for this ratio is . The database was developed by J. Baker, M. Douma, and S. Kotochigova. A contradiction of the quantum mechanical basis of this calculation with the Pauli exclusion principle led to the discovery of the color charge for quarks by O. Greenberg in 1964.
From the nonrelativistic quantum-mechanical wave function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
for baryon
In particle physics, a baryon is a type of composite particle, composite subatomic particle that contains an odd number of valence quarks, conventionally three. proton, Protons and neutron, neutrons are examples of baryons; because baryons are ...
s composed of three quarks, a straightforward calculation gives fairly accurate estimates for the magnetic moments of neutrons, protons, and other baryons. For a neutron, the magnetic moment is given by where d and u are the magnetic moments for the down and up quarks respectively. This result combines the intrinsic magnetic moments of the quarks with their orbital magnetic moments and assumes that the three quarks are in a particular, dominant quantum state.
The results of this calculation are encouraging, but the masses of the up or down quarks were assumed to be the mass of a nucleon. The masses of the quarks are actually only about 1% that of a nucleon. The discrepancy stems from the complexity of the Standard Model for nucleons, where most of their mass originates in the gluon
A gluon ( ) is a type of Massless particle, massless elementary particle that mediates the strong interaction between quarks, acting as the exchange particle for the interaction. Gluons are massless vector bosons, thereby having a Spin (physi ...
fields, virtual particles, and their associated energy that are essential aspects of the strong force.
Furthermore, the complex system of quarks and gluons that constitute a nucleon requires a relativistic treatment.
Nucleon magnetic moments have been successfully computed from first principle
In philosophy and science, a first principle is a basic proposition or assumption that cannot be deduced from any other proposition or assumption. First principles in philosophy are from first cause attitudes and taught by Aristotelians, and nuan ...
s, requiring significant computing resources.
See also
* Aharonov–Casher effect * LARMOR neutron microscope * Neutron electric dipole moment * Neutron triple-axis spectrometryReferences
Bibliography
* S. W. Lovesey (1986). Theory of Neutron Scattering from Condensed Matter. Oxford University Press. . * Donald H. Perkins (1982). Introduction to High Energy Physics. Reading, Massachusetts: Addison Wesley, . * John S. Rigden (1987). Rabi, Scientist and Citizen. New York: Basic Books, Inc., . * Sergei Vonsovsky (1975). Magnetism of Elementary Particles. Moscow: Mir Publishers.External links
* {{Commons category-inline Electric and magnetic fields in matter Magnetic moment Magnetism Magnetostaticsmagnetic moment
In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude ...
magnetic moment
In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude ...
Physical quantities