Mādhava's Sine Table

Madhava's sine table is the table of trigonometric sines of various angles constructed by the 14th century Kerala mathematician- astronomer Madhava of Sangamagrama. The table lists the trigonometric sines of the twenty-four angles 3.75°, 7.50°, 11.25°, ..., and 90.00° (angles that are integral multiples of 3.75°, i.e. 1/24 of a right angle, beginning with 3.75 and ending with 90.00). The table is encoded in the letters of Devanagari using the Katapayadi system. This gives the entries in the table an appearance of the verses of a poem in Sanskrit.

Madhava's original work containing the sine table has not yet been traced. The table is seen reproduced in the ''Aryabhatiyabhashya'' of Nilakantha Somayaji''The Aryabhatiam of Aryabhattacharya with the Bhashya of Nilakantha Somasutvan, Part1-Gaṇitapāda,'' Edited by K. Sambasiva Sastri, Trivandrum Sanskrit Series No.101. p. 55.

https://archive.org/details/Trivandrum_Sanskrit_Series_TSS

http://www.sanskritebooks.org/2013/02/trivandrum-sanskrit-series-anantasayana-samskrita-granthavali/(1444–1544) and also in the ''Yuktidipika/Laghuvivrti'' commentary of Tantrasamgraha by Sankara Variar (circa. 1500-1560).

The table

The image below gives Madhava's sine table in Devanagari as reproduced in ''Cultural foundations of mathematics'' by C.K. Raju. The first twelve lines constitute the entries in the table. The last word in the thirteenth line indicates that these are "as told by Madhava".

Values in Madhava's table

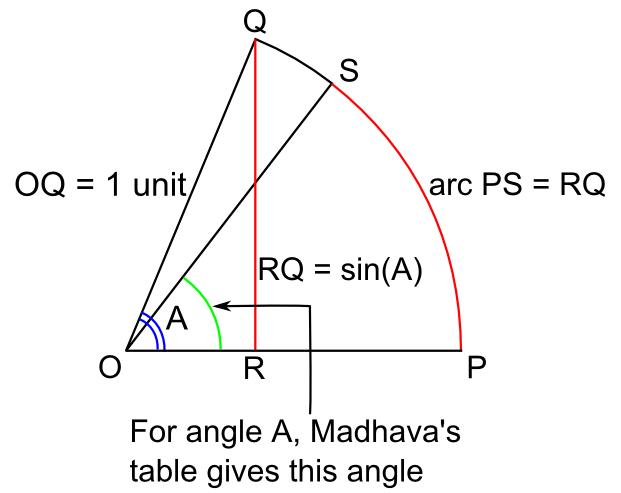
To understand the meaning of the values tabulated by Madhava, consider some angle whose measure is A. Consider a circle of unit radius and center O. Let the arc PQ of the circle subtend an angle A at the center O. Drop the perpendicular QR from Q to OP; then the length of the line segment RQ is the value of the trigonometric sine of the angle A. Let PS be an arc of the circle whose length is equal to the length of the segment RQ. For various angles A, Madhava's table gives the measures of the corresponding angles $\angle$POS in arcminutes, arcseconds and sixtieths of an arcsecond.

As an example, let A be an angle whose measure is 22.50°. In Madhava's table, the entry corresponding to 22.50° is the measure in arcminutes, arcseconds and sixtieths of arcseconds of the angle whose radian measure is the modern value of sin 22.50°. The modern numerical value of sin 22.50° is 0.382683432363 and,

:0.382683432363 radians = 180 / π × 0.382683432363 degrees = 21.926145564094 degrees.

and

:21.926145564094 degrees = 1315 arcminutes 34 arcseconds 07 sixtieths of arcsecond.

In the Katapayadi system the digits are written in the reverse order. Thus in Madhava's table, the entry corresponding to 22.50° is 70435131.

Derivation of trigonometric sines from Madhava's table

For an angle whose measure is ''A'', let

:$\angle POS = m \text s \text t \text$

Then

:$\begin \sin (A) & = RQ \\ & = \text PS \\ & = \angle POS \text\\ & = \frac\left( m + \frac+ \frac\right). \end$

Each of the lines in the table specifies eight digits. Let the digits corresponding to angle A (read from left to right) be

:$d_1\quad d_2\quad d_3\quad d_4\quad d_5\quad d_6\quad d_7\quad d_8$

Then according to the rules of the Katapayadi system of Kerala mathematicians we have

:$\begin m & = d_8\times 1000 + d_7\times 100 + d_6 \times 10 +d_5\\ s & = d_4\times 10 + d_3\\ t & = d_2\times 10 + d_1 \end$

Madhava's value of pi

To complete the numerical computations one must have a knowledge of the value of pi ($\pi$). It is appropriate that we use the value of π computed by Madhava himself. Nilakantha Somayaji has given this value of π in his Āryabhaṭīya-Bhashya as follows:

A transliteration of the last two lines:

vibudha-netra-gaja-ahi-hutāśana
tri-guṇa-veda-bha-vāraṇa-bāhavaḥ
nava-nikharva-mite vr̥tivistare
paridhi-mānam idaṁ jagadur budhāḥ

The various words indicate certain numbers encoded in a scheme known as the bhūtasaṃkhyā system. The meaning of the words and the numbers encoded by them (beginning with the units place) are detailed in the following translation of the verse:
"Gods (vibudha : 33), eyes (netra : 2), elephants (gaja : 8), snakes (ahi : 8), fires (hutāśana : 3), three (tri : 3), qualities (guṇa : 3), vedas (veda : 4), nakṣatras (bha : 27), elephants (vāraṇa : 8), and arms (bāhavaḥ : 2) - the wise say that this is the measure of the circumference when the diameter of a circle is nava-nikharva (900,000,000,000)."

So, the translation of the poem using the bhūtasaṃkhyā system will simply read "2827433388233 is, as the wise say, the circumference of a circle whose diameter is nava-nikharva (900,000,000,000)". That is, divide 2827433388233 (the number from the first two lines of the poem in reverse order) by nava-nikharva (900,000,000,000) to get the value of pi (π). This calculation yields the value π = 3.1415926535922. This is the value of π used by Madhava in his further calculations and is accurate to 11 decimal places.

Example

Madhava's table lists the following digits corresponding to the angle 45.00°:

:$5\quad 1\quad 1\quad 5\quad 0\quad 3\quad 4\quad 2$

This yields the angle with measure

:$\begin m & = 2\times 1000 + 4\times 100 + 3\times 10 + 0 \text\\ & = 2430 \text \\ s & = 5\times 10 + 1 \text\\ & = 51 \text\\ t & = 1\times 10 + 5 \text\\ & = 15 \text \end$
The value of the trigonometric sine of 45.00° as given in Madhava's table is

:$\sin 45^\circ = \frac\left( 2430 + \frac + \frac\right)$

Substituting the value of π computed by Madhava in the above expression, one gets sin 45° as 0.70710681.

This value may be compared with the modern exact value of sin 45.00°, namely, 0.70710678.

Comparison of Madhava's and modern sine values

In table below the first column contains the list of the twenty-four angles beginning with 3.75 and ending with 90.00. The second column contains the values tabulated by Madhava in Devanagari in the form in which it was given by Madhava. (These are taken from ''Malayalam Commentary of Karanapaddhati'' by P.K. Koru (Published in 1953) and are slightly different from the table given in ''Cultural foundations of mathematics'' by C.K. Raju.) The third column contains ISO 15919 transliterations of the lines given in the second column. The digits encoded by the lines in second column are given in Arabic numerals in the fourth column. The values of the trigonometric sines derived from the numbers specified in Madhava's table are listed in the fifth column. These values are computed using the approximate value 3.1415926535922 for π obtained by Madhava. For comparison, the exact values of the trigonometric sines of the angles are given in the sixth column.

Madhava's method of computation

No work of Madhava detailing the methods used by him for the computation of the sine table has survived. However from the writings of later Kerala mathematicians like Nilakantha Somayaji ( Tantrasangraha) and Jyeshtadeva (Yuktibhāṣā) that give ample references to Madhava's accomplishments, it is conjectured that Madhava computed his sine table using the power series expansion of sin ''x''.

:$\sin x = x - \frac + \frac - \frac + \cdots$

See also

*Madhava series
* Āryabhaṭa's sine table
* Ptolemy's table of chords

References

Further references

*
*For an account of Madhava's computation of the sine table see :
*For a thorough discussion of the computation of Madhava's sine table with historical references :

{{DEFAULTSORT:Madhava's Sine Table
Trigonometry
Indian mathematics
Kerala school of astronomy and mathematics