Movable cellular automaton on:
[Wikipedia]
[Google]
[Amazon]
The movable cellular automaton (MCA) method is a method in computational solid mechanics based on the discrete concept. It provides advantages both of classical cellular automaton and discrete element methods. One important advantage of the MCA method is that it permits direct
 In framework of the MCA approach an object under modeling is considered as a set of interacting elements/automata. The dynamics of the set of automata are defined by their mutual forces and rules for their relationships. This system exists and operates in time and space. Its evolution in time and space is governed by the equations of motion. The mutual forces and rules for inter-elements relationships are defined by the function of the automaton response. This function has to be specified for each automaton. Due to mobility of automata the following new parameters of cellular automata have to be included into consideration: ''Ri'' – radius-vector of automaton; ''Vi'' – velocity of automaton; ωi – rotation velocity of automaton; ''θi'' – rotation vector of automaton; ''mi'' – mass of automaton; ''Ji'' – moment of inertia of automaton.
In framework of the MCA approach an object under modeling is considered as a set of interacting elements/automata. The dynamics of the set of automata are defined by their mutual forces and rules for their relationships. This system exists and operates in time and space. Its evolution in time and space is governed by the equations of motion. The mutual forces and rules for inter-elements relationships are defined by the function of the automaton response. This function has to be specified for each automaton. Due to mobility of automata the following new parameters of cellular automata have to be included into consideration: ''Ri'' – radius-vector of automaton; ''Vi'' – velocity of automaton; ωi – rotation velocity of automaton; ''θi'' – rotation vector of automaton; ''mi'' – mass of automaton; ''Ji'' – moment of inertia of automaton.
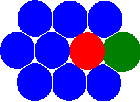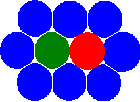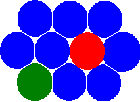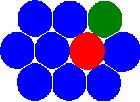 The new concept of the MCA method is based on the introducing of the state of the pair of automata (relation of interacting pairs of automata) in addition to the conventional one – the state of a separate automaton. Note that the introduction of this definition allows to go from the static net concept to the concept of neighbours. As a result of this, the automata have the ability to change their neighbors by switching the states (relationships) of the pairs.
The new concept of the MCA method is based on the introducing of the state of the pair of automata (relation of interacting pairs of automata) in addition to the conventional one – the state of a separate automaton. Note that the introduction of this definition allows to go from the static net concept to the concept of neighbours. As a result of this, the automata have the ability to change their neighbors by switching the states (relationships) of the pairs.
MCA software package
* Software for simulation of materials in discrete-continuous approach «FEM+MCA»: Number of state registration in Applied Research Foundation of Algorithms and Software (AFAS): 50208802297 / Smolin A.Y., Zelepugin S.A., Dobrynin S.A.; applicant and development center is Tomsk State University. – register date 28.11.2008
certificate AFAS N 11826 date 01.12.2008.
Solid mechanics Numerical analysis Cellular automata Condensed matter physics Mathematical modeling
simulation
A simulation is the imitation of the operation of a real-world process or system over time. Simulations require the use of Conceptual model, models; the model represents the key characteristics or behaviors of the selected system or proc ...
of material fracture, including damage generation, crack propagation, fragmentation, and mass mixing. It is difficult to simulate these processes by means of continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such m ...
methods (For example: finite element method, finite difference method, etc.), so some new concepts like peridynamics
Peridynamics is a formulation of continuum mechanics that is oriented toward deformations with discontinuities, especially fractures.
Purpose
The peridynamic theory is based on integral equations, in contrast with the classical theory of contin ...
are required. Discrete element method
A discrete element method (DEM), also called a distinct element method, is any of a family of numerical methods for computing the motion and effect of a large number of small particles. Though DEM is very closely related to molecular dynamics, t ...
is very effective to simulate granular materials, but mutual forces among movable cellular automata provides simulating solids behavior. As the cell size of the automaton approaches zero, MCA behavior approaches classical continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such m ...
methods. The MCA method was developed in the group of S.G. Psakhie
Keystone of the movable cellular automaton method
 In framework of the MCA approach an object under modeling is considered as a set of interacting elements/automata. The dynamics of the set of automata are defined by their mutual forces and rules for their relationships. This system exists and operates in time and space. Its evolution in time and space is governed by the equations of motion. The mutual forces and rules for inter-elements relationships are defined by the function of the automaton response. This function has to be specified for each automaton. Due to mobility of automata the following new parameters of cellular automata have to be included into consideration: ''Ri'' – radius-vector of automaton; ''Vi'' – velocity of automaton; ωi – rotation velocity of automaton; ''θi'' – rotation vector of automaton; ''mi'' – mass of automaton; ''Ji'' – moment of inertia of automaton.
In framework of the MCA approach an object under modeling is considered as a set of interacting elements/automata. The dynamics of the set of automata are defined by their mutual forces and rules for their relationships. This system exists and operates in time and space. Its evolution in time and space is governed by the equations of motion. The mutual forces and rules for inter-elements relationships are defined by the function of the automaton response. This function has to be specified for each automaton. Due to mobility of automata the following new parameters of cellular automata have to be included into consideration: ''Ri'' – radius-vector of automaton; ''Vi'' – velocity of automaton; ωi – rotation velocity of automaton; ''θi'' – rotation vector of automaton; ''mi'' – mass of automaton; ''Ji'' – moment of inertia of automaton.
New concept: neighbours
 The new concept of the MCA method is based on the introducing of the state of the pair of automata (relation of interacting pairs of automata) in addition to the conventional one – the state of a separate automaton. Note that the introduction of this definition allows to go from the static net concept to the concept of neighbours. As a result of this, the automata have the ability to change their neighbors by switching the states (relationships) of the pairs.
The new concept of the MCA method is based on the introducing of the state of the pair of automata (relation of interacting pairs of automata) in addition to the conventional one – the state of a separate automaton. Note that the introduction of this definition allows to go from the static net concept to the concept of neighbours. As a result of this, the automata have the ability to change their neighbors by switching the states (relationships) of the pairs.
Definition of the parameter of pair state
The introducing of new type of states leads to new parameter to use it as criteria for switching relationships. It is defined as an automaton overlapping parameters ''hij''. So the relationship of the cellular automata is characterised by the value of their overlapping. The initial structure is formed by setting up certain relationships among each pair of neighboring elements.Criterion of switching of the state of pair relationships
In contrast to the classical cellular automaton method in the MCA method not only a single automaton but also a relationship of pair of automata can be switched. According with the bistable automata concept there are two types of the pair states (relationships): So the changing of the state of pair relationships is controlled by relative movements of the automata and the media formed by such pairs can be considered as bistable media.Equations of MCA motion
The evolution of MCA media is described by the following equations of motion for translation: : Here is the mass of automaton , is central force acting between automata and , is certain coefficient associated with transferring the h parameter from pair ij to pair ik, is the angle between directions ij and ik. Due to finite size of movable automata the rotation effects have to be taken into account. The equations of motion for rotation can be written as follows: : Here Θij is the angle of relative rotation (it is a switching parameter like hij for translation), qij is the distance from center of automaton i to contact point of automaton j (moment arm), τij is the pair tangential interaction, is certain coefficient associated with transferring the Θ parameter from one pair to other (it is similar to from the equation for translation). These equations are completely similar to the equations of motion for the many–particle approach.Definition of deformation in pair of automata
Translation of the pair automata The dimensionless deformation parameter for translation of the i j automata pair can be presented as: : In this case: : where Δt time step, Vnij – relative velocity. Rotation of the pair automata can be calculated by analogy with the last translation relationships.Modeling of irreversible deformation in the MCA method
The εij parameter is used as a measure of deformation of automaton i under its interaction with automaton j. Where qij – is a distance from the center of automaton i to its contact point with automaton j; Ri = di/2 (di – is the size of automaton i). As an example the titanium specimen under cyclic loading (tension – compression) is considered. The loading diagram is shown in the next figure:Advantages of MCA method
Due to mobility of each automaton the MCA method allows to take into account directly such actions as: * mass mixing * penetration effects * chemical reactions * intensive deformation * phase transformations * accumulation of damages * fragmentation and fracture * cracks generation and development Using boundary conditions of different types (fixed, elastic, viscous-elastic, etc.) it is possible to imitate different properties of surrounding medium, containing the simulated system. It is possible to model different modes of mechanical loading (tension, compression, shear strain, etc.) by setting up additional conditions at the boundaries.See also
* * * * * * * * *References
* * () * () * * * * * * () * * * () * ({{cite book, last=Добрынин, first=Сергей, title=Компьютерное моделирование методом подвижных клеточных автоматов, publisher=LAP LAMBERT Academic Publishing, year=2011, location=Saarbrücken Germany, page=132, url=https://www.lap-publishing.com/catalog/details/store/gb/book/978-3-8443-5954-1/%D0%9A%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80%D0%BD%D0%BE%D0%B5-%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5-%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%BE%D0%BC-%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D1%85-%D0%BA%D0%BB%D0%B5%D1%82%D0%BE%D1%87%D0%BD%D1%8B%D1%85-%D0%B0%D0%B2%D1%82%D0%BE%D0%BC%D0%B0%D1%82%D0%BE%D0%B2, isbn = 978-3-8443-5954-1, access-date = 2011-11-19 , language=ru)Software
MCA software package
* Software for simulation of materials in discrete-continuous approach «FEM+MCA»: Number of state registration in Applied Research Foundation of Algorithms and Software (AFAS): 50208802297 / Smolin A.Y., Zelepugin S.A., Dobrynin S.A.; applicant and development center is Tomsk State University. – register date 28.11.2008
certificate AFAS N 11826 date 01.12.2008.
Solid mechanics Numerical analysis Cellular automata Condensed matter physics Mathematical modeling