Montgomery's pair correlation conjecture on:
[Wikipedia]
[Google]
[Amazon]
 In
In
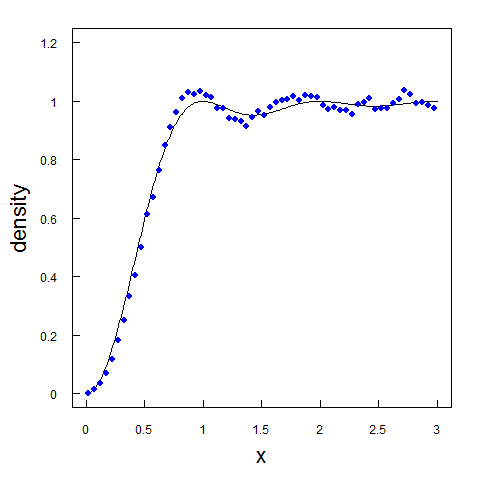 In the 1980s, motivated by Montgomery's conjecture, Odlyzko began an intensive numerical study of the statistics of the zeros of ζ(''s''). He confirmed the distribution of the spacings between non-trivial zeros using detailed numerical calculations and demonstrated that Montgomery's conjecture would be true and that the distribution would agree with the distribution of spacings of GUE random matrix eigenvalues using
In the 1980s, motivated by Montgomery's conjecture, Odlyzko began an intensive numerical study of the statistics of the zeros of ζ(''s''). He confirmed the distribution of the spacings between non-trivial zeros using detailed numerical calculations and demonstrated that Montgomery's conjecture would be true and that the distribution would agree with the distribution of spacings of GUE random matrix eigenvalues using
 In
In mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, Montgomery's pair correlation conjecture is a conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), ha ...
made by that the pair correlation between pairs of zeros of the Riemann zeta function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for and its analytic c ...
(normalized to have unit average spacing) is
:
which, as Freeman Dyson
Freeman John Dyson (15 December 1923 – 28 February 2020) was a British-American theoretical physics, theoretical physicist and mathematician known for his works in quantum field theory, astrophysics, random matrix, random matrices, math ...
pointed out to him, is the same as the pair correlation function of random Hermitian matrices.
Conjecture
''Under the assumption that theRiemann hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pure ...
is true.''
Let be fixed, then the conjecture states
:
and where each is the imaginary part of the non-trivial zeros of Riemann zeta function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for and its analytic c ...
, that is .
Explanation
Informally, this means that the chance of finding a zero in a very short interval of length 2π''L''/log(''T'') at a distance 2π''u''/log(''T'') from a zero 1/2+''iT'' is about ''L'' times the expression above. (The factor 2π/log(''T'') is a normalization factor that can be thought of informally as the average spacing between zeros withimaginary part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
about ''T''.) showed that the conjecture was supported by large-scale computer calculations of the zeros. The conjecture has been extended to correlations of more than two zeros, and also to zeta functions of automorphic representations . In 1982 a student of Montgomery's, Ali Erhan Özlük, proved the pair correlation conjecture for some of Dirichlet's L-functions.
The connection with random unitary matrices could lead to a proof of the Riemann hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pure ...
(RH). The Hilbert–Pólya conjecture
In mathematics, the Hilbert–Pólya conjecture states that the non-trivial Zero of a function, zeros of the Riemann zeta function correspond to eigenvalues of a self-adjoint operator. It is a possible approach to the Riemann hypothesis, by means o ...
asserts that the zeros of the Riemann Zeta function correspond to the eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s of a linear operator
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that pr ...
, and implies RH. Some people think this is a promising approach ().
Montgomery was studying the Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
''F''(''x'') of the pair correlation function, and showed (assuming the Riemann hypothesis) that it was
equal to , ''x'', for , ''x'', < 1. His methods were unable to determine it for , ''x'', ≥ 1, but he conjectured that it was equal to 1 for these ''x'', which implies that the pair correlation function is as above. He was also motivated by the notion that the Riemann hypothesis is not a brick wall, and one should feel free to make ''stronger'' conjectures.
F(α) conjecture or strong pair correlation conjecture
Let again and stand for non-trivial zeros of the Riemann zeta function. Montgomery introduced the function : for and some weight function . Montgomery and Goldston proved under the Riemann hypothesis, that for this function converges uniformly : Montgomery conjectured, which is now known as the ''F(α) conjecture'' or ''strong pair correlation conjecture'', that for we have uniform convergence : for in a bounded interval.Numerical calculation by Odlyzko
 In the 1980s, motivated by Montgomery's conjecture, Odlyzko began an intensive numerical study of the statistics of the zeros of ζ(''s''). He confirmed the distribution of the spacings between non-trivial zeros using detailed numerical calculations and demonstrated that Montgomery's conjecture would be true and that the distribution would agree with the distribution of spacings of GUE random matrix eigenvalues using
In the 1980s, motivated by Montgomery's conjecture, Odlyzko began an intensive numerical study of the statistics of the zeros of ζ(''s''). He confirmed the distribution of the spacings between non-trivial zeros using detailed numerical calculations and demonstrated that Montgomery's conjecture would be true and that the distribution would agree with the distribution of spacings of GUE random matrix eigenvalues using Cray X-MP
The Cray X-MP was a supercomputer designed, built and sold by Cray, Cray Research. It was announced in 1982 as the "cleaned up" successor to the 1975 Cray-1, and was the world's fastest computer from 1983 to 1985 with a quad-processor system perfo ...
. In 1987 he reported the calculations in the paper .
For non-trivial zero, 1/2 + iγ''n'', let the normalized spacings be
:
Then we would expect the following formula as the limit for :
:
Based on a new algorithm developed by Odlyzko and Arnold Schönhage that allowed them to compute a value of ζ(1/2 + i''t'') in an average time of ''t''ε steps, Odlyzko computed millions of zeros at heights around 1020 and gave some evidence for the GUE conjecture.A. M. Odlyzko, "The 1020-th zero of the Riemann zeta function and 70 million of its neighbors," AT&T Bell Lab. preprint (1989)M. Mehta (1990), chap.1
The figure contains the first 105 non-trivial zeros of the Riemann zeta function. As more zeros are sampled, the more closely their distribution approximates the shape of the GUE random matrix.
See also
* Lehmer pairReferences
* * * * *{{Citation , author2-link=Peter Sarnak , last1=Rudnick , first1=Zeév , last2=Sarnak , first2=Peter , title=Zeros of principal L-functions and random matrix theory , doi=10.1215/S0012-7094-96-08115-6 , mr=1395406 , year=1996 , journal=Duke Mathematical Journal
''Duke Mathematical Journal'' is a peer-reviewed mathematics journal published by Duke University Press. It was established in 1935. The founding editors-in-chief were David Widder, Arthur Coble, and Joseph Miller Thomas. The first issue inclu ...
, issn=0012-7094 , volume=81 , issue=2 , pages=269–322
Zeta and L-functions
Conjectures
Unsolved problems in number theory
Analytic number theory
Random matrices