Magnetodynamic Force

In physics, a ponderomotive force is an nonlinear force that a charged particle experiences in an inhomogeneous oscillating electromagnetic field. It causes the particle to move towards the area of the weaker field strength, rather than oscillating around an initial point as happens in a homogeneous field. This occurs because the particle sees a greater magnitude of force during the half of the oscillation period while it is in the area with the stronger field. The net force during its period in the weaker area in the second half of the oscillation does not offset the net force of the first half, and so over a complete cycle this makes the particle accelerate towards the area of lesser force.

The classical expression for the ponderomotive force F_p is
:$\mathbf_=$ $-\frac$ $\nabla$ $(\hat E^2)$
which has units of newtons (in SI units) and where ''e'' is the electrical charge of the particle, ''m'' is its mass, ''ω'' is the angular frequency of oscillation of the field, and $\hat E$ is the amplitude of the electric field. At non-relativistic particle velocities the magnetic field exerts very little force and can be disregarded.

This equation means that a charged particle in an inhomogeneous oscillating field not only oscillates at the frequency of ''ω'' of the field, but is also accelerated by F_p toward the weak field direction. This is a rare case in which the direction of the force does not depend on whether the particle is positively or negatively charged.

Etymology

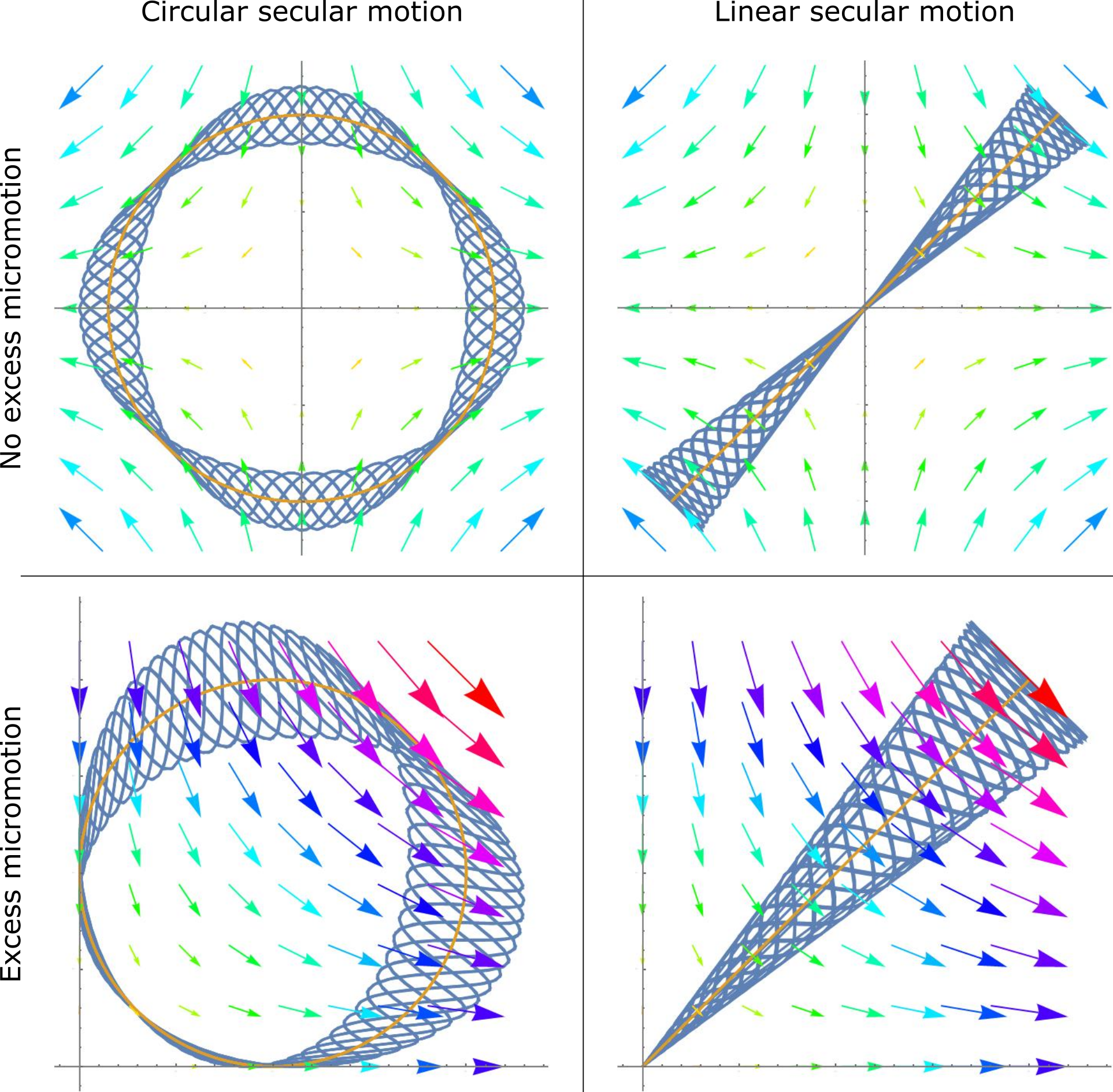
The term ''ponderomotive'' comes from the Latin ''ponder-'' (meaning weight) and the english ''motive'' (having to do with motion).

1D Classical Derivation

A simplified derivation of the ponderomotive force expression proceeds in the one-dimensional case as follows.

Consider a particle under the action of a non-uniform electric field oscillating at frequency $\omega$ in the x-direction, and assume that the particle moves only in the x-direction. Further, also assume the particle always moves at non-relativistic velocities, letting us neglect the magnetic force. The equation of motion is then given by:
:$\ddot = \frac\hat E_x(x)\cos(\omega t).$
If the length scale $\sim L$ of variation of $\hat E_x(x)$ is large enough, then the particle trajectory can be divided into a slow time (secular) motion and a fast time (micro)motion:
:$x=x_0+x_1$
where $x_0$ is the slow drift motion and $x_1$ represents fast oscillations. Now, let us also assume that $x_1 \ll L$. Under this assumption, we can use Taylor expansion on the force equation about $x_0$, to get:
:\ddot_0+\ddot_1 \approx \frac\left hat E_x(x_0)+x_1 \hat E_x'(x_0)\rightcos(\omega t)
:because the oscillation is high frequency $\ddot_0 \ll \ddot_1$, and because $x_1$ is small, $x_1 \hat E_x'(x_0)$ can be neglected, so
:$\ddot_1 \approx \frac\hat E_x(x_0)\cos(\omega t)$

On the time scale on which $x_1$ oscillates, $x_0$ is essentially a constant. Thus, the above can be integrated to get:
:$x_1 \approx -\frac\frac \cos(\omega t)$

Substituting this in the Taylor expanded force equation and averaging over the $2\pi / \omega$ timescale, we get,
:$\ddot_0 \approx -\frac\frac = -\frac(\hat E_x^2) '$
:$\Rightarrow F_p = m\ddot_0=-\frac(\hat E_x^2) ',$

as sinusoids average to 0 and squared sinusoids average to $\frac$. This at least hints at the form of the classical 3D expression.

General expression

Including the magnetic field in the analysis and allowing relativistic velocities and slightly more general fields, the starting point is the exact equations, in four-vector notation:

m \frac = \mathrm\left ^\mu\right= \mathrm\left hat f^\mu(x,u)e^\right

Here $m$ is the mass of the particle, $u$ is the four-velocity, $\tau$ is the proper time, $f$ is the Lorentz force (see four-force), $x$ is the four-position, and $k$ is the wave four-vector. The force is allowed to be complex so that, for example, circularly polarized fields are included.

From these assumptions, the perturbative analysis yields the following ponderomotive force:
$m\frac \approx -\frac$,
where $\bar$ is the time-averaged four-velocity, $\partial^$ are the contravariant components of the four-gradient and $\ ^*$ denotes complex conjugation. The force is a proper four-vector, being the four-gradient of a Lorentz scalar. This can be translated to regular 3-vector notation:
$\frac \approx \frac$
where $\boldsymbol=\boldsymbol/c$, $\bar$ is the time-averaged particle energy in the units of the rest mass, and $\omega - \boldsymbol\cdot\boldsymbol$ can be interpreted as a Doppler-shifted angular frequency. Note that $k$ and $\omega$ do not have to follow any particular dispersion relation. For example in a magnetic undulator, $\omega$ is zero, and in a standing wave $\boldsymbol$ is 0, as the spatial variation must be included in the envelope of $\hat \boldsymbol$.

This expression predicts behaviour that can be significantly different from those predicted by the classical expression. The ponderomotive force can even have a completely opposite direction to that of the classical expression for relativistic particle velocities or for strongly focused fields. Taking $\beta = \frac$ to be very small, the general expression reduces to the classical one. In the limit where the electromagnetic fields are very similar to those of a plane wave, it reduces to an earlier relativistic generalisation found by (among others) Quesnel and Mora in 1998:

$\frac \approx \frac$.

Time averaged density

Instead of a single charged particle, there could be a gas of charged particles confined by the action of such a force. Such a gas of charged particles is called plasma. The distribution function and density of the plasma will fluctuate at the applied oscillating frequency and to obtain an exact solution, we need to solve the Vlasov Equation. But, it is usually assumed that the time averaged density of the plasma can be directly obtained from the expression for the force expression for the drift motion of individual charged particles:
:\bar(x)=n_0 \exp \left \frac \Phi_ (x)\right/math>

where $\Phi_$ is the ponderomotive potential and is given by
:\Phi_ (x)=\frac \left (x)\right2

Applications

The idea of a ponderomotive description of particles under the action of a time-varying field has applications in areas like:

* High harmonic generation
*Plasma acceleration of particles
*Plasma propulsion engine especially the Electrodeless plasma thruster
*Quadrupole ion trap
*Terahertz time-domain spectroscopy as a source of high energy THz radiation in laser-induced air plasmas

The quadrupole ion trap uses a linear function $g(x) = x$ along its principal axes. This gives rise to a harmonic oscillator in the secular motion with the so-called trapping frequency $\Omega \propto \frac$, where $q, m, V, \omega, d_0$ are the charge and mass of the ion, the peak amplitude and the frequency of the radiofrequency (rf) trapping field, and the ion-to-electrode distance respectively. Note that a larger rf frequency lowers the trapping frequency.

The ponderomotive force also plays an important role in laser induced plasmas as a major density lowering factor.

Often, however, the assumed slow-time independency of $\Phi_P$ is too restrictive, an example being the
ultra-short, intense laser pulse-plasma(target) interaction. Here a new ponderomotive effect comes into play,
the ponderomotive memory effect. The result is a weakening of the ponderomotive force and the generation of wake fields and ponderomotive streamers.U. Wolf and H. Schamel,"Wake-field Generation by the Ponderomotive Memory Effect",
Phys. Rev.E 56,4656(1997), doi:10.1103/PhysRevE.56.4656 In this case the fast-time averaged density becomes for a Maxwellian plasma:
\bar n(x,t)= n_0 e^ + \frac \int_^ dv e^ M(x,v,t)/math>,
where $M(x,v,t):=\int_^t d\tau\partial_\tau \Psi(x-v(t-\tau),\tau)$ and $\Psi(x,t):=\frac \Phi_P(x,t)$.

References

;General
*
;Citations

Journals

*
*
*
*
*
*{{cite journal , last1= Bucksbaum , first1= P. H. , last2= Freeman , first2= R. R. , last3= Bashkansky , first3= M. , last4= McIlrath , first4= T. J. , year= 1987 , title= Role of the ponderomotive potential in above-threshold ionization , journal= Journal of the Optical Society of America B, volume= 4 , issue= 5, page= 760 , doi=10.1364/josab.4.000760, bibcode= 1987JOSAB...4..760B , citeseerx= 10.1.1.205.4672

Electrodynamics
Force