MacMahon Squares on:
[Wikipedia]
[Google]
[Amazon]
 MacMahon Squares are an
MacMahon Squares are an
 MacMahon squares was first published in
MacMahon squares was first published in
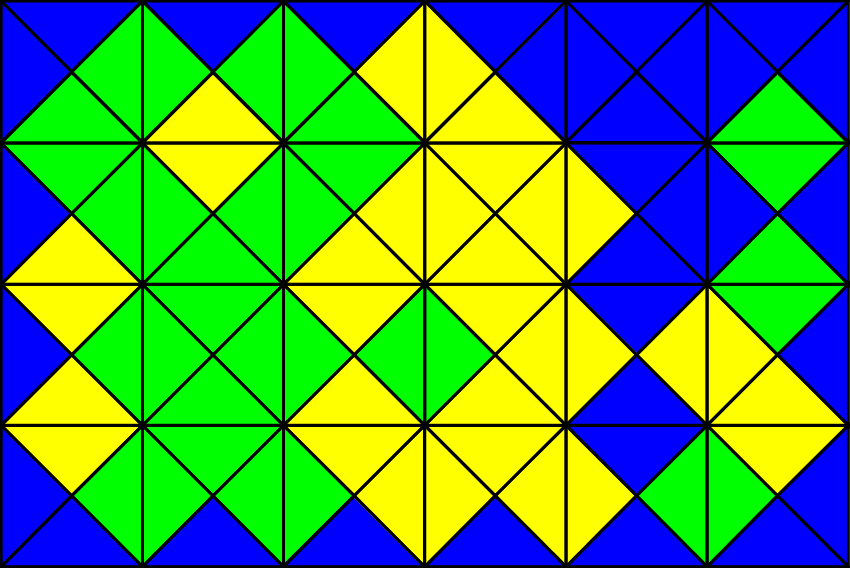
File:MacMahon squares example C1,1,1 B10,10,0.svg, C1,1,1 B10,10,0 (Fig. 27)
File:MacMahon squares example C1,2 B20,0,0.svg, C1,2 B20,0,0 (Fig. 28)
File:MacMahon squares example C1,2 B12,4,4.svg, C1,2 B12,4,4 (Fig. 28)
MacMahon Squares Online
Puzzles
 MacMahon Squares are an
MacMahon Squares are an edge-matching puzzle
An edge-matching puzzle is a type of tiling puzzle involving tiling an area with (typically regular) polygons whose edges are distinguished with colours or patterns, in such a way that the edges of adjacent tiles match.
Edge-matching puzzles are k ...
first published by Percy MacMahon
Percy Alexander MacMahon (26 September 1854 – 25 December 1929) was a mathematician, especially noted in connection with the partitions of numbers and enumerative combinatorics.
Early life
Percy MacMahon was born in Malta to a British mi ...
in 1921, using 24 unique square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length a ...
s with 3-color patterns; each of the four edges is assigned a single color. The complete set of 24 squares are organized next to each other by matching edge color
Color (American English) or colour (British English) is the visual perceptual property deriving from the spectrum of light interacting with the photoreceptor cells of the eyes. Color categories and physical specifications of color are assoc ...
s to create a 4 by 6 grid
Grid, The Grid, or GRID may refer to:
Common usage
* Cattle grid or stock grid, a type of obstacle is used to prevent livestock from crossing the road
* Grid reference, used to define a location on a map
Arts, entertainment, and media
* News g ...
. Such tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of ge ...
puzzles have multiple variants, which are determined by restrictions on how to arrange the 24 squares. This game has also been commercialized in numerous physical forms, by various companies.
The game
Percy Alexander MacMahon
Percy Alexander MacMahon (26 September 1854 – 25 December 1929) was a mathematician, especially noted in connection with the partitions of numbers and enumerative combinatorics.
Early life
Percy MacMahon was born in Malta to a British mi ...
's 1921 treatise ''New Mathematical Pastimes''. The original version consisted of one copy of each of the 24 different squares that can be made by coloring the edges of a square with one of three colors. (Here "different" means up to Two mathematical objects ''a'' and ''b'' are called equal up to an equivalence relation ''R''
* if ''a'' and ''b'' are related by ''R'', that is,
* if ''aRb'' holds, that is,
* if the equivalence classes of ''a'' and ''b'' with respect to ''R'' a ...
rotations.) The goal is to arrange the squares into a 4 by 6 grid so that when two squares share an edge, the common edge is the same color in both squares.
In 1964, a supercomputer was used to produce 12,261 solutions to the basic version of the MacMahon Squares puzzle, with a runtime of about 40 hours.
Theory
The MacMahon Squares game is an example of an edge-matching puzzle. The family of such problems isNP-complete
In computational complexity theory, a problem is NP-complete when:
# it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by tryin ...
. The first part of ''New Mathematical Diversions'' describes these games in general, starting with linear forms (domino
Dominoes is a family of tile-based games played with gaming pieces, commonly known as dominoes. Each domino is a rectangular tile, usually with a line dividing its face into two square ''ends''. Each end is marked with a number of spots (also ca ...
es), then progressing in detail with similar games using tiles shaped as equilateral triangles, squares, right isoceles triangles, cubes, and hexagons.
There are a total of 24 distinct squares for 3 colors. For an arbitrary number of colors , the number of unique squares can be found by the expression .
For other shapes with colors, MacMahon determined the number of unique patterns are:
* Triangle:
* Pentagon:
* Hexagon:
* Heptagon:
For example, given a triangle with three sides, each of which is assigned one of four possible colors, there are 56 unique patterns.
Variants
Contact system
In his book,MacMahon
McMahon, also spelled MacMahon (older Irish orthography: ; reformed Irish orthography: ), is a surname of Irish origin. It is derived from the Gaelic ''Mac'' ''Mathghamhna'' meaning 'son of the bear'.
The surname came into use around the 11th cen ...
suggested the ability to define which borders can contact one another, based on their colors. This is by some permutation of the 3 colors, described by Ca,b,c. Here, a, b, and c represent the shift in colors to which the first, second, and third colors can be matched to. A '1' it is matched to itself, and a '2' signifies that it must be matched with a different color.
For example, C1,1,1 represents 1 to 1, 2 to 2, and 3 to 3, as each of these matchings are represented by the number 1. Alternatively, C1,2 represents 1 to 1 and 2 to 3 as the 1 to 1 matching is represented by the number 1, and the matching between 2 and 3 is represented by 2. More colors can be described in a similar way. For example, a coloring of C1,2,2,2 represents 1 to 1, 2 to 3, 4 to 5, and 6 to 7.
From here we can see that the only possible numbers to describe the pairings by are 1 and 2, since a 3 or above merely skips over a color that would be used the same otherwise because colorings are relative
Relative may refer to:
General use
*Kinship and family, the principle binding the most basic social units society. If two people are connected by circumstances of birth, they are said to be ''relatives''
Philosophy
*Relativism, the concept that ...
.
Boundaries
Another way to change the puzzle is to restrict which colors squared make up the border colors. In the classic MacMahon squares puzzle, there are a total of 20 places on the border. The number of each color that can be present on these 20 places can be described by Ba,b,c where a, b, and c are the number of each color of the border pieces. For example, B20,0,0 represents 20 of the first color and none of the rest since the first color already constitutes all available border spaces. Alternatively, B10,10,0 represents 10 of the first color and 10 of the next. More colors can be described in a similar way. For example, a boundary of B22,16,8,2 represents 22 of the first, 16 of the second, 8 of the next, and 2 of the last colors to populate the border colors. From here we can see that the only possible numbers to describe the number of each color composing the boundary are even numbers, since this would imply an odd number of another color, which would violate theparity
Parity may refer to:
* Parity (computing)
** Parity bit in computing, sets the parity of data for the purpose of error detection
** Parity flag in computing, indicates if the number of set bits is odd or even in the binary representation of the r ...
of the total number of triangles.
Analogous puzzles
MacMahon Squares, along with variations on the idea, was commercialized as Multimatch. Another puzzle with similar properties is MacMahon's Cubes, which are a set of 30 cubes, with sides colored one of 6 different colors. Unlike the MacMahon Squares puzzle, we do not include all 2,226 possible cubes, but only the cubes containing exactly 6 distinct colors and 1 of each of the 6 colors. MacMahon Squares have served as a baseline for numerous other puzzles. Some of these include the Nelson Puzzle, theWang Tile
Wang tiles (or Wang dominoes), first proposed by mathematician, logician, and philosopher Hao Wang in 1961, are a class of formal systems. They are modelled visually by square tiles with a color on each side. A set of such tiles is selected, an ...
, and TetraVex
An edge-matching puzzle is a type of tiling puzzle involving tiling an area with (typically regular) polygons whose edges are distinguished with colours or patterns, in such a way that the edges of adjacent tiles match.
Edge-matching puzzles are k ...
.
The commercial board game '' Trioker'', patented in 1969 by Marc Odier, uses triangular tiles first proposed by MacMahon in 1921.
Notes
References
{{ReflistExternal links
MacMahon Squares Online
Puzzles