Lever Tumbler Lock on:
[Wikipedia]
[Google]
[Amazon]
A lever is a
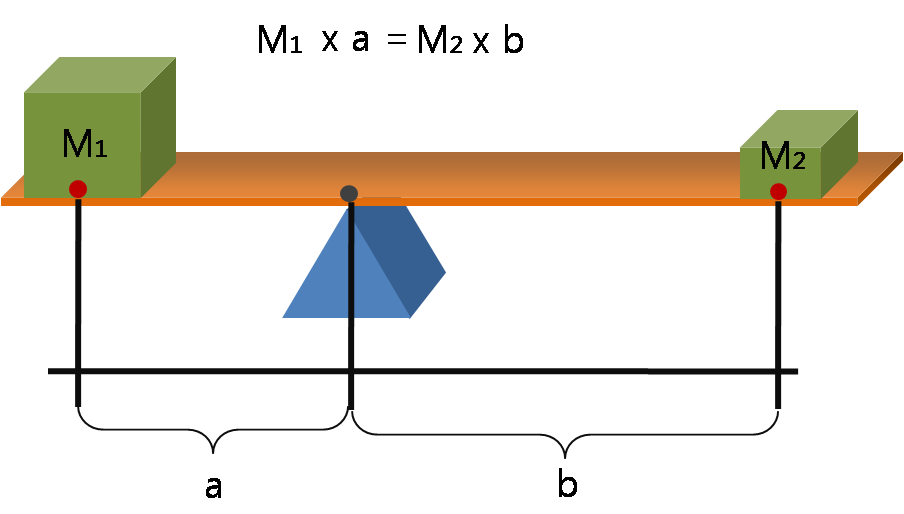 A lever is a beam connected to ground by a hinge, or pivot, called a fulcrum. The ideal lever does not dissipate or store energy, which means there is no friction in the hinge or bending in the beam. In this case, the power into the lever equals the power out, and the ratio of output to input force is given by the ratio of the distances from the fulcrum to the points of application of these forces. This is known as the law of the lever.
The mechanical advantage of a lever can be determined by considering the balance of moments or torque, ''T'', about the fulcrum. If the distance traveled is greater, then the output force is lessened.
where F1 is the input force to the lever and F2 is the output force. The distances ''a'' and ''b'' are the perpendicular distances between the forces and the fulcrum.
Since the moments of torque must be balanced, . So, .
The mechanical advantage of a lever is the ratio of output force to input force.
This relationship shows that the mechanical advantage can be computed from ratio of the distances from the fulcrum to where the input and output forces are applied to the lever, assuming a weightless lever and no losses due to friction, flexibility, or wear. This remains true even though the "horizontal" distance (perpendicular to the pull of gravity) of both ''a'' and ''b'' change (diminish) as the lever changes to any position away from the horizontal.
A lever is a beam connected to ground by a hinge, or pivot, called a fulcrum. The ideal lever does not dissipate or store energy, which means there is no friction in the hinge or bending in the beam. In this case, the power into the lever equals the power out, and the ratio of output to input force is given by the ratio of the distances from the fulcrum to the points of application of these forces. This is known as the law of the lever.
The mechanical advantage of a lever can be determined by considering the balance of moments or torque, ''T'', about the fulcrum. If the distance traveled is greater, then the output force is lessened.
where F1 is the input force to the lever and F2 is the output force. The distances ''a'' and ''b'' are the perpendicular distances between the forces and the fulcrum.
Since the moments of torque must be balanced, . So, .
The mechanical advantage of a lever is the ratio of output force to input force.
This relationship shows that the mechanical advantage can be computed from ratio of the distances from the fulcrum to where the input and output forces are applied to the lever, assuming a weightless lever and no losses due to friction, flexibility, or wear. This remains true even though the "horizontal" distance (perpendicular to the pull of gravity) of both ''a'' and ''b'' change (diminish) as the lever changes to any position away from the horizontal.
 Thus, the ratio of the output force ''F''''B'' to the input force ''F''''A'' is obtained as
which is the mechanical advantage of the lever.
This equation shows that if the distance ''a'' from the fulcrum to the point ''A'' where the input force is applied is greater than the distance ''b'' from fulcrum to the point ''B'' where the output force is applied, then the lever amplifies the input force. If the opposite is true that the distance from the fulcrum to the input point ''A'' is less than from the fulcrum to the output point ''B'', then the lever reduces the magnitude of the input force.
Thus, the ratio of the output force ''F''''B'' to the input force ''F''''A'' is obtained as
which is the mechanical advantage of the lever.
This equation shows that if the distance ''a'' from the fulcrum to the point ''A'' where the input force is applied is greater than the distance ''b'' from fulcrum to the point ''B'' where the output force is applied, then the lever amplifies the input force. If the opposite is true that the distance from the fulcrum to the input point ''A'' is less than from the fulcrum to the output point ''B'', then the lever reduces the magnitude of the input force.
Lever
at Diracdelta science and engineering encyclopedia *
A Simple Lever
' by Stephen Wolfram, Wolfram Demonstrations Project.
Levers: Simple Machines
at EnchantedLearning.com {{Authority control Mechanisms (engineering) Simple machines Ancient inventions Egyptian inventions
simple machine
A simple machine is a machine, mechanical device that changes the Direction (geometry) , direction or Magnitude_(mathematics) , magnitude of a force. In general, they can be defined as the simplest Mechanism (engineering) , mechanisms that use ...
consisting of a beam or rigid rod pivoted at a fixed hinge, or '' fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load, and effort, the lever is divided into three types. It is one of the six simple machine
A simple machine is a machine, mechanical device that changes the Direction (geometry) , direction or Magnitude_(mathematics) , magnitude of a force. In general, they can be defined as the simplest Mechanism (engineering) , mechanisms that use ...
s identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage, which is mechanical advantage gained in the system, equal to the ratio of the output force to the input force. As such, the lever is a mechanical advantage device, trading off force against movement.
Etymology
The word "lever" entered English around 1300 from . This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to , itself from the adjective ''levis'', meaning "light" (as in "not heavy"). The word's primary origin is theProto-Indo-European
Proto-Indo-European (PIE) is the reconstructed common ancestor of the Indo-European language family. No direct record of Proto-Indo-European exists; its proposed features have been derived by linguistic reconstruction from documented Indo-Euro ...
stem , meaning "light", "easy", or "nimble", among other things. The PIE stem also gave rise to the English-language antonym of "heavy", "light".
Lever history
Autumn Stanley argues that the digging stick can be considered the first lever, which would position prehistoric women as the inventors of lever technology. The next earliest known cultural evidence of the application of the lever mechanism dates back to the ancientEgypt
Egypt ( , ), officially the Arab Republic of Egypt, is a country spanning the Northeast Africa, northeast corner of Africa and Western Asia, southwest corner of Asia via the Sinai Peninsula. It is bordered by the Mediterranean Sea to northe ...
, when it was used in a simple balance scale. In ancient Egypt
Ancient Egypt () was a cradle of civilization concentrated along the lower reaches of the Nile River in Northeast Africa. It emerged from prehistoric Egypt around 3150BC (according to conventional Egyptian chronology), when Upper and Lower E ...
, a foot pedal was used for the earliest horizontal frame loom. In Mesopotamia
Mesopotamia is a historical region of West Asia situated within the Tigris–Euphrates river system, in the northern part of the Fertile Crescent. Today, Mesopotamia is known as present-day Iraq and forms the eastern geographic boundary of ...
(modern Iraq) , the shadouf, a crane-like device that uses a lever mechanism, was invented. In ancient Egypt
Ancient Egypt () was a cradle of civilization concentrated along the lower reaches of the Nile River in Northeast Africa. It emerged from prehistoric Egypt around 3150BC (according to conventional Egyptian chronology), when Upper and Lower E ...
, workmen used the lever to move and uplift obelisks weighing more than 100 tons. This is evident from the recesses in the large blocks and the handling bosses that could not be used for any purpose other than for levers.
The earliest remaining writings regarding levers date from the third century BC and were provided, by common belief, by the Greek mathematician Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
, who famously stated "Give me a lever (long enough and a fulcrum on which to place it), and I shall move the world". (The Greek usually attributed to Archimedes does not include details about length of lever or fulcrum, i.e., δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω .) That statement has given rise to the phrase "an Archimedean lever" being adopted for use in many instances, not just regarding mechanics, including abstract concepts about the successful effect of a human behavior or action intended to achieve results that could not have occurred without it.
Force and levers
 A lever is a beam connected to ground by a hinge, or pivot, called a fulcrum. The ideal lever does not dissipate or store energy, which means there is no friction in the hinge or bending in the beam. In this case, the power into the lever equals the power out, and the ratio of output to input force is given by the ratio of the distances from the fulcrum to the points of application of these forces. This is known as the law of the lever.
The mechanical advantage of a lever can be determined by considering the balance of moments or torque, ''T'', about the fulcrum. If the distance traveled is greater, then the output force is lessened.
where F1 is the input force to the lever and F2 is the output force. The distances ''a'' and ''b'' are the perpendicular distances between the forces and the fulcrum.
Since the moments of torque must be balanced, . So, .
The mechanical advantage of a lever is the ratio of output force to input force.
This relationship shows that the mechanical advantage can be computed from ratio of the distances from the fulcrum to where the input and output forces are applied to the lever, assuming a weightless lever and no losses due to friction, flexibility, or wear. This remains true even though the "horizontal" distance (perpendicular to the pull of gravity) of both ''a'' and ''b'' change (diminish) as the lever changes to any position away from the horizontal.
A lever is a beam connected to ground by a hinge, or pivot, called a fulcrum. The ideal lever does not dissipate or store energy, which means there is no friction in the hinge or bending in the beam. In this case, the power into the lever equals the power out, and the ratio of output to input force is given by the ratio of the distances from the fulcrum to the points of application of these forces. This is known as the law of the lever.
The mechanical advantage of a lever can be determined by considering the balance of moments or torque, ''T'', about the fulcrum. If the distance traveled is greater, then the output force is lessened.
where F1 is the input force to the lever and F2 is the output force. The distances ''a'' and ''b'' are the perpendicular distances between the forces and the fulcrum.
Since the moments of torque must be balanced, . So, .
The mechanical advantage of a lever is the ratio of output force to input force.
This relationship shows that the mechanical advantage can be computed from ratio of the distances from the fulcrum to where the input and output forces are applied to the lever, assuming a weightless lever and no losses due to friction, flexibility, or wear. This remains true even though the "horizontal" distance (perpendicular to the pull of gravity) of both ''a'' and ''b'' change (diminish) as the lever changes to any position away from the horizontal.
Types of levers
Levers are classified by the relative positions of the fulcrum, effort, and resistance (or load). It is common to call the input force "effort" and the output force "load" or "resistance". This allows the identification of three classes of levers by the relative locations of the fulcrum, the resistance and the effort: * Class I – Fulcrum is located between the effort and the resistance: The effort is applied on one side of the fulcrum and the resistance (or load) on the other side. For example, a seesaw, a crowbar, a pair ofscissors
Scissors are hand-operated shearing tools. A pair of scissors consists of a pair of blades pivoted so that the sharpened edges slide against each other when the handles (bows) opposite to the pivot are closed. Scissors are used for cutting var ...
, a balance scale, a pair of pliers, and a claw hammer (pulling a nail). With the fulcrum in the middle, the lever's mechanical advantage may be greater than, less than, or even equal to 1.
* Class II – Resistance (or load) is located between the effort and the fulcrum: The effort is applied on one side of the resistance and the fulcrum is located on the other side, e.g. a wheelbarrow, a nutcracker, a bottle opener, a wrench, a pair of bellows, and the brake pedal of a car. Since the load arm is smaller than the effort arm, the lever's mechanical advantage is always greater than 1. It is also called a force multiplier lever.
* Class III – Effort is located between the resistance and the fulcrum: The resistance (or load) is applied on one side of the effort and the fulcrum is located on the other side, e.g. a hoe, a pair of tweezers
Tweezers are small hand tools used for grasping objects too small to be easily handled with the human fingers. Tweezers are thumb-driven forceps most likely derived from tongs used to grab or hold hot objects since the dawn of recorded history. ...
, a hammer
A hammer is a tool, most often a hand tool, consisting of a weighted "head" fixed to a long handle that is swung to deliver an impact to a small area of an object. This can be, for example, to drive nail (fastener), nails into wood, to sh ...
, a pair of tongs
Tongs are a type of tool used to grip and lift objects instead of holding them directly with hands. There are many forms of tongs adapted to their specific use. Design variations include resting points so that the working end of the tongs d ...
, a fishing rod, and the mandible of a human skull. Since the effort arm is smaller than the load arm, the lever's mechanical advantage is always less than 1. It is also called a speed multiplier lever.
These cases are described by the mnemonic ''fre 123'' where the ''f'' fulcrum is between ''r'' and ''e'' for the 1st class lever, the ''r'' resistance is between ''f'' and ''e'' for the 2nd class lever, and the ''e'' effort is between ''f'' and ''r'' for the 3rd class lever.
Compound lever
A compound lever comprises several levers acting in series: the resistance from one lever in a system of levers acts as effort for the next, and thus the applied force is transferred from one lever to the next. Examples of compound levers include scales, nail clippers, and piano keys. The '' malleus'', ''incus
The ''incus'' (: incudes) or anvil in the ear is one of three small bones (ossicles) in the middle ear. The incus receives vibrations from the malleus, to which it is connected laterally, and transmits these to the stapes medially. The incus i ...
'', and '' stapes'' are small bones in the middle ear, connected as compound levers, that transfer sound waves from the eardrum to the oval window of the cochlea.
Law of the lever
The lever is a movable bar that pivots on a fulcrum attached to a fixed point. The lever operates by applying forces at different distances from the fulcrum, or a pivot. As the lever rotates around the fulcrum, points farther from this pivot move faster than points closer to the pivot. Therefore, a force applied to a point farther from the pivot must be less than the force located at a point closer in, because power is the product of force and velocity. If ''a'' and ''b'' are distances from the fulcrum to points ''A'' and ''B'' and the force ''FA'' applied to ''A'' is the input and the force ''FB'' applied at ''B'' is the output, the ratio of the velocities of points ''A'' and ''B'' is given by ''a/b'', so the ratio of the output force to the input force, or mechanical advantage, is given by: This is the ''law of the lever'', which was proven byArchimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
using geometric reasoning. It shows that if the distance ''a'' from the fulcrum to where the input force is applied (point ''A'') is greater than the distance ''b'' from fulcrum to where the output force is applied (point ''B''), then the lever amplifies the input force. On the other hand, if the distance ''a'' from the fulcrum to the input force is less than the distance ''b'' from the fulcrum to the output force, then the lever reduces the input force.
The use of velocity in the static analysis of a lever is an application of the principle of virtual work.
Virtual work and the law of the lever
A lever is modeled as a rigid bar connected to a ground frame by a hinged joint called a fulcrum. The lever is operated by applying an input force F''A'' at a point ''A'' located by the coordinate vector r''A'' on the bar. The lever then exerts an output force F''B'' at the point ''B'' located by r''B''. The rotation of the lever about the fulcrum ''P'' is defined by the rotation angle ''θ'' in radians. Let the coordinate vector of the point ''P'' that defines the fulcrum be r''P'', and introduce the lengths which are the distances from the fulcrum to the input point ''A'' and to the output point ''B'', respectively. Now introduce the unit vectors e''A'' and e''B'' from the fulcrum to the point ''A'' and ''B'', so The velocity of the points ''A'' and ''B'' are obtained as where e''A''⊥ and e''B''⊥ are unit vectors perpendicular to e''A'' and e''B'', respectively. The angle ''θ'' is the generalized coordinate that defines the configuration of the lever, and the generalized force associated with this coordinate is given by where ''F''''A'' and ''F''''B'' are components of the forces that are perpendicular to the radial segments ''PA'' and ''PB''. The principle of virtual work states that at equilibrium the generalized force is zero, that is Thus, the ratio of the output force ''F''''B'' to the input force ''F''''A'' is obtained as
which is the mechanical advantage of the lever.
This equation shows that if the distance ''a'' from the fulcrum to the point ''A'' where the input force is applied is greater than the distance ''b'' from fulcrum to the point ''B'' where the output force is applied, then the lever amplifies the input force. If the opposite is true that the distance from the fulcrum to the input point ''A'' is less than from the fulcrum to the output point ''B'', then the lever reduces the magnitude of the input force.
Thus, the ratio of the output force ''F''''B'' to the input force ''F''''A'' is obtained as
which is the mechanical advantage of the lever.
This equation shows that if the distance ''a'' from the fulcrum to the point ''A'' where the input force is applied is greater than the distance ''b'' from fulcrum to the point ''B'' where the output force is applied, then the lever amplifies the input force. If the opposite is true that the distance from the fulcrum to the input point ''A'' is less than from the fulcrum to the output point ''B'', then the lever reduces the magnitude of the input force.
See also
* * Balance lever coupling * bascule * * * *References
External links
Lever
at Diracdelta science and engineering encyclopedia *
A Simple Lever
' by Stephen Wolfram, Wolfram Demonstrations Project.
Levers: Simple Machines
at EnchantedLearning.com {{Authority control Mechanisms (engineering) Simple machines Ancient inventions Egyptian inventions