In
quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, the particle in a one-dimensional lattice is a problem that occurs in the model of a periodic
crystal lattice
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystal, crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that ...
. The potential is caused by
ion
An ion () is an atom or molecule with a net electrical charge. The charge of an electron is considered to be negative by convention and this charge is equal and opposite to the charge of a proton, which is considered to be positive by convent ...
s in the periodic structure of the crystal creating an
electromagnetic field
An electromagnetic field (also EM field) is a physical field, varying in space and time, that represents the electric and magnetic influences generated by and acting upon electric charges. The field at any point in space and time can be regarde ...
so electrons are subject to a regular potential inside the lattice. It is a generalization of the
free electron model
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quan ...
, which assumes zero potential inside the lattice.
Problem definition
When talking about solid materials, the discussion is mainly around crystals – periodic lattices. Here we will discuss a 1D lattice of positive ions. Assuming the spacing between two ions is , the potential in the lattice will look something like this:
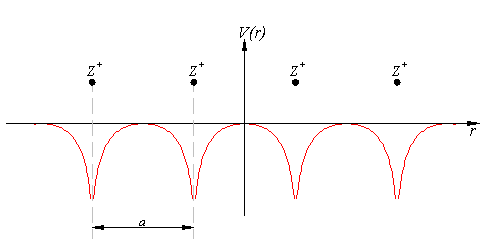
The mathematical representation of the potential is a periodic function with a period . According to
Bloch's theorem
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, ...
,
the wavefunction solution of the
Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
when the potential is periodic, can be written as:
where is a
periodic function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the t ...
which satisfies . It is the Bloch factor with Floquet exponent
which gives rise to the band structure of the energy spectrum of the Schrödinger equation with a periodic potential like the Kronig–Penney potential or a cosine function as it was shown in 1928 by Strutt. The solutions can be given with the help of the
Mathieu functions
In mathematics, Mathieu functions, sometimes called angular Mathieu functions, are solutions of Mathieu's differential equation
:
\frac + (a - 2q\cos(2x))y = 0,
where are real-valued parameters. Since we may add to to change the sign of , i ...
.
When nearing the edges of the lattice, there are problems with the boundary condition. Therefore, we can represent the ion lattice as a ring following the
Born–von Karman boundary conditions. If is the length of the lattice so that , then the number of ions in the lattice is so big, that when considering one ion, its surrounding is almost linear, and the wavefunction of the electron is unchanged. So now, instead of two boundary conditions we get one circular boundary condition:
If is the number of ions in the lattice, then we have the relation: . Replacing in the boundary condition and applying Bloch's theorem will result in a quantization for :
Kronig–Penney model
The Kronig–Penney model (named after
Ralph Kronig
Ralph Kronig (10 March 1904 – 16 November 1995) was a German physicist. He is noted for the discovery of particle spin and for his theory of X-ray absorption spectroscopy. His theories include the Kronig–Penney model, the Coster–Kronig tr ...
and
William Penney
William George Penney, Baron Penney, (24 June 19093 March 1991) was an English mathematician and professor of mathematical physics at the Imperial College London and later the rector of Imperial College London. He had a leading role in the d ...
) is a simple, idealized quantum-mechanical system that consists of an infinite periodic array of
rectangular potential barrier
In quantum mechanics, the rectangular (or, at times, square) potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. ...
s.
The potential function is approximated by a rectangular potential:

Using
Bloch's theorem
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, ...
, we only need to find a solution for a single period, make sure it is continuous and smooth, and to make sure the function is also continuous and smooth.
Considering a single period of the potential:
We have two regions here. We will solve for each independently:
Let ''E'' be an energy value above the well (E>0)
* For
:
*For
 The mathematical representation of the potential is a periodic function with a period . According to
The mathematical representation of the potential is a periodic function with a period . According to  Using
Using  Using
Using