Josephson Relations on:
[Wikipedia]
[Google]
[Amazon]
 In physics, the Josephson effect is a phenomenon that occurs when two superconductors are placed in proximity, with some barrier or restriction between them. It is an example of a macroscopic quantum phenomenon, where the effects of quantum mechanics are observable at ordinary, rather than atomic, scale. The Josephson effect has many practical applications because it exhibits a precise relationship between different physics quantities, such as voltage and frequency, facilitating highly accurate measurements.
The Josephson effect produces a current, known as a
In physics, the Josephson effect is a phenomenon that occurs when two superconductors are placed in proximity, with some barrier or restriction between them. It is an example of a macroscopic quantum phenomenon, where the effects of quantum mechanics are observable at ordinary, rather than atomic, scale. The Josephson effect has many practical applications because it exhibits a precise relationship between different physics quantities, such as voltage and frequency, facilitating highly accurate measurements.
The Josephson effect produces a current, known as a
 Types of Josephson junction include the φ Josephson junction (of which π Josephson junction is a special example), long Josephson junction, and superconducting tunnel junction. A "Dayem bridge" is a thin-film variant of the Josephson junction in which the weak link consists of a superconducting wire with dimensions on the scale of a few micrometres or less. The Josephson junction count of a device is used as a benchmark for its complexity. The Josephson effect has found wide usage, for example in the following areas.
Types of Josephson junction include the φ Josephson junction (of which π Josephson junction is a special example), long Josephson junction, and superconducting tunnel junction. A "Dayem bridge" is a thin-film variant of the Josephson junction in which the weak link consists of a superconducting wire with dimensions on the scale of a few micrometres or less. The Josephson junction count of a device is used as a benchmark for its complexity. The Josephson effect has found wide usage, for example in the following areas.
 The Josephson effect can be calculated using the laws of quantum mechanics. A diagram of a single Josephson junction is shown at right. Assume that superconductor A has Ginzburg–Landau order parameter , and superconductor B , which can be interpreted as the wave functions of Cooper pairs in the two superconductors. If the electric potential difference across the junction is , then the energy difference between the two superconductors is , since each Cooper pair has twice the charge of one electron. The Schrödinger equation for this two-state quantum system is therefore:
where the constant is a characteristic of the junction. To solve the above equation, first calculate the time derivative of the order parameter in superconductor A:
and therefore the Schrödinger equation gives:
The phase difference of Ginzburg-Landau order parameters across the junction is called the Josephson phase:
The Schrödinger equation can therefore be rewritten as:
and its complex conjugate equation is:
Add the two conjugate equations together to eliminate :
Since , we have:
Now, subtract the two conjugate equations to eliminate :
which gives:
Similarly, for superconductor B we can derive that:
Noting that the evolution of Josephson phase is and the time derivative of
The Josephson effect can be calculated using the laws of quantum mechanics. A diagram of a single Josephson junction is shown at right. Assume that superconductor A has Ginzburg–Landau order parameter , and superconductor B , which can be interpreted as the wave functions of Cooper pairs in the two superconductors. If the electric potential difference across the junction is , then the energy difference between the two superconductors is , since each Cooper pair has twice the charge of one electron. The Schrödinger equation for this two-state quantum system is therefore:
where the constant is a characteristic of the junction. To solve the above equation, first calculate the time derivative of the order parameter in superconductor A:
and therefore the Schrödinger equation gives:
The phase difference of Ginzburg-Landau order parameters across the junction is called the Josephson phase:
The Schrödinger equation can therefore be rewritten as:
and its complex conjugate equation is:
Add the two conjugate equations together to eliminate :
Since , we have:
Now, subtract the two conjugate equations to eliminate :
which gives:
Similarly, for superconductor B we can derive that:
Noting that the evolution of Josephson phase is and the time derivative of
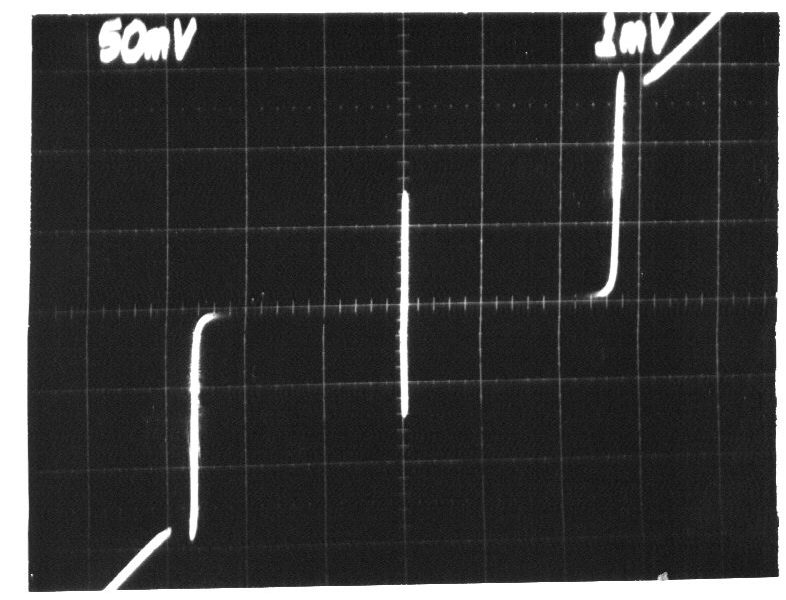 There are three main effects predicted by Josephson that follow directly from the Josephson equations:
There are three main effects predicted by Josephson that follow directly from the Josephson equations:
 In physics, the Josephson effect is a phenomenon that occurs when two superconductors are placed in proximity, with some barrier or restriction between them. It is an example of a macroscopic quantum phenomenon, where the effects of quantum mechanics are observable at ordinary, rather than atomic, scale. The Josephson effect has many practical applications because it exhibits a precise relationship between different physics quantities, such as voltage and frequency, facilitating highly accurate measurements.
The Josephson effect produces a current, known as a
In physics, the Josephson effect is a phenomenon that occurs when two superconductors are placed in proximity, with some barrier or restriction between them. It is an example of a macroscopic quantum phenomenon, where the effects of quantum mechanics are observable at ordinary, rather than atomic, scale. The Josephson effect has many practical applications because it exhibits a precise relationship between different physics quantities, such as voltage and frequency, facilitating highly accurate measurements.
The Josephson effect produces a current, known as a supercurrent
A supercurrent is a superconducting current, that is, electric current which flows without dissipation in a superconductor. Under certain conditions, an electric current can also flow without dissipation in microscopically small non-superconductin ...
, that flows continuously without any voltage applied, across a device known as a Josephson junction (JJ). These consist of two or more superconductors coupled by a weak link. The weak link can be a thin insulating barrier (known as a superconductor–insulator–superconductor junction, or S-I-S), a short section of non-superconducting metal (S-N-S), or a physical constriction that weakens the superconductivity at the point of contact (S-c-S).
Josephson junctions have important applications in quantum-mechanical circuits, such as SQUID
True squid are molluscs with an elongated soft body, large eyes, eight arms, and two tentacles in the superorder Decapodiformes, though many other molluscs within the broader Neocoleoidea are also called squid despite not strictly fitting t ...
s, superconducting qubits
Superconducting quantum computing is a branch of solid state quantum computing which implements superconducting electronic circuits using superconducting qubits as artificial atoms, or quantum dots. For superconducting qubits, the two logic states ...
, and RSFQ
In electronics, rapid single flux quantum (RSFQ) is a digital electronic device that uses superconducting devices, namely Josephson junctions, to process digital signals. In RSFQ logic, information is stored in the form of magnetic flux quanta a ...
digital electronics. The NIST
The National Institute of Standards and Technology (NIST) is an agency of the United States Department of Commerce whose mission is to promote American innovation and industrial competitiveness. NIST's activities are organized into physical sci ...
standard for one volt is achieved by an array of 20,208 Josephson junctions in series.
History
The Josephson effect is named after the British physicist Brian David Josephson, who predicted in 1962 the mathematical relationships for the current and voltage across the weak link. The DC Josephson effect had been seen in experiments prior to 1962, but had been attributed to "super-shorts" or breaches in the insulating barrier leading to the direct conduction of electrons between the superconductors. The first paper to claim the discovery of Josephson's effect, and to make the requisite experimental checks, was that of Philip Anderson and John Rowell. These authors were awarded patents on the effects that were never enforced, but never challenged. Before Josephson's prediction, it was only known that single (i.e. non-paired) electrons can flow through an insulating barrier, by means of quantum tunneling. Josephson was the first to predict the tunneling of superconducting Cooper pairs. For this work, Josephson received the Nobel Prize in Physics in 1973.Applications
SQUID
True squid are molluscs with an elongated soft body, large eyes, eight arms, and two tentacles in the superorder Decapodiformes, though many other molluscs within the broader Neocoleoidea are also called squid despite not strictly fitting t ...
s, or superconducting quantum interference devices, are very sensitive magnetometer
A magnetometer is a device that measures magnetic field or magnetic dipole moment. Different types of magnetometers measure the direction, strength, or relative change of a magnetic field at a particular location. A compass is one such device, o ...
s that operate via the Josephson effect. They are widely used in science and engineering.
In precision metrology
Metrology is the scientific study of measurement. It establishes a common understanding of units, crucial in linking human activities. Modern metrology has its roots in the French Revolution's political motivation to standardise units in Fran ...
, the Josephson effect provides an exactly reproducible conversion between frequency and voltage. Since the frequency is already defined precisely and practically by the caesium standard
The caesium standard is a primary frequency standard in which the Absorption (electromagnetic radiation), photon absorption by transitions between the two hyperfine level, hyperfine ground states of caesium-133 atoms is used to control the output ...
, the Josephson effect is used, for most practical purposes, to give the standard representation of a volt, the Josephson voltage standard
A Josephson voltage standard is a complex system that uses a superconducting integrated circuit chip operating at a temperature of 4 K to generate stable voltages that depend only on an applied frequency and fundamental constants. It is an int ...
.
Single-electron transistors are often constructed of superconducting materials, allowing use to be made of the Josephson effect to achieve novel effects. The resulting device is called a "superconducting single-electron transistor".
The Josephson effect is also used for the most precise measurements of elementary charge
The elementary charge, usually denoted by is the electric charge carried by a single proton or, equivalently, the magnitude of the negative electric charge carried by a single electron, which has charge −1 . This elementary charge is a fundame ...
in terms of the Josephson constant and von Klitzing constant which is related to the quantum Hall effect.
RSFQ
In electronics, rapid single flux quantum (RSFQ) is a digital electronic device that uses superconducting devices, namely Josephson junctions, to process digital signals. In RSFQ logic, information is stored in the form of magnetic flux quanta a ...
digital electronics is based on shunted Josephson junctions. In this case, the junction switching event is associated to the emission of one magnetic flux quantum that carries the digital information: the absence of switching is equivalent to 0, while one switching event carries a 1.
Josephson junctions are integral in superconducting quantum computing as qubits such as in a flux qubit or others schemes where the phase and charge act as the conjugate variables
Conjugate variables are pairs of variables mathematically defined in such a way that they become Fourier transform duals, or more generally are related through Pontryagin duality. The duality relations lead naturally to an uncertainty relation— ...
.
Superconducting tunnel junction detectors (STJs) may become a viable replacement for CCDs ( charge-coupled devices) for use in astronomy and astrophysics
Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline said, Astrophysics "seeks to ascertain the nature of the h ...
in a few years. These devices are effective across a wide spectrum from ultraviolet to infrared, and also in x-rays. The technology has been tried out on the William Herschel Telescope in the SCAM instrument.
Quiteron
Sadeg M. Faris is a Libyan-American engineer and entrepreneur.
Early life and education
Sadeg Faris was brought up in Tripoli in a poor family. His father died when he was ten years old and he was raised with his mother. He won a scholarship from ...
s and similar superconducting switching devices.
Josephson effect has also been observed in superfluid helium quantum interference devices ( SHeQUIDs), the superfluid helium analog of a dc-SQUID.
The Josephson equations
charge carrier density
Charge carrier density, also known as carrier concentration, denotes the number of charge carriers in per volume. In SI units, it is measured in m−3. As with any density, in principle it can depend on position. However, usually carrier concentr ...
is proportional to current , the above solution yields the Josephson equations:
where and are the voltage across and the current through the Josephson junction, and is a parameter of the junction named the critical current. Equation (1) is called the first Josephson relation or weak-link current-phase relation, and equation (2) is called the second Josephson relation or superconducting phase evolution equation. The critical current of the Josephson junction depends on the properties of the superconductors, and can also be affected by environmental factors like temperature and externally applied magnetic field.
The Josephson constant is defined as:
and its inverse is the magnetic flux quantum:
The superconducting phase evolution equation can be reexpressed as:
If we define:
then the voltage across the junction is:
which is very similar to Faraday's law of induction
Faraday's law of induction (briefly, Faraday's law) is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (emf)—a phenomenon known as electromagnetic inducti ...
. But note that this voltage does not come from magnetic energy, since there is no magnetic field in the superconductors; Instead, this voltage comes from the kinetic energy of the carriers (i.e. the Cooper pairs). This phenomenon is also known as kinetic inductance
Kinetic inductance is the manifestation of the inertial mass of mobile charge carriers in alternating electric fields as an equivalent series inductance. Kinetic inductance is observed in high carrier mobility conductors (e.g. superconductors) and ...
.
Three main effects
The DC Josephson effect
The DC Josephson effect is a direct current crossing the insulator in the absence of any external electromagnetic field, owing to tunneling. This DC Josephson current is proportional to the sine of the Josephson phase (phase difference across the insulator, which stays constant over time), and may take values between and .The AC Josephson effect
With a fixed voltage across the junction, the phase will vary linearly with time and the current will be a sinusoidal AC ( Alternating Current) with amplitude and frequency . This means a Josephson junction can act as a perfect voltage-to-frequency converter.The inverse AC Josephson effect
Microwave radiation of a single (angular) frequency can induce quantized DC voltages across the Josephson junction, in which case the Josephson phase takes the form , and the voltage and current across the junction will be: The DC components are: This means a Josephson junction can act like a perfect frequency-to-voltage converter, which is the theoretical basis for theJosephson voltage standard
A Josephson voltage standard is a complex system that uses a superconducting integrated circuit chip operating at a temperature of 4 K to generate stable voltages that depend only on an applied frequency and fundamental constants. It is an int ...
.
Josephson inductance
When the current and Josephson phase varies over time, the voltage drop across the junction will also vary accordingly; As shown in derivation below, the Josephson relations determine that this behavior can be modeled by akinetic inductance
Kinetic inductance is the manifestation of the inertial mass of mobile charge carriers in alternating electric fields as an equivalent series inductance. Kinetic inductance is observed in high carrier mobility conductors (e.g. superconductors) and ...
named Josephson Inductance.
Rewrite the Josephson relations as:
:
Now, apply the chain rule to calculate the time derivative of the current:
:
Rearrange the above result in the form of the current–voltage characteristic of an inductor:
:
This gives the expression for the kinetic inductance as a function of the Josephson Phase:
:
Here, is a characteristic parameter of the Josephson junction, named the Josephson Inductance.
Note that although the kinetic behavior of the Josephson junction is similar to that of an inductor, there is no associated magnetic field. This behaviour is derived from the kinetic energy of the charge carriers, instead of the energy in a magnetic field.
Josephson energy
Based on the similarity of the Josephson junction to a non-linear inductor, the energy stored in a Josephson junction when a supercurrent flows through it can be calculated. The supercurrent flowing through the junction is related to the Josephson phase by the current-phase relation (CPR): : The superconducting phase evolution equation is analogous to Faraday's law: : Assume that at time , the Josephson phase is ; At a later time , the Josephson phase evolved to . The energy increase in the junction is equal to the work done on the junction: : This shows that the change of energy in the Josephson junction depends only on the initial and final state of the junction and not the path. Therefore the energy stored in a Josephson junction is astate function
In the thermodynamics of equilibrium, a state function, function of state, or point function for a thermodynamic system is a mathematical function relating several state variables or state quantities (that describe equilibrium states of a system ...
, which can be defined as:
:
Here is a characteristic parameter of the Josephson junction, named the Josephson Energy. It is related to the Josephson Inductance by . An alternative but equivalent definition is also often used.
Again, note that a non-linear magnetic coil inductor accumulates potential energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Common types of potential energy include the gravitational potentia ...
in its magnetic field when a current passes through it; However, in the case of Josephson junction, no magnetic field is created by a supercurrent — the stored energy comes from the kinetic energy of the charge carriers instead.
The RCSJ model
The Resistively Capacitance Shunted Junction (RCSJ) model, or simply shunted junction model, includes the effect of AC impedance of an actual Josephson junction on top of the two basic Josephson relations stated above. As per Thévenin's theorem, the AC impedance of the junction can be represented by a capacitor and a shunt resistor, both parallel to the ideal Josephson Junction. The complete expression for the current drive becomes: : where the first term is displacement current with - effective capacitance, and the third is normal current with - effective resistance of the junction.Josephson penetration depth
The Josephson penetration depth characterizes the typical length on which an externally appliedmagnetic field
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to ...
penetrates into the long Josephson junction. It is usually denoted as and is given by the following expression (in SI):
:
where is the magnetic flux quantum, is the critical supercurrent density (A/m2), and characterizes the inductance of the superconducting electrodes
:
where is the thickness of the Josephson barrier (usually insulator), and are the thicknesses of superconducting electrodes, and and are their London penetration depths. The Josephson penetration depth usually ranges from a few μm
The micrometre ( international spelling as used by the International Bureau of Weights and Measures; SI symbol: μm) or micrometer (American spelling), also commonly known as a micron, is a unit of length in the International System of Unit ...
to several mm if the critical supercurrent density is very low.
See also
*Pi Josephson junction
A Josephson junction is a quantum mechanical device which is made of two superconducting electrodes separated by a barrier (thin insulating tunnel barrier, normal metal, semiconductor, ferromagnet, etc.).
A Josephson junction is a Josephson junc ...
* φ Josephson junction
* Josephson diode
* Andreev reflection
* Fractional vortices
* Ginzburg–Landau theory
* Macroscopic quantum phenomena
* Macroscopic quantum self-trapping
*Quantum computer
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Though ...
* Quantum gyroscope
* Rapid single flux quantum (RSFQ)
* Semifluxon
*Zero-point energy
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly Quantum fluctuation, fluctuate in their lowest energy state as described by the Heisen ...
*Josephson vortex
In superconductivity, a Josephson vortex (after Brian Josephson from Cambridge University) is a quantum vortex of supercurrents in a Josephson junction (see Josephson effect). The supercurrents circulate around the vortex center which is situated i ...
References
{{Authority control Condensed matter physics Superconductivity Sensors Mesoscopic physics Energy (physics)