Jaccard index on:
[Wikipedia]
[Google]
[Amazon]
The Jaccard index is a
 Instead, a generalization that is continuous between probability distributions and their corresponding support sets is
:
which is called the "Probability" Jaccard. It has the following bounds against the Weighted Jaccard on probability vectors.
:
Here the upper bound is the (weighted) Sørensen–Dice coefficient.
The corresponding distance, , is a metric over probability distributions, and a pseudo-metric over non-negative vectors.
The Probability Jaccard Index has a geometric interpretation as the area of an intersection of
Instead, a generalization that is continuous between probability distributions and their corresponding support sets is
:
which is called the "Probability" Jaccard. It has the following bounds against the Weighted Jaccard on probability vectors.
:
Here the upper bound is the (weighted) Sørensen–Dice coefficient.
The corresponding distance, , is a metric over probability distributions, and a pseudo-metric over non-negative vectors.
The Probability Jaccard Index has a geometric interpretation as the area of an intersection of
 Consider the problem of constructing random variables such that they collide with each other as much as possible. That is, if and , we would like to construct and to maximize
Consider the problem of constructing random variables such that they collide with each other as much as possible. That is, if and , we would like to construct and to maximize
statistic
A statistic (singular) or sample statistic is any quantity computed from values in a sample which is considered for a statistical purpose. Statistical purposes include estimating a population parameter, describing a sample, or evaluating a hypot ...
used for gauging the similarity and diversity
Diversity, diversify, or diverse may refer to:
Business
*Diversity (business), the inclusion of people of different identities (ethnicity, gender, age) in the workforce
*Diversity marketing, marketing communication targeting diverse customers
* ...
of sample sets.
It is defined in general taking the ratio of two sizes (areas or volumes), the intersection size divided by the union size, also called intersection over union (IoU).
It was developed by Grove Karl Gilbert
Grove Karl Gilbert (May 6, 1843 – May 1, 1918), known by the abbreviated name G. K. Gilbert in academic literature, was an American geologist.
Biography
Gilbert was born in Rochester, New York, and graduated from the University of Rochester. ...
in 1884 as his ratio of verification (v) and now is often called the critical success index in meteorology. It was later developed independently by Paul Jaccard, originally giving the French name (coefficient of community), and independently formulated again by Taffee Tadashi Tanimoto. Thus, it is also called Tanimoto index or Tanimoto coefficient in some fields.
Overview
The Jaccard index measures similarity between finite non-empty sample sets and is defined as the size of theintersection
In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their ...
divided by the size of the union of the sample sets:
:
Note that by design, If the sets and have no elements in common, their intersection is empty, so and therefore The other extreme is that the two sets are equal. In that case so then The Jaccard index is widely used in computer science, ecology, genomics and other sciences where binary or binarized data are used. Both the exact solution and approximation methods are available for hypothesis testing with the Jaccard index.
Jaccard similarity also applies to bags, i.e., multiset
In mathematics, a multiset (or bag, or mset) is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the ''multiplicity'' of ...
s. This has a similar formula, but the symbols used represent bag intersection and bag sum (not union). The maximum value is 1/2.
:
The Jaccard distance, which measures ''dis''similarity between sample sets, is complementary to the Jaccard index and is obtained by subtracting the Jaccard index from 1 or, equivalently, by dividing the difference of the sizes of the union and the intersection of two sets by the size of the union:
:
An alternative interpretation of the Jaccard distance is as the ratio of the size of the symmetric difference
In mathematics, the symmetric difference of two sets, also known as the disjunctive union and set sum, is the set of elements which are in either of the sets, but not in their intersection. For example, the symmetric difference of the sets \ and ...
to the union.
Jaccard distance is commonly used to calculate an matrix for clustering and multidimensional scaling
Multidimensional scaling (MDS) is a means of visualizing the level of similarity of individual cases of a data set. MDS is used to translate distances between each pair of n objects in a set into a configuration of n points mapped into an ...
of ''n'' sample sets.
This distance is a metric
Metric or metrical may refer to:
Measuring
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
...
on the collection of all finite sets.
There is also a version of the Jaccard distance for measures, including probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a σ-algebra that satisfies Measure (mathematics), measure properties such as ''countable additivity''. The difference between a probability measure an ...
s. If is a measure on a measurable space
In mathematics, a measurable space or Borel space is a basic object in measure theory. It consists of a set and a σ-algebra, which defines the subsets that will be measured.
It captures and generalises intuitive notions such as length, area, an ...
, then we define the Jaccard index by
:
and the Jaccard distance by
:
Care must be taken if or , since these formulas are not well defined in these cases.
The MinHash min-wise independent permutations locality sensitive hashing scheme may be used to efficiently compute an accurate estimate of the Jaccard similarity index of pairs of sets, where each set is represented by a constant-sized signature derived from the minimum values of a hash function
A hash function is any Function (mathematics), function that can be used to map data (computing), data of arbitrary size to fixed-size values, though there are some hash functions that support variable-length output. The values returned by a ...
.
Similarity of asymmetric binary attributes
Given two objects, ''A'' and ''B'', each with ''n'' binary attributes, the Jaccard index is a useful measure of the overlap that ''A'' and ''B'' share with their attributes. Each attribute of ''A'' and ''B'' can either be 0 or 1. The total number of each combination of attributes for both ''A'' and ''B'' are specified as follows: : represents the total number of attributes where ''A'' and ''B'' both have a value of 1. : represents the total number of attributes where the attribute of ''A'' is 0 and the attribute of ''B'' is 1. : represents the total number of attributes where the attribute of ''A'' is 1 and the attribute of ''B'' is 0. : represents the total number of attributes where ''A'' and ''B'' both have a value of 0. Each attribute must fall into one of these four categories, meaning that : The Jaccard similarity index, ''J'', is given as : The Jaccard distance, ''d''''J'', is given as : Statistical inference can be made based on the Jaccard similarity index, and consequently related metrics. Given two sample sets ''A'' and ''B'' with ''n'' attributes, a statistical test can be conducted to see if an overlap is statistically significant. The exact solution is available, although computation can be costly as ''n'' increases. Estimation methods are available either by approximating amultinomial distribution In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided die rolled ''n'' times. For ''n'' statistical independence, indepen ...
or by bootstrapping.
Difference with the simple matching index (SMC)
When used for binary attributes, the Jaccard index is very similar to the simple matching coefficient. The main difference is that the SMC has the term in its numerator and denominator, whereas the Jaccard index does not. Thus, the SMC counts both mutual presences (when an attribute is present in both sets) and mutual absence (when an attribute is absent in both sets) as matches and compares it to the total number of attributes in the universe, whereas the Jaccard index only counts mutual presence as matches and compares it to the number of attributes that have been chosen by at least one of the two sets. In market basket analysis, for example, the basket of two consumers who we wish to compare might only contain a small fraction of all the available products in the store, so the SMC will usually return very high values of similarities even when the baskets bear very little resemblance, thus making the Jaccard index a more appropriate measure of similarity in that context. For example, consider a supermarket with 1000 products and two customers. The basket of the first customer contains salt and pepper and the basket of the second contains salt and sugar. In this scenario, the similarity between the two baskets as measured by the Jaccard index would be 1/3, but the similarity becomes 0.998 using the SMC. In other contexts, where 0 and 1 carry equivalent information (symmetry), the SMC is a better measure of similarity. For example, vectors of demographic variables stored in dummy variables, such as gender, would be better compared with the SMC than with the Jaccard index since the impact of gender on similarity should be equal, independently of whether male is defined as a 0 and female as a 1 or the other way around. However, when we have symmetric dummy variables, one could replicate the behaviour of the SMC by splitting the dummies into two binary attributes (in this case, male and female), thus transforming them into asymmetric attributes, allowing the use of the Jaccard index without introducing any bias. The SMC remains, however, more computationally efficient in the case of symmetric dummy variables since it does not require adding extra dimensions.Weighted Jaccard similarity and distance
If and are two vectors with all real , then their Jaccard similarity index (also known then as Ruzicka similarity) is defined as : and Jaccard distance (also known then as Soergel distance) : With even more generality, if and are two non-negative measurable functions on a measurable space with measure , then we can define : where and are pointwise operators. Then Jaccard distance is : Then, for example, for two measurable sets , we have where and are the characteristic functions of the corresponding set.Probability Jaccard similarity and distance
The weighted Jaccard similarity described above generalizes the Jaccard Index to positive vectors, where a set corresponds to a binary vector given by theindicator function
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , then the indicator functio ...
, i.e. . However, it does not generalize the Jaccard Index to probability distributions, where a set corresponds to a uniform probability distribution, i.e.
:
It is always less if the sets differ in size. If , and then
:
 Instead, a generalization that is continuous between probability distributions and their corresponding support sets is
:
which is called the "Probability" Jaccard. It has the following bounds against the Weighted Jaccard on probability vectors.
:
Here the upper bound is the (weighted) Sørensen–Dice coefficient.
The corresponding distance, , is a metric over probability distributions, and a pseudo-metric over non-negative vectors.
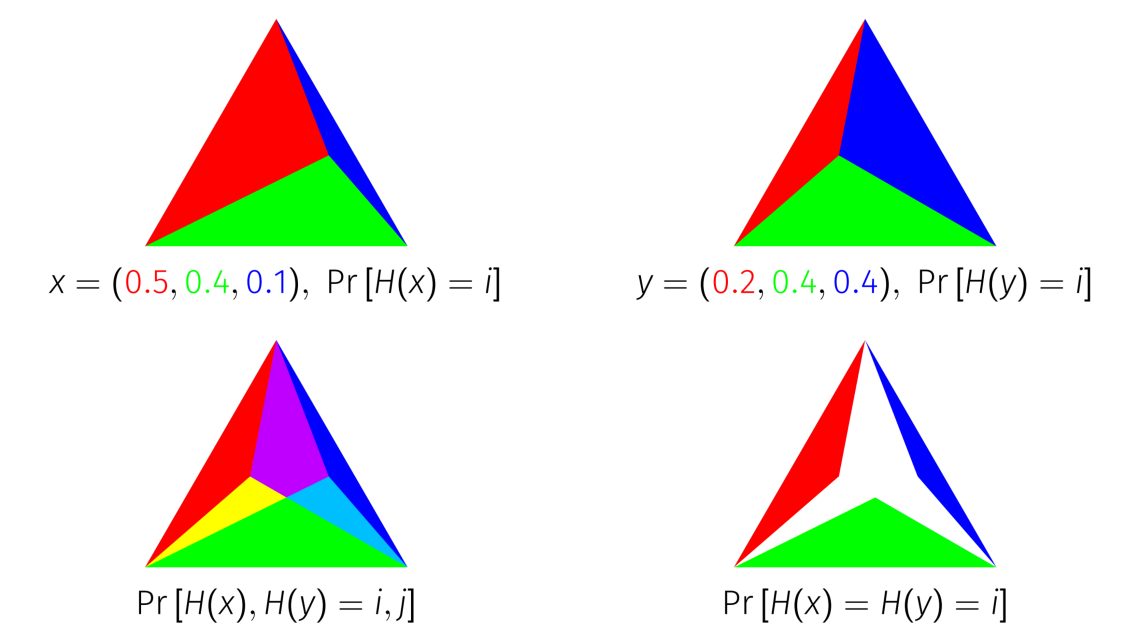
The Probability Jaccard Index has a geometric interpretation as the area of an intersection of
Instead, a generalization that is continuous between probability distributions and their corresponding support sets is
:
which is called the "Probability" Jaccard. It has the following bounds against the Weighted Jaccard on probability vectors.
:
Here the upper bound is the (weighted) Sørensen–Dice coefficient.
The corresponding distance, , is a metric over probability distributions, and a pseudo-metric over non-negative vectors.
The Probability Jaccard Index has a geometric interpretation as the area of an intersection of simplices
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
. Every point on a unit -simplex corresponds to a probability distribution on elements, because the unit -simplex is the set of points in dimensions that sum to 1. To derive the Probability Jaccard Index geometrically, represent a probability distribution as the unit simplex divided into sub simplices according to the mass of each item. If you overlay two distributions represented in this way on top of each other, and intersect the simplices corresponding to each item, the area that remains is equal to the Probability Jaccard Index of the distributions.
Optimality of the Probability Jaccard Index
 Consider the problem of constructing random variables such that they collide with each other as much as possible. That is, if and , we would like to construct and to maximize
Consider the problem of constructing random variables such that they collide with each other as much as possible. That is, if and , we would like to construct and to maximize