Inscribed angle on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 The inscribed angle theorem states that an angle ''θ'' inscribed in a circle is half of the central angle 2''θ'' that
The inscribed angle theorem states that an angle ''θ'' inscribed in a circle is half of the central angle 2''θ'' that
 Let ''O'' be the center of a circle, as in the diagram at right. Choose two points on the circle, and call them ''V'' and ''A''. Draw line ''VO'' and extended past ''O'' so that it intersects the circle at point ''B'' which is diametrically opposite the point ''V''. Draw an angle whose vertex is point ''V'' and whose sides pass through points ''A'' and ''B''.
Draw line ''OA''. Angle ''BOA'' is a central angle; call it ''θ''. Lines ''OV'' and ''OA'' are both radii of the circle, so they have equal lengths. Therefore, triangle ''VOA'' is isosceles, so angle ''BVA'' (the inscribed angle) and angle ''VAO'' are equal; let each of them be denoted as ''ψ''.
Angles ''BOA'' and ''AOV'' add up to 180°, since line ''VB'' passing through ''O'' is a straight line. Therefore, angle ''AOV'' measures 180° − ''θ''.
It is known that the three angles of a
Let ''O'' be the center of a circle, as in the diagram at right. Choose two points on the circle, and call them ''V'' and ''A''. Draw line ''VO'' and extended past ''O'' so that it intersects the circle at point ''B'' which is diametrically opposite the point ''V''. Draw an angle whose vertex is point ''V'' and whose sides pass through points ''A'' and ''B''.
Draw line ''OA''. Angle ''BOA'' is a central angle; call it ''θ''. Lines ''OV'' and ''OA'' are both radii of the circle, so they have equal lengths. Therefore, triangle ''VOA'' is isosceles, so angle ''BVA'' (the inscribed angle) and angle ''VAO'' are equal; let each of them be denoted as ''ψ''.
Angles ''BOA'' and ''AOV'' add up to 180°, since line ''VB'' passing through ''O'' is a straight line. Therefore, angle ''AOV'' measures 180° − ''θ''.
It is known that the three angles of a
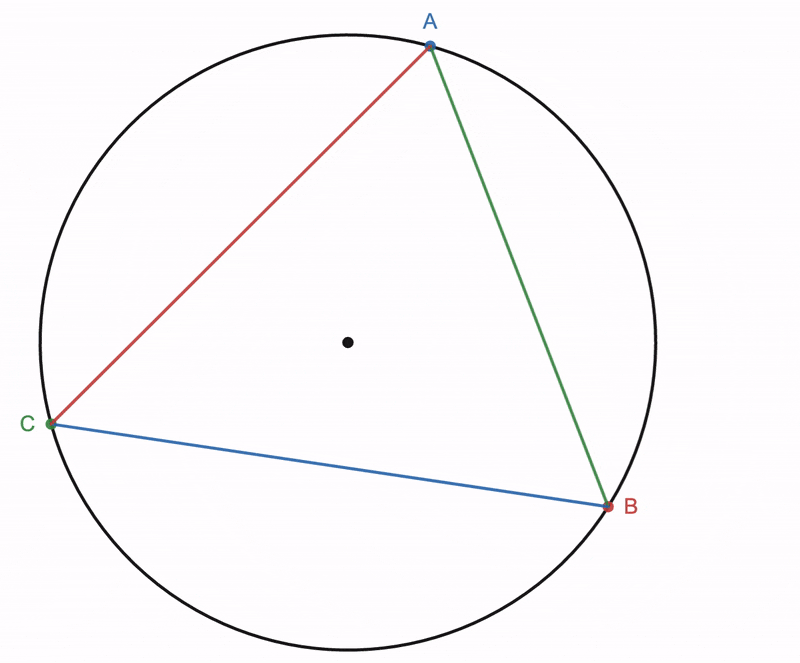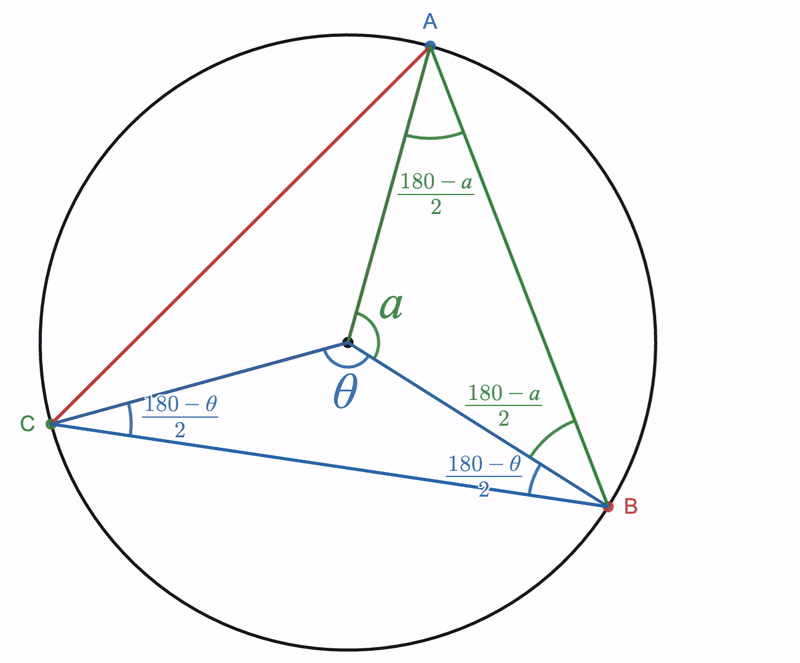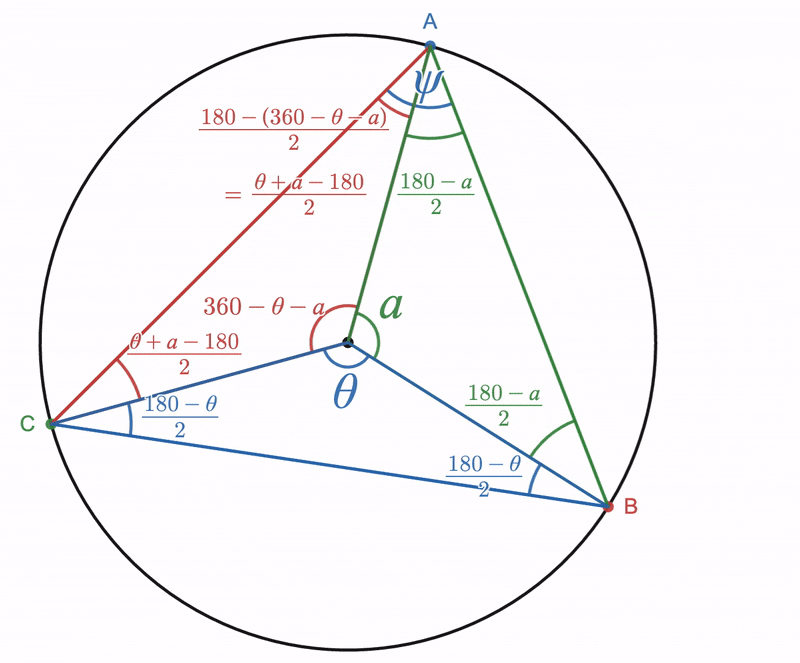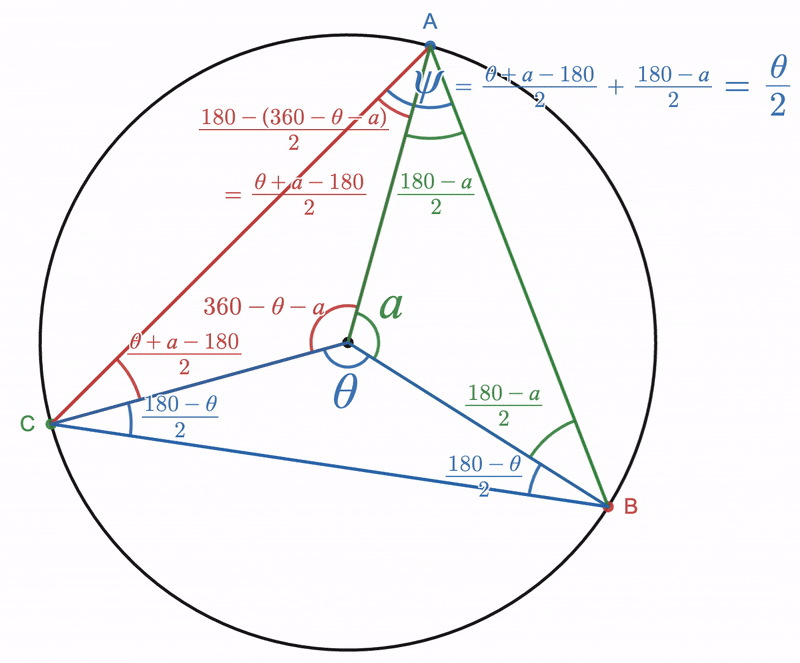
 Given a circle whose center is point ''O'', choose three points ''V'', ''C'', and ''D'' on the circle. Draw lines ''VC'' and ''VD'': angle ''DVC'' is an inscribed angle. Now draw line ''VO'' and extend it past point ''O'' so that it intersects the circle at point ''E''. Angle ''DVC'' subtends arc ''DC'' on the circle.
Suppose this arc includes point ''E'' within it. Point ''E'' is diametrically opposite to point ''V''. Angles ''DVE'' and ''EVC'' are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore,
:
then let
:
:
:
so that
:
Draw lines ''OC'' and ''OD''. Angle ''DOC'' is a central angle, but so are angles ''DOE'' and ''EOC'', and
:
Let
:
:
:
so that
:
From Part One we know that and that . Combining these results with equation (2) yields
:
therefore, by equation (1),
:
Given a circle whose center is point ''O'', choose three points ''V'', ''C'', and ''D'' on the circle. Draw lines ''VC'' and ''VD'': angle ''DVC'' is an inscribed angle. Now draw line ''VO'' and extend it past point ''O'' so that it intersects the circle at point ''E''. Angle ''DVC'' subtends arc ''DC'' on the circle.
Suppose this arc includes point ''E'' within it. Point ''E'' is diametrically opposite to point ''V''. Angles ''DVE'' and ''EVC'' are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore,
:
then let
:
:
:
so that
:
Draw lines ''OC'' and ''OD''. Angle ''DOC'' is a central angle, but so are angles ''DOE'' and ''EOC'', and
:
Let
:
:
:
so that
:
From Part One we know that and that . Combining these results with equation (2) yields
:
therefore, by equation (1),
:
Relationship Between Central Angle and Inscribed Angle
Munching on Inscribed Angles
at cut-the-knot
Arc Central Angle
With interactive animation
With interactive animation
With interactive animation
At bookofproofs.org
{{Ancient Greek mathematics Euclidean plane geometry Angle Theorems about circles Articles containing proofs
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, an inscribed angle is the angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ...
formed in the interior of a circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle.
Equivalently, an inscribed angle is defined by two chords of the circle sharing an endpoint.
The inscribed angle theorem relates the measure of an inscribed angle to that of the central angle subtending the same arc.
The inscribed angle theorem appears as Proposition 20 on Book 3 of Euclid's ''Elements''.
Theorem
Statement
 The inscribed angle theorem states that an angle ''θ'' inscribed in a circle is half of the central angle 2''θ'' that
The inscribed angle theorem states that an angle ''θ'' inscribed in a circle is half of the central angle 2''θ'' that subtend
In geometry, an angle is subtended by an arc, line segment or any other section of a curve when its two rays pass through the endpoints of that arc, line segment or curve section. Conversely, the arc, line segment or curve section confined with ...
s the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the circle.
Proof
Inscribed angles where one chord is a diameter
triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC.
In Euclidean geometry, any three points, when non- colli ...
add up to 180°, and the three angles of triangle ''VOA'' are:
: 180° − ''θ''
: ''ψ''
: ''ψ''.
Therefore,
:
Subtract
:
from both sides,
:
where ''θ'' is the central angle subtending arc ''AB'' and ''ψ'' is the inscribed angle subtending arc ''AB''.
Inscribed angles with the center of the circle in their interior
Inscribed angles with the center of the circle in their exterior
The previous case can be extended to cover the case where the measure of the inscribed angle is the ''difference'' between two inscribed angles as discussed in the first part of this proof. Given a circle whose center is point ''O'', choose three points ''V'', ''C'', and ''D'' on the circle. Draw lines ''VC'' and ''VD'': angle ''DVC'' is an inscribed angle. Now draw line ''VO'' and extend it past point ''O'' so that it intersects the circle at point ''E''. Angle ''DVC'' subtends arc ''DC'' on the circle. Suppose this arc does not include point ''E'' within it. Point ''E'' is diametrically opposite to point ''V''. Angles ''EVD'' and ''EVC'' are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them. Therefore, :. then let : : : so that : Draw lines ''OC'' and ''OD''. Angle ''DOC'' is a central angle, but so are angles ''EOD'' and ''EOC'', and : Let : : : so that : From Part One we know that and that . Combining these results with equation (4) yields : therefore, by equation (3), :
Corollary
By a similar argument, the angle between achord
Chord may refer to:
* Chord (music), an aggregate of musical pitches sounded simultaneously
** Guitar chord a chord played on a guitar, which has a particular tuning
* Chord (geometry), a line segment joining two points on a curve
* Chord ( ...
and the tangent line at one of its intersection points equals half of the central angle subtended by the chord. See also Tangent lines to circles
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
.
Applications
The inscribed angle theorem is used in many proofs of elementary Euclidean geometry of the plane. A special case of the theorem is Thales' theorem, which states that the angle subtended by adiameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid fo ...
is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of cyclic quadrilaterals sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the power of a point
In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826.
Specifically, the power \Pi(P) of a point P with respect ...
with respect to a circle. Further, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal.
Inscribed angle theorems for ellipses, hyperbolas and parabolas
Inscribed angle theorems exist for ellipses, hyperbolas and parabolas, too. The essential differences are the measurements of an angle. (An angle is considered a pair of intersecting lines.) * Ellipse * Hyperbola * ParabolaReferences
* * *External links
*Relationship Between Central Angle and Inscribed Angle
Munching on Inscribed Angles
at cut-the-knot
Arc Central Angle
With interactive animation
With interactive animation
With interactive animation
At bookofproofs.org
{{Ancient Greek mathematics Euclidean plane geometry Angle Theorems about circles Articles containing proofs