Information Set (game Theory) on:
[Wikipedia]
[Google]
[Amazon]
In  In games with
In games with

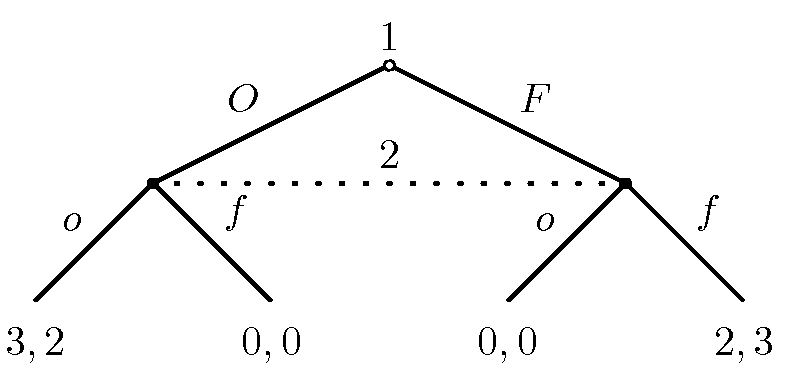 At the right are two versions of the battle of the sexes game, shown in extensive form. Below, the normal form for both of these games is shown as well.
The first game is simply sequential―when player 2 makes a choice, both parties are already aware of whether player 1 has chosen or .
The second game is also sequential, but the dotted line shows player 2's information set. This is the common way to show that when player 2 moves, he or she is not aware of what player 1 did.
This difference also leads to different predictions for the two games. In the first game, player 1 has the upper hand. They know that they can choose safely because ''once player 2 knows'' that player 1 has chosen opera, player 2 would rather go along for and get 2 than choose and get 0. Formally, that's applying subgame perfection to solve the game.
In the second game, player 2 can't observe what player 1 did, so it might as well be a
At the right are two versions of the battle of the sexes game, shown in extensive form. Below, the normal form for both of these games is shown as well.
The first game is simply sequential―when player 2 makes a choice, both parties are already aware of whether player 1 has chosen or .
The second game is also sequential, but the dotted line shows player 2's information set. This is the common way to show that when player 2 moves, he or she is not aware of what player 1 did.
This difference also leads to different predictions for the two games. In the first game, player 1 has the upper hand. They know that they can choose safely because ''once player 2 knows'' that player 1 has chosen opera, player 2 would rather go along for and get 2 than choose and get 0. Formally, that's applying subgame perfection to solve the game.
In the second game, player 2 can't observe what player 1 did, so it might as well be a
game theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed ...
, an information set is the basis for decision making in a game, which includes the actions available to players and the potential outcomes of each action. It consists of a collection of decision nodes that a player cannot distinguish between when making a move, due to incomplete information about previous actions or the current state of the game
A game is a structured type of play usually undertaken for entertainment or fun, and sometimes used as an educational tool. Many games are also considered to be work (such as professional players of spectator sports or video games) or art ...
. In other words, when a player's turn comes, they may be uncertain about which exact node in the game tree they are currently at, and the information set represents all the possibilities they must consider. Information sets are a fundamental concept particularly important in games with imperfect information
The imperfect ( abbreviated ) is a verb form that combines past tense (reference to a past time) and imperfective aspect (reference to a continuing or repeated event or state). It can have meanings similar to the English "was doing (something)" o ...
.
perfect information
Perfect information is a concept in game theory and economics that describes a situation where all players in a game or all participants in a market have knowledge of all relevant information in the system. This is different than complete informat ...
(such as chess
Chess is a board game for two players. It is an abstract strategy game that involves Perfect information, no hidden information and no elements of game of chance, chance. It is played on a square chessboard, board consisting of 64 squares arran ...
or Go), every information set contains exactly one decision node, as each player can observe all previous moves and knows the exact game state. However, in games with imperfect information—such as most card games
A card game is any game that uses playing cards as the primary device with which the game is played, whether the cards are of a traditional design or specifically created for the game (proprietary). Countless card games exist, including famil ...
like poker
Poker is a family of Card game#Comparing games, comparing card games in which Card player, players betting (poker), wager over which poker hand, hand is best according to that specific game's rules. It is played worldwide, with varying rules i ...
or bridge
A bridge is a structure built to Span (engineering), span a physical obstacle (such as a body of water, valley, road, or railway) without blocking the path underneath. It is constructed for the purpose of providing passage over the obstacle, whi ...
—information sets may contain multiple nodes, reflecting the player's uncertainty about the true state of the game. This uncertainty fundamentally changes how players must reason about optimal strategies.
The concept of information set was introduced by John von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, in ...
, motivated by his study of poker, and is now essential to the analysis of sequential games and the development of solution concepts such as subgame perfect equilibrium and perfect Bayesian equilibrium
In game theory, a Bayesian game is a strategic decision-making model which assumes players have incomplete information. Players may hold private information relevant to the game, meaning that the payoffs are not common knowledge. Bayesian games mo ...
.
In extensive form games
Information sets are primarily used in extensive form representations of games and are typically depicted in game trees. A game tree shows all possible paths from the start of a game to its various endings, with branches representing the choices available to players at each decision point. For games with imperfect information, the challenge lies in representing situations where a player cannot determine their exact position in the game. For example, in a card game, a player knows their own cards but not their opponent's cards, creating uncertainty about the true game state. This uncertainty is modeled using information sets. Information sets are typically represented in game trees using dotted lines connecting indistinguishable nodes, ovals encompassing multiple nodes, or similar notations indicating that a player cannot tell which of several positions they are actually in. This visual representation helps analyze how uncertainty affects optimal play.Formal definition
An information set in an extensive form game must satisfy the following properties: # Every node in the information set belongs to the same player. # The player cannot distinguish between any nodes within the same information set based on their available information. # All nodes in the same information set must have identical available actions. # No node in an information set can be an ancestor of another node in the same set (this would create a logical impossibility in the game timeline).Strategic implications
The structure of information sets profoundly affects strategic reasoning. When a player faces an information set with multiple nodes, they must formulate strategies that are optimal across all possible game states represented by that information set. This leads to several important game-theoretic concepts: *Mixed strategies
In game theory, a move, action, or play is any one of the options which a player can choose in a setting where the optimal outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the actio ...
often become necessary when facing uncertainty, as pure strategies might be exploitable by opponents who can predict them.
* Bayesian updating
Bayesian inference ( or ) is a method of statistical inference in which Bayes' theorem is used to calculate a probability of a hypothesis, given prior evidence, and update it as more information becomes available. Fundamentally, Bayesian inferen ...
occurs as players update their beliefs about which node in an information set they are at based on observed actions.
* Signaling and information revelation become strategic considerations, as players may take actions specifically to reveal or conceal information.
Dynamic games and backward induction
In games with multiple information sets, the strategic interaction becomes dynamic rather than static. Players must reason not just about current decisions but about future information sets that might arise. The standard solution technique for such games isbackward induction
Backward induction is the process of determining a sequence of optimal choices by reasoning from the endpoint of a problem or situation back to its beginning using individual events or actions. Backward induction involves examining the final point ...
, where players reason from the end of the game toward the beginning. For example, when player A chooses first, player B will make the best decision for themselves based on A's choice and their own information set at that time. Player A, anticipating this reaction, makes their initial choice to maximize their own payoff.
This sequential reasoning process is complicated in games with imperfect information, requiring more sophisticated solution concepts like sequential equilibrium that account for beliefs about which node in an information set a player is actually at.Example

 At the right are two versions of the battle of the sexes game, shown in extensive form. Below, the normal form for both of these games is shown as well.
The first game is simply sequential―when player 2 makes a choice, both parties are already aware of whether player 1 has chosen or .
The second game is also sequential, but the dotted line shows player 2's information set. This is the common way to show that when player 2 moves, he or she is not aware of what player 1 did.
This difference also leads to different predictions for the two games. In the first game, player 1 has the upper hand. They know that they can choose safely because ''once player 2 knows'' that player 1 has chosen opera, player 2 would rather go along for and get 2 than choose and get 0. Formally, that's applying subgame perfection to solve the game.
In the second game, player 2 can't observe what player 1 did, so it might as well be a
At the right are two versions of the battle of the sexes game, shown in extensive form. Below, the normal form for both of these games is shown as well.
The first game is simply sequential―when player 2 makes a choice, both parties are already aware of whether player 1 has chosen or .
The second game is also sequential, but the dotted line shows player 2's information set. This is the common way to show that when player 2 moves, he or she is not aware of what player 1 did.
This difference also leads to different predictions for the two games. In the first game, player 1 has the upper hand. They know that they can choose safely because ''once player 2 knows'' that player 1 has chosen opera, player 2 would rather go along for and get 2 than choose and get 0. Formally, that's applying subgame perfection to solve the game.
In the second game, player 2 can't observe what player 1 did, so it might as well be a simultaneous game
In game theory, a simultaneous game or static game is a game where each player chooses their action without knowledge of the actions chosen by other players. Simultaneous games contrast with sequential games, which are played by the players taki ...
. So subgame perfection doesn't get us anything that Nash equilibrium
In game theory, the Nash equilibrium is the most commonly used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player could gain by changing their own strategy (holding all other players' strategies fixed) ...
can't get us, and we have the standard 3 possible equilibria:
# Both choose opera
# both choose football
# or both use a mixed strategy
In game theory, a move, action, or play is any one of the options which a player can choose in a setting where the optimal outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the actio ...
, with player 1 choosing O(pera) 3/5 of the time and choosing football 2/5 of the time, and player 2 choosing 3/5 of the time and opera 2/5 of the time
See also
*Self-confirming equilibrium
In game theory, self-confirming equilibrium is a generalization of Nash equilibrium
In game theory, the Nash equilibrium is the most commonly used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player c ...
References
Further reading
* {{DEFAULTSORT:Information Set (Game Theory) Game theory