Incremental Deformations on:
[Wikipedia]
[Google]
[Amazon]
In
 Let be a three-dimensional
Let be a three-dimensional
 The Stroh formalism provides an optimal form to solve a great variety of elastic problems. Optimal means that one can construct an efficient numerical procedure to solve the incremental problem. By solving the incremental boundary value problem, one finds the relations among the material and geometrical parameters of the problem and the perturbation modes by which the wave propagates in the material, i.e. what denotes the instability. Everything depends on , the selected parameter denoted as the control one.
By this analysis, in a graph perturbation mode vs control parameter, the minimum value of the perturbation mode represents the first mode at which one can see the onset of the instability. For instance, in the picture, the first value of the mode in which the instability emerges is around since the trivial solution and does not have to be considered.
The Stroh formalism provides an optimal form to solve a great variety of elastic problems. Optimal means that one can construct an efficient numerical procedure to solve the incremental problem. By solving the incremental boundary value problem, one finds the relations among the material and geometrical parameters of the problem and the perturbation modes by which the wave propagates in the material, i.e. what denotes the instability. Everything depends on , the selected parameter denoted as the control one.
By this analysis, in a graph perturbation mode vs control parameter, the minimum value of the perturbation mode represents the first mode at which one can see the onset of the instability. For instance, in the picture, the first value of the mode in which the instability emerges is around since the trivial solution and does not have to be considered.
solid mechanics
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and ...
, the linear stability
Stability may refer to:
Mathematics
* Stability theory, the study of the stability of solutions to differential equations and dynamical systems
** Asymptotic stability
** Linear stability
** Lyapunov stability
** Orbital stability
** Structural st ...
analysis of an elastic solution is studied using the method of incremental deformations superposed on finite deformations. The method of incremental deformation can be used to solve static, quasi-static and time-dependent problems. The governing equations of the motion are ones of the classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
, such as the conservation of mass
In physics and chemistry, the law of conservation of mass or principle of mass conservation states that for any system closed to all transfers of matter and energy, the mass of the system must remain constant over time, as the system's mass ca ...
and the balance of linear and angular momentum, which provide the equilibrium configuration of the material. The main corresponding mathematical framework is described in the main Raymond Ogden
Raymond William Ogden (born 19 September 1943) is a British applied mathematician. He is the George Sinclair Professor of Mathematics at the Department of Mathematics and Statistics of the University of Glasgow.
Education
Ogden earned his B ...
's book ''Non-linear elastic deformations'' and in Biot's book ''Mechanics of incremental deformations'', which is a collection of his main papers.
Nonlinear Elasticity
Kinematics and Mechanics
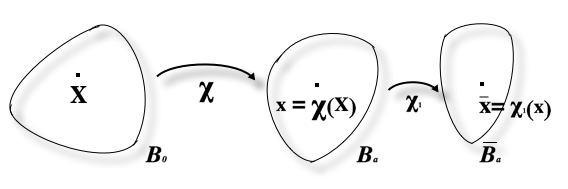
 Let be a three-dimensional
Let be a three-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean sp ...
. Let be two regions occupied by the material in two different instants of time. Let be the deformation
Deformation can refer to:
* Deformation (engineering), changes in an object's shape or form due to the application of a force or forces.
** Deformation (physics), such changes considered and analyzed as displacements of continuum bodies.
* Defo ...
which transforms the tissue from , i.e. the material/reference configuration, to the loaded configuration , i.e. current configuration. Let be a -diffeomorphism from to , with being the current position vector, given as a function of the material position . The deformation gradient is given by
Considering a hyperelastic material
A hyperelastic or Green elastic materialR.W. Ogden, 1984, ''Non-Linear Elastic Deformations'', , Dover. is a type of constitutive model for ideally elastic material for which the stress–strain relationship derives from a strain energy density ...
with an elastic strain energy density , the Piola-Kirchhoff stress tensor
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elonga ...
is given by .
For a quasi-static problem, without body force
In physics, a body force is a force that acts throughout the volume of a body.
Springer site - Book 'Solid mechanics'preview paragraph 'Body forces'./ref>
Forces due to gravity, electric fields and magnetic fields are examples of body forces. ...
s, the equilibrium equation is
:
where is the divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of t ...
with respect to the material coordinates.
If the material is incompressible, i.e. the volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). Th ...
of every subdomains does not change during the deformation, a Lagrangian multiplier is typically introduced to enforce the internal isochoric constraint . So that, the expression of the Piola stress tensor becomes
:
Boundary conditions
Let be the boundary of , the reference configuration, and , the boundary of , the current configuration. One defines the subset of on which Dirichlet conditions are applied, while Neumann conditions hold on , such that . If is the displacement vector to be assigned at the portion and is the traction vector to be assigned to the portion , the boundary conditions can be written in mixed-form, such as : where is the displacement and the vector is the unit outward normal to .Basic solution
The defined problem is called the boundary value problem ( BVP). Hence, let be a solution of the BVP. Since depends nonlinearly on the deformation gradient, this solution is generally not unique, and it depends on geometrical and material parameters of the problem. So, one has to employ the method of incremental deformation in order to highlight the existence of an adjacent solution for a critical value of a dimensionless parameter, called control parameter which "controls" the onset of the instability. This means that by increasing the value of this parameter, at a certain point new solutions appear. Hence, the selected basic solution is not anymore the stable one but it becomes unstable. In a physical way, at a certain time the stored energy, such as the integral of the density over all the domain of the basic solution is bigger than the one of the new solutions. To restore the equilibrium, the configuration of the material moves to another configuration which has lower energy.Method of incremental deformations superposed on finite deformations
To improve this method, one has to superpose a small displacement on the finite deformation basic solution . So that: :, where is the perturbed position and maps the basic position vector in the perturbed configuration . In the following, the incremental variables are indicated by , while the perturbed ones are indicated by .Deformation gradient
The perturbeddeformation gradient
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strai ...
is given by:
:,
where , where is the gradient operator with respect to the current configuration.
Stresses
The perturbed Piola stress is given by: : where denotes the contraction between two tensors, a forth-order tensor and a second-order tensor . Since depends on through , its expression can be rewritten by emphasizing this dependence, such as If the material isincompressible
In fluid mechanics or more generally continuum mechanics, incompressible flow ( isochoric flow) refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An ...
, one gets
where is the increment in and is called the elastic moduli associated to the pairs .
It is useful to derive the push-forward of the perturbed Piola stress be defined as
:
where is also known as ''the tensor of instantaneous moduli'', whose components are:
:.
Incremental governing equations
Expanding the equilibrium equation around the basic solution, one gets : Since is the solution to the equation at the zero-order, the incremental equation can be rewritten as : where is the divergence operator with respect to the actual configuration. The incremental incompressibility constraint reads : Expanding this equation around the basic solution, as before, one gets :Incremental boundary conditions
Let and be the prescribed increment of and respectively. Hence, the perturbed boundary condition are : where is the incremental displacement and .Solution of the incremental problem
The incremental equations represent the incremental boundary value problem (BVP) and define a system ofpartial differential equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
The function is often thought of as an "unknown" to be solved for, similarly to ...
s (PDEs). The unknowns of the problem depend on the considered case. For the first one, such as the compressible case, there are three unknowns, such as the components of the incremental deformations , linked to the perturbed deformation by this relation . For the latter case, instead, one has to take into account also the increment of the Lagrange multiplier , introduced to impose the isochoric constraint.
The main difficulty to solve this problem is to transform the problem in a more suitable form for implementing an efficient and robusted numerical solution procedure. The one used in this area is the Stroh formalism. It was originally developed by Stroh for a steady state elastic problem and allows the set of four PDEs with the associated boundary conditions to be transformed into a set of ODEs of first order
In mathematics and other formal sciences, first-order or first order most often means either:
* "linear" (a polynomial of degree at most one), as in first-order approximation and other calculus uses, where it is contrasted with "polynomials of hig ...
with initial conditions. The number of equations depends on the dimension of the space in which the problem is set. To do this, one has to apply variable separation and assume periodicity in a given direction depending on the considered situation. In particular cases, the system can be rewritten in a compact form by using the Stroh formalism. Indeed, the shape of the system looks like
where is the vector which contains all the unknowns of the problem, is the only variable on which the rewritten problem depends and the matrix is so-called ''Stroh'' matrix and it has the following form
:
where each block is a matrix and its dimension depends on the dimension of the problem. Moreover, a crucial property of this approach is that , i.e. is the hermitian matrix of .
Conclusion and remark
See also
*Deformation (mechanics)
In physics, deformation is the continuum mechanics transformation of a body from a ''reference'' configuration to a ''current'' configuration. A configuration is a set containing the positions of all particles of the body.
A deformation can ...
*Elastic instability
Elastic instability is a form of instability occurring in elastic systems, such as buckling of beams and plates subject to large compressive loads.
There are a lot of ways to study this kind of instability. One of them is to use the method of inc ...
*Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such ...
References
{{Reflist Elasticity (physics)