Hurwitz Integer

In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are ''either'' all integers ''or'' all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz quaternions is

:$H = \left\.$

That is, either ''a'', ''b'', ''c'', ''d'' are all integers, or they are all half-integers.
''H'' is closed under quaternion multiplication and addition, which makes it a subring of the ring of all quaternions H. Hurwitz quaternions were introduced by .

A Lipschitz quaternion (or Lipschitz integer) is a quaternion whose components are all integers. The set of all Lipschitz quaternions

:$L = \left\$

forms a subring of the Hurwitz quaternions ''H''. Hurwitz integers have the advantage over Lipschitz integers that it is possible to perform Euclidean division on them, obtaining a small remainder.

Both the Hurwitz and Lipschitz quaternions are examples of noncommutative domains which are not division rings.

Structure of the ring of Hurwitz quaternions

As an additive group, ''H'' is free abelian with generators It therefore forms a lattice in R⁴. This lattice is known as the ''F''₄ lattice since it is the root lattice of the semisimple Lie algebra ''F''₄. The Lipschitz quaternions ''L'' form an index 2 sublattice of ''H''.

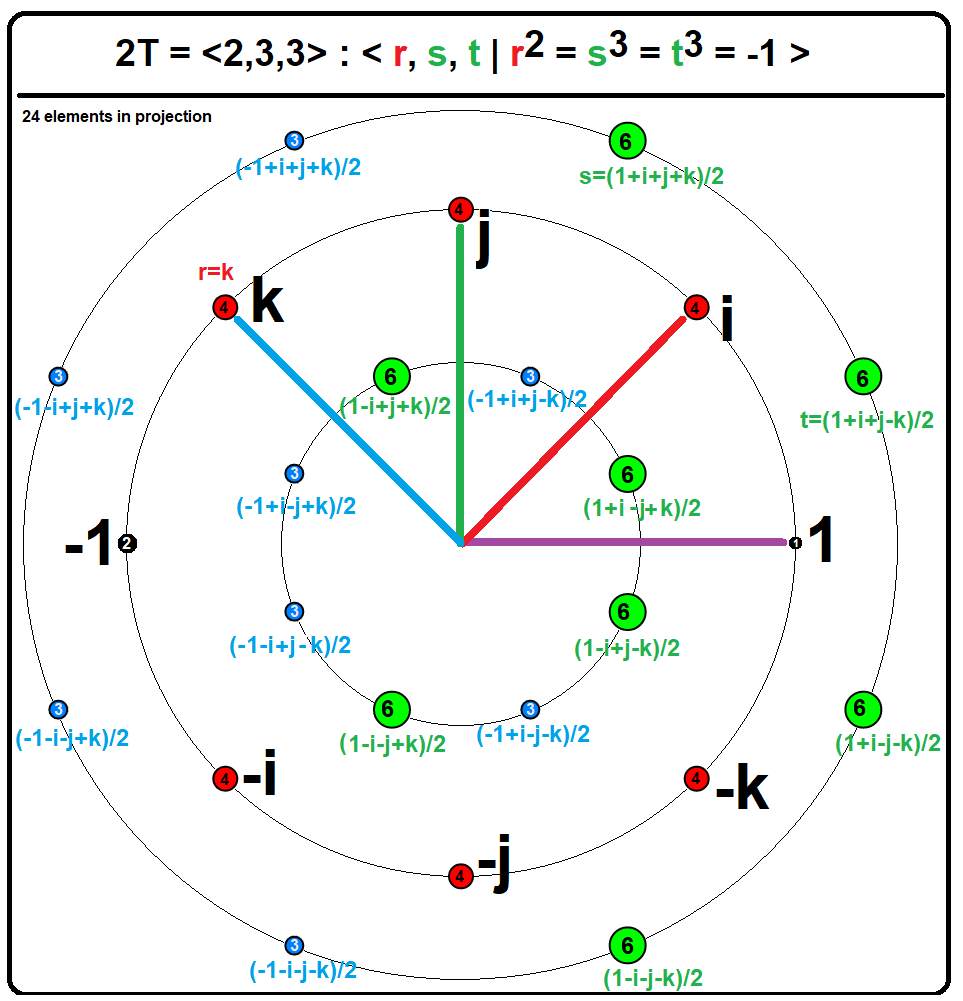
The group of units in ''L'' is the order 8 quaternion group The group of units in ''H'' is a nonabelian group of order 24 known as the binary tetrahedral group. The elements of this group include the 8 elements of ''Q'' along with the 16 quaternions where signs may be taken in any combination. The quaternion group is a normal subgroup of the binary tetrahedral group U(''H''). The elements of U(''H''), which all have norm 1, form the vertices of the 24-cell inscribed in the 3-sphere.

The Hurwitz quaternions form an order (in the sense of ring theory) in the division ring of quaternions with rational components. It is in fact a maximal order; this accounts for its importance. The Lipschitz quaternions, which are the more obvious candidate for the idea of an ''integral quaternion'', also form an order. However, this latter order is not a maximal one, and therefore (as it turns out) less suitable for developing a theory of left ideals comparable to that of algebraic number theory. What Adolf Hurwitz realised, therefore, was that this definition of Hurwitz integral quaternion is the better one to operate with. For a non-commutative ring such as H, maximal orders need not be unique, so one needs to fix a maximal order, in carrying over the concept of an algebraic integer.

The lattice of Hurwitz quaternions

The (arithmetic, or field) norm of a Hurwitz quaternion , given by , is always an integer. By a theorem of Lagrange every nonnegative integer can be written as a sum of at most four squares. Thus, every nonnegative integer is the norm of some Lipschitz (or Hurwitz) quaternion. More precisely,
the number ''c''(''n'') of Hurwitz quaternions of given positive norm ''n'' is 24 times the sum of the odd divisors of ''n''. The generating function of the numbers ''c''(''n'') is given by the level 2 weight 2 modular form
:$2E_2(2\tau)-E_2(\tau) = \sum_nc(n)q^n = 1 + 24q + 24q^2 + 96q^3 + 24q^4 + 144q^5 + \dots$
where
:$q=e^$
and
:$E_2(\tau) = 1-24\sum_n\sigma_1(n)q^n$
is the weight 2 level 1 Eisenstein series (which is a quasimodular form) and ''σ''₁(''n'') is the sum of the divisors of ''n''.

Factorization into irreducible elements

A Hurwitz integer is called irreducible if it is not 0 or a unit and is not a product of non-units.
A Hurwitz integer is irreducible if and only if its norm is a prime number. The irreducible quaternions are sometimes called prime quaternions, but this can be misleading as they are not primes in the usual sense of commutative algebra: it is possible for an irreducible quaternion to divide a product ''ab'' without dividing either ''a'' or ''b''. Every Hurwitz quaternion can be factored as a product of irreducible quaternions. This factorization is not in general unique, even up to units and order, because a positive odd prime ''p'' can be written in 24(''p''+1) ways as a product of two irreducible Hurwitz quaternions of norm ''p'', and for large ''p'' these cannot all be equivalent under left and right multiplication by units as there are only 24 units. However, if one excludes this case then there is a version of unique factorization. More precisely, every Hurwitz quaternion can be written uniquely as the product of a positive integer and a primitive quaternion (a Hurwitz quaternion not divisible by any integer greater than 1). The factorization of a primitive quaternion into irreducibles is unique up to order and units in the following sense: if
:''p''₀''p''₁...''p''_''n''
and
:''q''₀''q''₁...''q''_''n''
are two factorizations of some primitive Hurwitz quaternion into irreducible quaternions where ''p''_''k'' has the same norm as ''q''_''k'' for all ''k'', then

: $\begin q_0 & = p_0 u_1 \\ q_1 & = u_1^ p_1 u_2 \\ & \,\,\,\vdots \\ q_n & = u_n^ p_n \end$
for some units ''u''_''k''.

Division with remainder

The ordinary integers and the Gaussian integers allow a division with remainder or Euclidean division.

For positive integers ''N'' and ''D'', there is always a quotient ''Q'' and a nonnegative remainder ''R'' such that
* ''N'' = ''QD'' + ''R'' where ''R'' < ''D''.
For complex or Gaussian integers ''N'' = ''a'' + i''b'' and ''D'' = ''c'' + i''d'', with the norm N(''D'') > 0, there always exist ''Q'' = ''p'' + i''q'' and ''R'' = ''r'' + i''s'' such that
* ''N'' = ''QD'' + ''R'', where N(''R'') < N(''D'').
However, for Lipschitz integers ''N'' = (''a'', ''b'', ''c'', ''d'') and ''D'' = (''e'', ''f'', ''g'', ''h'') it can happen that N(''R'') = N(''D''). This motivated a switch to Hurwitz integers, for which the condition N(''R'') < N(''D'') is guaranteed.

Many algorithms depend on division with remainder, for example, Euclid's algorithm for the greatest common divisor.

See also

* Gaussian integer
* Eisenstein integer
* The icosians
* The Lie group F₄
* The E₈ lattice

References

*
*{{cite book , first=Adolf , last=Hurwitz , title=Vorlesungen Über die Zahlentheorie der Quaternionen , url=https://books.google.com/books?id=4vKgBgAAQBAJ&pg=PP1 , date=2013 , orig-year=1919 , publisher=Springer-Verlag , isbn=978-3-642-47536-8 , jfm=47.0106.01 , ref={{harvid, Hurwitz, 1919

Quaternions