Huber loss on:
[Wikipedia]
[Google]
[Amazon]
In
 The Huber loss function describes the penalty incurred by an estimation procedure . Huber (1964) defines the loss function piecewise by
This function is quadratic for small values of , and linear for large values, with equal values and slopes of the different sections at the two points where . The variable often refers to the residuals, that is to the difference between the observed and predicted values , so the former can be expanded to
The Huber loss is the
The Huber loss function describes the penalty incurred by an estimation procedure . Huber (1964) defines the loss function piecewise by
This function is quadratic for small values of , and linear for large values, with equal values and slopes of the different sections at the two points where . The variable often refers to the residuals, that is to the difference between the observed and predicted values , so the former can be expanded to
The Huber loss is the 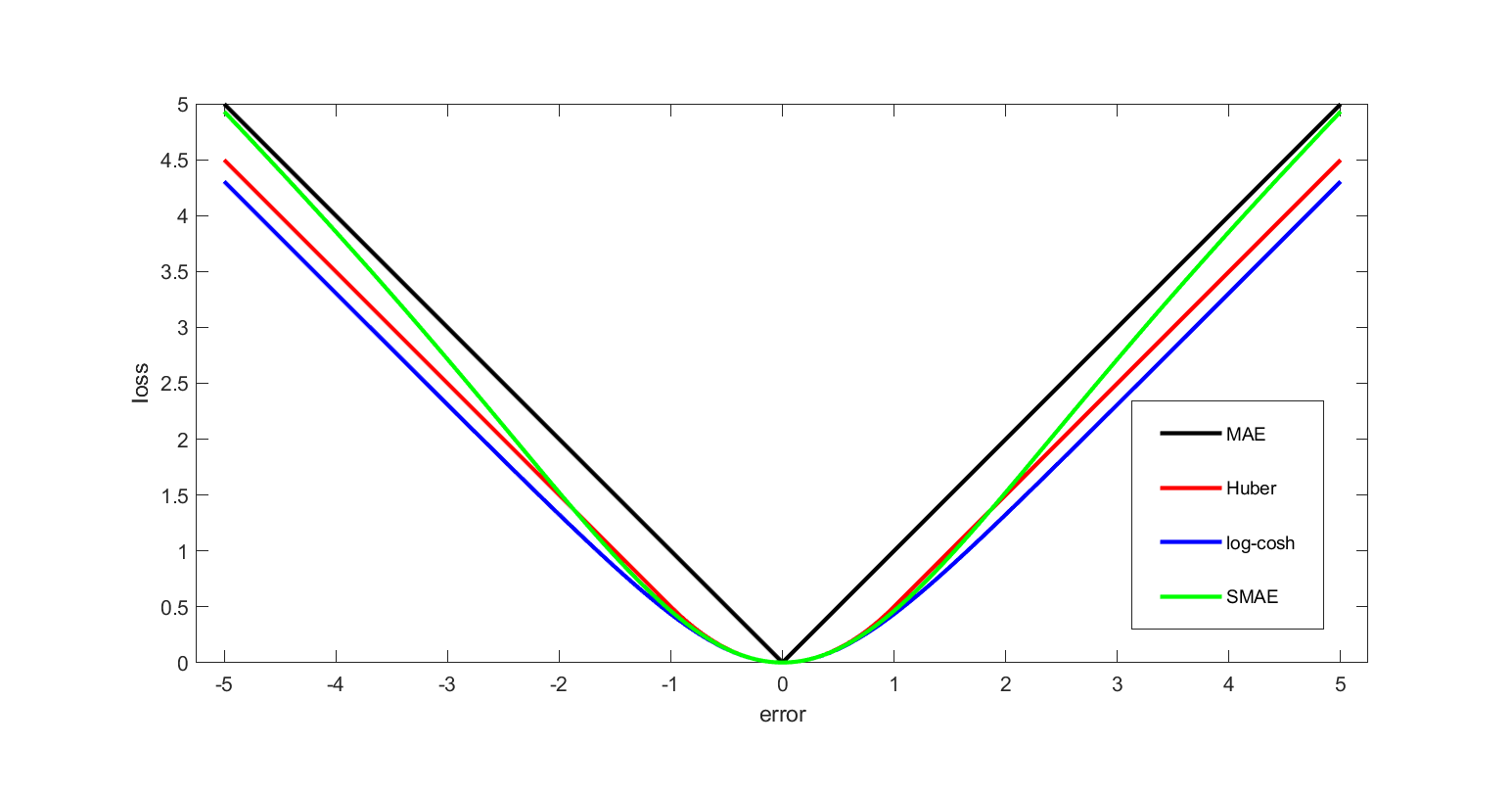
statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, the Huber loss is a loss function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost ...
used in robust regression
In robust statistics, robust regression seeks to overcome some limitations of traditional regression analysis. A regression analysis models the relationship between one or more independent variables and a dependent variable. Standard types of re ...
, that is less sensitive to outlier
In statistics, an outlier is a data point that differs significantly from other observations. An outlier may be due to a variability in the measurement, an indication of novel data, or it may be the result of experimental error; the latter are ...
s in data than the squared error loss. A variant for classification is also sometimes used.
Definition
convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...
of the absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
function with the rectangular function
The rectangular function (also known as the rectangle function, rect function, Pi function, Heaviside Pi function, gate function, unit pulse, or the normalized boxcar function) is defined as
\operatorname\left(\frac\right) = \Pi\left(\frac\ri ...
, scaled and translated. Thus it "smoothens out" the former's corner at the origin.

Motivation
Two very commonly used loss functions are the squared loss, , and the absolute loss, . The squared loss function results in anarithmetic mean
In mathematics and statistics, the arithmetic mean ( ), arithmetic average, or just the ''mean'' or ''average'' is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results fr ...
-unbiased estimator
In statistics, the bias of an estimator (or bias function) is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called ''unbiased''. In stat ...
, and the absolute-value loss function results in a median
The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “ ...
-unbiased estimator (in the one-dimensional case, and a geometric median
In geometry, the geometric median of a discrete point set in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances or absolute ...
-unbiased estimator for the multi-dimensional case). The squared loss has the disadvantage that it has the tendency to be dominated by outliers—when summing over a set of 's (as in ), the sample mean is influenced too much by a few particularly large -values when the distribution is heavy tailed: in terms of estimation theory
Estimation theory is a branch of statistics that deals with estimating the values of Statistical parameter, parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such ...
, the asymptotic relative efficiency of the mean is poor for heavy-tailed distributions.
As defined above, the Huber loss function is strongly convex in a uniform neighborhood of its minimum ; at the boundary of this uniform neighborhood, the Huber loss function has a differentiable extension to an affine function at points and . These properties allow it to combine much of the sensitivity of the mean-unbiased, minimum-variance estimator of the mean (using the quadratic loss function) and the robustness of the median-unbiased estimator (using the absolute value function).
Pseudo-Huber loss function
The Pseudo-Huber loss function can be used as a smooth approximation of the Huber loss function. It combines the best properties of L2 squared loss and L1 absolute loss by being strongly convex when close to the target/minimum and less steep for extreme values. The scale at which the Pseudo-Huber loss function transitions from L2 loss for values close to the minimum to L1 loss for extreme values and the steepness at extreme values can be controlled by the value. The Pseudo-Huber loss function ensures that derivatives are continuous for all degrees. It is defined as As such, this function approximates for small values of , and approximates a straight line with slope for large values of . While the above is the most common form, other smooth approximations of the Huber loss function also exist.Variant for classification
Forclassification
Classification is the activity of assigning objects to some pre-existing classes or categories. This is distinct from the task of establishing the classes themselves (for example through cluster analysis). Examples include diagnostic tests, identif ...
purposes, a variant of the Huber loss called ''modified Huber'' is sometimes used. Given a prediction (a real-valued classifier score) and a true binary
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two values (0 and 1) for each digit
* Binary function, a function that takes two arguments
* Binary operation, a mathematical op ...
class label , the modified Huber loss is defined as
The term is the hinge loss
In machine learning, the hinge loss is a loss function used for training classifiers. The hinge loss is used for "maximum-margin" classification, most notably for support vector machines (SVMs).
For an intended output and a classifier score , ...
used by support vector machine
In machine learning, support vector machines (SVMs, also support vector networks) are supervised max-margin models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laborato ...
s; the quadratically smoothed hinge loss is a generalization of .
Applications
The Huber loss function is used inrobust statistics
Robust statistics are statistics that maintain their properties even if the underlying distributional assumptions are incorrect. Robust Statistics, statistical methods have been developed for many common problems, such as estimating location parame ...
, M-estimation and additive model
In statistics, an additive model (AM) is a nonparametric regression method. It was suggested by Jerome H. Friedman and Werner Stuetzle (1981) and is an essential part of the ACE algorithm. The ''AM'' uses a one-dimensional smoother to build a ...
ling.
See also
* Winsorizing *Robust regression
In robust statistics, robust regression seeks to overcome some limitations of traditional regression analysis. A regression analysis models the relationship between one or more independent variables and a dependent variable. Standard types of re ...
* M-estimator
In statistics, M-estimators are a broad class of extremum estimators for which the objective function is a sample average. Both non-linear least squares and maximum likelihood estimation are special cases of M-estimators. The definition of M-estim ...
* Visual comparison of different M-estimators
References
{{DEFAULTSORT:Huber Loss Function Robust statistics M-estimators Loss functions