Honeycomb Conjecture

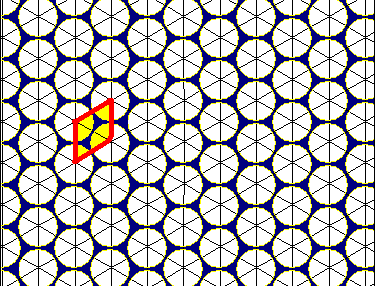The honeycomb theorem, formerly the honeycomb conjecture, states that a regular hexagonal grid or honeycomb has the least total perimeter of any subdivision of the plane into regions of equal area. The conjecture was proven in 1999 by mathematician Thomas C. Hales.

Theorem

Let $\Gamma$ be any system of smooth curves in $\mathbb^2$, subdividing the plane into regions (connected components of the complement of $\Gamma$) all of which are bounded and have unit area. Then, averaged over large disks in the plane, the average length of $\Gamma$ per unit area is at least as large as for the hexagon tiling. The theorem applies even if the complement of $\Gamma$ has additional components that are unbounded or whose area is not one; allowing these additional components cannot shorten $\Gamma$. Formally, let $B(0,r)$ denote the disk of radius $r$ centered at the origin, let $L_r$ denote the total length of $\Gamma\cap B(0,r)$, and let $A_r$ denote the total area of $B(0,r)$ covered by bounded unit-area components. (If these are the only components, then $A_r=\pi r^2$.) Then the theorem states that
\limsup_ \frac\ge\sqrt
The value on the right hand side of the inequality is the limiting length per unit area of the hexagonal tiling.

History

The first record of the conjecture dates back to 36 BC, from Marcus Terentius Varro, but is often attributed to Pappus of Alexandria ().
In the 17th century, Jan Brożek used a similar theorem to argue why bees create hexagonal honeycombs. In 1943, László Fejes Tóth published a proof for a special case of the conjecture, in which each cell is required to be a convex polygon. The full conjecture was proven in 1999 by mathematician Thomas C. Hales, who mentions in his work that there is reason to believe that the conjecture may have been present in the minds of mathematicians before Varro.

It is also related to the densest circle packing of the plane, in which every circle is tangent to six other circles, which fill just over 90% of the area of the plane.

The case when the problem is restricted to a square grid was solved in 1989 by Jaigyoung Choe who proved that the optimal figure is an irregular hexagon.

See also

*Weaire–Phelan structure, a counter-example to the ''Kelvin conjecture'' on the solution of the similar problem in 3D.

References

{{reflist

Discrete geometry
Euclidean plane geometry
Conjectures that have been proved