Hjelmslev transformation

In mathematics, the Hjelmslev transformation is an effective method for mapping an entire hyperbolic plane into a circle with a finite radius. The transformation was invented by Danish mathematician Johannes Hjelmslev. It utilizes Nikolai Ivanovich Lobachevsky's 23rd theorem from his work Geometrical Investigations on the Theory of Parallels.

Lobachevsky observes, using a combination of his 16th and 23rd theorems, that it is a fundamental characteristic of hyperbolic geometry that there must exist a distinct angle of parallelism for any given line length. Let us say for the length AE, its angle of parallelism is angle BAF. This being the case, line AH and EJ will be hyperparallel, and therefore will never meet. Consequently, any line drawn perpendicular to base AE between A and E must necessarily cross line AH at some finite distance. Johannes Hjelmslev discovered from this a method of compressing an entire hyperbolic plane into a finite circle.

Construction

Formalisation

The Hjelmslev transformation is a function designated as $H(P)$ which operates upon all points $P_n$ in hyperbolic (Lobachevskian) space. Given an angle $\alpha$ such that $0 < \alpha < \frac$, and an origin $O$, this mapping yields images $P'_n$ where the following properties are preserved:

# The image of a circle with a center at $O$ is a circle with a center at $O$.
# The image of a rectilinear angle is a rectilinear angle.
# Any angle with vertex $O$ is mapped onto itself, i.e. any angle with vertex $O$ is preserved.
# The image of a right angle with one side passing through $O$ is a right angle with one side passing through $O$.
# The image of any straight line will be a finite straight line segment.
# Finally, the point order is maintained throughout a transformation, i.e. if B is between A and C, the image of B will be between the image of A and the image of C.

This function is useful in the studies of hyperbolic (Lobachevskian) space because it produces characteristic figures of parallel lines. Given a set of two parallel lines $\overline$, $\overline$ such that $\overline \parallel \overline$, the resulting images $\overline$, $\overline$ will form a triangle $\triangle A'B'IC'D'$ with an imaginary vertex $I$ in their direction of parallelism.

Transformation of a single point $P$ into image $P'$

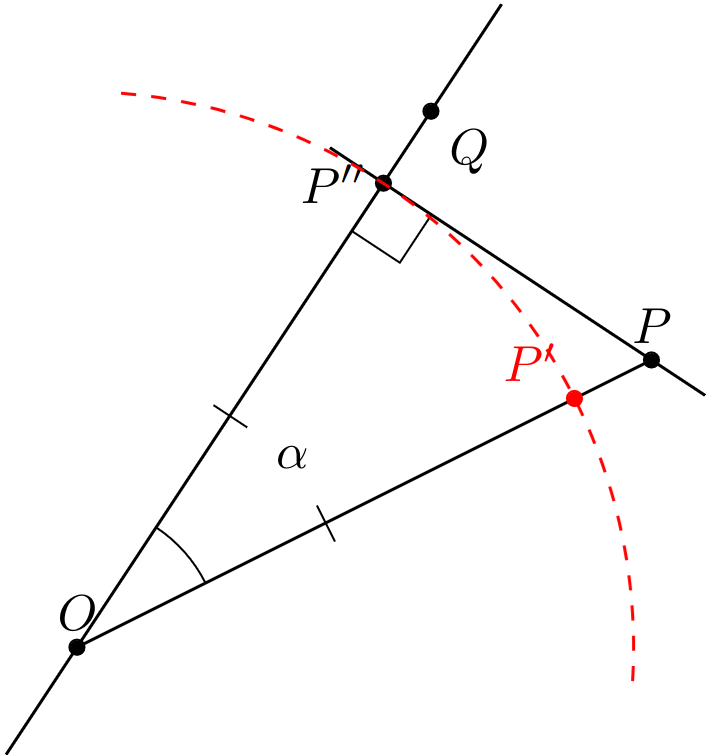
Given $\alpha$, $O$, $P$, in order to find the $P'$ (image) of $P$. First draw the line segment $\overline$, connecting the point $P$ to the origin $O$. Next, construct an auxiliary line $\overline$ such that $\angle POQ = \alpha$. Point $Q$ is only necessary to define the line $\overline$.

Now construct the perpendicular line $\overline$ passing through the point $P$, perpendicular to $\overline$. This will form the right angle $\angle OP''P$ at point $P''$:

Using line segment $\overline$ as a radius, construct a circle with center $O$ such that the circumference of said circle intersects $\overline$ at a point $\color P'$. Thus, we obtain the point $\color P'$ on line segment $OP$, which is the Hjelmslev transformation $H(P)$ of the given point $P$. $H(P) = \color P'$:

The Hjelmslev Disk

Let $\overline$ be parallel to $\overline$, where $\angle P_3 P_1 P_2$ is the angle of parallelism. By performing the transformation for every point on the two parallel lines, we yield the Hjelmslev circle:

The circumference of the circle created does not have a corresponding location within the plane, and therefore, the product of a Hjelmslev transformation is more aptly called a Hjelmslev Disk. Likewise, when this transformation is extended in all three dimensions, it is referred to as a Hjelmslev Ball.

The Hjelmslev transformation and the Klein model

If we represent hyperbolic space by means of the Klein model, and take the center of the Hjelmslev transformation to be the center point of the Klein model, then the Hjelmslev transformation maps points in the unit disk to points in a disk centered at the origin with a radius less than one. Given a real number k, the Hjelmslev transformation, if we ignore rotations, is in effect what we obtain by mapping a vector u representing a point in the Klein model to
ku, with 0uniform scaling which sends lines to lines and so forth. To beings living in a hyperbolic space it might be a suitable way of making a map.

See also

* Hjelmslev's theorem

References

{{DEFAULTSORT:Hjelmslev Transformation
Hyperbolic geometry