History Of Mathematical Notation on:
[Wikipedia]
[Google]
[Amazon]
The history of mathematical notation covers the introduction, development, and cultural diffusion of
 Written mathematics began with numbers expressed as
Written mathematics began with numbers expressed as
 The ancient Greeks made steps in the abstraction of geometry. Euclid's ''Elements'' (c. 300 BC) is the earliest extant documentation of the axioms of plane geometry—though Proclus tells of an earlier axiomatisation by
The ancient Greeks made steps in the abstraction of geometry. Euclid's ''Elements'' (c. 300 BC) is the earliest extant documentation of the axioms of plane geometry—though Proclus tells of an earlier axiomatisation by
14
/ref> which was based on the system of the Egyptians and was later adapted and used by the Romans. Greek numerals one through four were written as vertical lines, as in the hieroglyphics. The symbol for five was the Greek letter Π (pi), representing the Greek word for 'five' (''pente''). Numbers six through nine were written as a Π with vertical lines beside it. Ten was represented by the letter Δ (delta), from word for 'ten' (''deka''), one hundred by the letter from the word for hundred, and so on. This system was 'acrophonic' since it was based on the first sound of the numeral. Milesian (Ionian) numeration was another Greek numeral system. It was constructed by partitioning the twenty-four letters of the Greek alphabet, plus three archaic letters, into three classes of nine letters each, and using them to represent the units, tens, and hundreds. (
683
/ref> and could be used with tolerable effect as an instrument of calculation, to which purpose the Roman system was totally inapplicable. Greek mathematical reasoning was almost entirely geometric (albeit often used to reason about non-geometric subjects such as
 The ancient Chinese used numerals that look much like the tally system. Numbers one through four were horizontal lines. Five was an X between two horizontal lines; it looked almost exactly the same as the
The ancient Chinese used numerals that look much like the tally system. Numbers one through four were horizontal lines. Five was an X between two horizontal lines; it looked almost exactly the same as the  Early Chinese mathematical inventions include a place value system known as
Early Chinese mathematical inventions include a place value system known as
ImageSize = width:678 height:285
PlotArea = left:65 right:55 bottom:20 top:15
AlignBars = justify
Colors =
id:time value:rgb(0.7,0.7,1) #
id:period value:rgb(1,0.7,0.5) #
id:age value:rgb(0.95,0.85,0.5) #
id:era value:rgb(1,0.85,0.5) #
id:eon value:rgb(1,0.85,0.7) #
id:filler value:gray(0.8) # background bar
id:black value:black
Period = from:1360 till:1962
TimeAxis = orientation:horizontal
ScaleMajor = unit:year increment:100 start:1360
ScaleMinor = unit:year increment:10 start:1360
PlotData =
align:center textcolor:black fontsize:8 mark:(line,black) width:15
bar: color:filler width:15
from:1360 till:1962 shift:(0,10) text: Symbolic Notation
from:1360 till:1704 shift:(-40,0) text:Early
from:1704 till:1876 text:High
from:1876 till:1962 text:Late
bar: color:age width:5
from:1360 till:1618 shift:(0,-10) text:Arithmetic
from:1618 till:1718 shift:(0,-10) text:Multiplication
from:1718 till:1846 shift:(0,-10) text:Division
from:1846 till:1962 shift:(10,-10) text:Abstraction
mark:(line,black) textcolor:black fontsize:M
bar:Events color:filler align:left
at:1360 shift:(2,0) text:" plus"
at:1489 shift:(0,6) text:"
 The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. The two most widely used arithmetic symbols are addition and subtraction, + and −. The
The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. The two most widely used arithmetic symbols are addition and subtraction, + and −. The
 In 1864 James Clerk Maxwell reduced all of the then-current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in ''A Dynamical Theory of the Electromagnetic Field''. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.) (See Maxwell's equations.) The method of calculation that is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used, they are known as Lagrange's equations. In 1871 Richard Dedekind defined a field (mathematics), field to be a set of real or complex numbers which is closed under the four arithmetic operations. In 1873 Maxwell presented ''A Treatise on Electricity and Magnetism''.
In 1878 William Kingdon Clifford published his ''Elements of Dynamic''. Clifford developed split-biquaternions (e.g. History of quaternions, ) which he called ''algebraic motors''. Clifford obviated quaternion study by separating the
In 1864 James Clerk Maxwell reduced all of the then-current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in ''A Dynamical Theory of the Electromagnetic Field''. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.) (See Maxwell's equations.) The method of calculation that is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used, they are known as Lagrange's equations. In 1871 Richard Dedekind defined a field (mathematics), field to be a set of real or complex numbers which is closed under the four arithmetic operations. In 1873 Maxwell presented ''A Treatise on Electricity and Magnetism''.
In 1878 William Kingdon Clifford published his ''Elements of Dynamic''. Clifford developed split-biquaternions (e.g. History of quaternions, ) which he called ''algebraic motors''. Clifford obviated quaternion study by separating the
 Albert Einstein, in 1916, introduced Einstein notation, which summed over a set of index notation, indexed terms in a formula, thus exerting notational brevity. For example, for indices ranging over the Set (mathematics), set ,
:
is reduced by convention to:
:
Albert Einstein, in 1916, introduced Einstein notation, which summed over a set of index notation, indexed terms in a formula, thus exerting notational brevity. For example, for indices ranging over the Set (mathematics), set ,
:
is reduced by convention to:
:
Upper indices are not Exponentiation, exponents but are indices of coordinates,
''Four Lectures on Relativity and Space''
Around 1924, Jan Arnoldus Schouten developed the modern notation and formalism for the Ricci calculus framework during the absolute differential calculus applications to general relativity and differential geometry in the early twentieth century. Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields. In 1925, Enrico Fermi described a Fermi–Dirac statistics, system comprising many identical particles that obey the Pauli exclusion principle, afterwards developing a diffusion equation (Fermi age equation). In 1926, Oskar Klein develop the Kaluza–Klein theory. In 1928, Emil Artin abstracted ring theory with Artinian rings. In 1933, Andrey Kolmogorov introduces the Kolmogorov axioms. In 1937, Bruno de Finetti deduced the "Coherence (philosophical gambling strategy), operational subjective" concept.
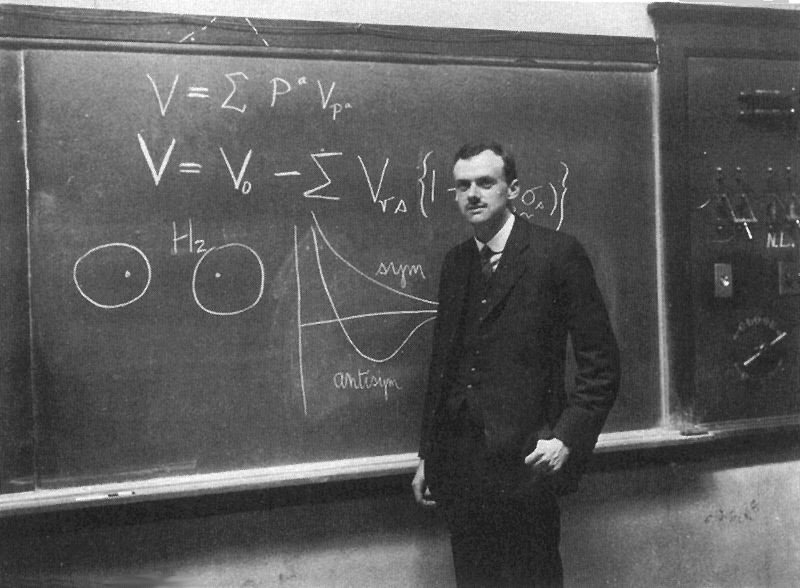 Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of bracket, angle brackets and vertical bars. It can also be used to denote abstract vector space, vectors and linear functionals. It is so called because the inner product (or
Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of bracket, angle brackets and vertical bars. It can also be used to denote abstract vector space, vectors and linear functionals. It is so called because the inner product (or
A Short Account of the History of Mathematics
By Walter William Rouse Ball.
A Primer of the History of Mathematics
By Walter William Rouse Ball.
A History of Elementary Mathematics
With Hints on Methods of Teaching. By Florian Cajori.
A History of Elementary Mathematics
By Florian Cajori.
A History of Mathematics
By Florian Cajori.
A Short History of Greek Mathematics
By James Gow (scholar), James Gow.
On the Development of Mathematical Thought During the Nineteenth Century
By John Theodore Merz.
A New Mathematical and Philosophical Dictionary
By Peter Barlow.
Historical Introduction to Mathematical Literature
By George Abram Miller
A Brief History of Mathematics
By Karl Fink, Wooster Woodruff Beman, David Eugene Smith
History of Modern Mathematics
By David Eugene Smith.
History of modern mathematics
By David Eugene Smith, Mansfield Merriman. ;Other * Principia Mathematica
Volume 1
Volume 2
By Alfred North Whitehead, Bertrand Russell.
The Mathematical Principles of Natural Philosophy
Volume 1, Issue 1. By Sir Isaac Newton, Andrew Motte, William Davis, John Machin, William Emerson.
General investigations of curved surfaces of 1827 and 1825
By Carl Friedrich Gaus.
Mathematical Notation: Past and Future
files.chem.vt.edu.
Some Common Mathematical Symbols and Abbreviations (with History)
Isaiah Lankham, Bruno Nachtergaele, Anne Schilling. {{History of mathematics History of mathematics, Mathematical notation Mathematical notation Articles which contain graphical timelines
mathematical symbol
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula ...
s and the conflicts between notational methods that arise during a notation's move to popularity or obsolescence. Mathematical notation
Mathematical notation consists of using glossary of mathematical symbols, symbols for representing operation (mathematics), operations, unspecified numbers, relation (mathematics), relations, and any other mathematical objects and assembling ...
comprises the symbols used to write mathematical equation
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for ...
s and formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwe ...
s. Notation generally implies a set of well-defined
In mathematics, a well-defined expression or unambiguous expression is an expression (mathematics), expression whose definition assigns it a unique interpretation or value. Otherwise, the expression is said to be ''not well defined'', ill defined ...
representations of quantities and symbols operators. The history includes Hindu–Arabic numerals, letters from the Roman
Roman or Romans most often refers to:
*Rome, the capital city of Italy
*Ancient Rome, Roman civilization from 8th century BC to 5th century AD
*Roman people, the people of Roman civilization
*Epistle to the Romans, shortened to Romans, a letter w ...
, Greek
Greek may refer to:
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group
*Greek language, a branch of the Indo-European language family
**Proto-Greek language, the assumed last common ancestor of all kno ...
, Hebrew
Hebrew (; ''ʿÎbrit'') is a Northwest Semitic languages, Northwest Semitic language within the Afroasiatic languages, Afroasiatic language family. A regional dialect of the Canaanite languages, it was natively spoken by the Israelites and ...
, and German alphabet
An alphabet is a standard set of letter (alphabet), letters written to represent particular sounds in a spoken language. Specifically, letters largely correspond to phonemes as the smallest sound segments that can distinguish one word from a ...
s, and a variety of symbols invented by mathematicians over the past several centuries.
The historical development of mathematical notation can be divided into three stages:
* ''Rhetorical
Rhetoric is the art of persuasion. It is one of the three ancient arts of discourse (trivium) along with grammar and logic/dialectic. As an academic discipline within the humanities, rhetoric aims to study the techniques that speakers or writ ...
stage''—where calculations are performed by words and tallies, and no symbols are used.
* ''Syncopated
In music, syncopation is a variety of rhythms played together to make a piece of music, making part or all of a tune or piece of music off-beat (music), off-beat. More simply, syncopation is "a disturbance or interruption of the regular flow of ...
stage''—where frequently-used operations and quantities are represented by symbolic syntactical abbreviations, such as letters or numerals. During antiquity and the medieval periods, bursts of mathematical creativity were often followed by centuries of stagnation. As the early modern age opened and the worldwide spread of knowledge began, written examples of mathematical developments came to light.
* ''Symbolic stage''—where comprehensive systems of notation supersede rhetoric. The increasing pace of new mathematical developments, interacting with new scientific discoveries, led to a robust and complete usage of symbols. This began with mathematicians of medieval India and mid-16th century Europe, and continues through the present day.
The more general area of study known as the history of mathematics
The history of mathematics deals with the origin of discoveries in mathematics and the History of mathematical notation, mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples ...
primarily investigates the origins of discoveries in mathematics. The specific focus of this article is the investigation of mathematical methods and notations of the past.
Rhetorical stage
Many areas of mathematics began with the study of real world problems, before the underlying rules and concepts were identified and defined asabstract structure
In mathematics and related fields, an abstract structure is a way of describing a set of mathematical objects and the relationships between them, focusing on the essential rules and properties rather than any specific meaning or example.{{Cite book ...
s. For example, geometry has its origins in the calculation of distances and area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-di ...
s in the real world; algebra started with methods of solving problems in arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
. The earliest mathematical notations emerged from these problems.
There can be no doubt that most early peoples who left records knew something of numeration and mechanics
Mechanics () is the area of physics concerned with the relationships between force, matter, and motion among Physical object, physical objects. Forces applied to objects may result in Displacement (vector), displacements, which are changes of ...
and that a few were also acquainted with the elements of land-surveying. In particular, the ancient Egyptian
Ancient Egypt () was a cradle of civilization concentrated along the lower reaches of the Nile River in Northeast Africa. It emerged from prehistoric Egypt around 3150BC (according to conventional Egyptian chronology), when Upper and Lower E ...
s paid attention to geometry and numbers, and the ancient Phoenicians performed practical arithmetic, book-keeping
Bookkeeping is the recording of financial transactions, and is part of the process of accounting in business and other organizations. It involves preparing source documents for all transactions, operations, and other events of a business. T ...
, navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
, and land-surveying. The results attained by these people seem to have been accessible (under certain conditions) to travelers, facilitating dispersal of the methods. It is probable that the knowledge of the Egyptians and Phoenicians was largely the result of observation
Observation in the natural sciences is an act or instance of noticing or perceiving and the acquisition of information from a primary source. In living beings, observation employs the senses. In science, observation can also involve the percep ...
and measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events.
In other words, measurement is a process of determining how large or small a physical quantity is as compared to ...
, and represented the accumulated experience of many ages. Subsequent studies of mathematics by the Greeks were largely indebted to these previous investigations.
Beginning of notation
 Written mathematics began with numbers expressed as
Written mathematics began with numbers expressed as tally marks
Tally marks, also called hash marks, are a form of numeral used for counting. They can be thought of as a unary numeral system.
They are most useful in counting or tallying ongoing results, such as the score in a game or sport, as no inter ...
, with each tally representing a single unit. Numerical symbols consisted probably of strokes or notches cut in wood or stone, which were intelligible across cultures. For example, one notch in a bone represented one animal, person, or object. Numerical notation's distinctive feature—symbols having both local and intrinsic values—implies a state of civilization
A civilization (also spelled civilisation in British English) is any complex society characterized by the development of state (polity), the state, social stratification, urban area, urbanization, and symbolic systems of communication beyon ...
at the period of its invention.
The earliest evidence of written mathematics dates back to the ancient Sumer
Sumer () is the earliest known civilization, located in the historical region of southern Mesopotamia (now south-central Iraq), emerging during the Chalcolithic and Early Bronze Age, early Bronze Ages between the sixth and fifth millennium BC. ...
ians and the system of metrology
Metrology is the scientific study of measurement. It establishes a common understanding of Unit of measurement, units, crucial in linking human activities. Modern metrology has its roots in the French Revolution's political motivation to stan ...
from 3000 BC. From around 2500 BC onwards, the Sumerians wrote multiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication binary operation, operation for an algebraic system.
The decimal multiplication table was traditionally tau ...
s on clay tablets and dealt with geometrical exercises and division problems. The earliest traces of Babylonian numerals also date back to this period. Babylonian mathematics has been reconstructed from more than 400 clay tablets unearthed since the 1850s. Written in cuneiform
Cuneiform is a Logogram, logo-Syllabary, syllabic writing system that was used to write several languages of the Ancient Near East. The script was in active use from the early Bronze Age until the beginning of the Common Era. Cuneiform script ...
, these tablets were inscribed whilst the clay was soft and then baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework.
The majority of Mesopotamian clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular numbers, reciprocals, and pairs. The tablets also include multiplication tables and methods for solving linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
and quadratic equation
In mathematics, a quadratic equation () is an equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where the variable (mathematics), variable represents an unknown number, and , , and represent known numbers, where . (If and ...
s. The Babylonian tablet YBC 7289
YBC 7289 is a Babylonian clay tablet notable for containing an accurate sexagesimal approximation to the square root of 2, the length of the diagonal of a unit square. This number is given to the equivalent of six decimal digits, "the greatest kn ...
gives an approximation of that is accurate to an equivalent of six decimal places.
Babylonian mathematics were written using a sexagesimal
Sexagesimal, also known as base 60, is a numeral system with 60 (number), sixty as its radix, base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified fo ...
(base-60) numeral system
A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symbols may represent differe ...
. From this derives the modern-day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 × 6) degrees in a circle, as well as the use of minutes and seconds of arc to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors: the reciprocal of any integer which is a multiple of divisors of 60 has a finite expansion in base 60. (In decimal arithmetic, only reciprocals of multiples of 2 and 5 have finite decimal expansions.) Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context.
Initially, the Mesopotamians
Mesopotamia is a historical region of West Asia situated within the Tigris–Euphrates river system, in the northern part of the Fertile Crescent. Today, Mesopotamia is known as present-day Iraq and forms the eastern geographic boundary of ...
had symbols for each power of ten. Later, they wrote numbers in almost exactly the same way as in modern times. Instead of using unique symbols for each power of ten, they wrote only the coefficient
In mathematics, a coefficient is a Factor (arithmetic), multiplicative factor involved in some Summand, term of a polynomial, a series (mathematics), series, or any other type of expression (mathematics), expression. It may be a Dimensionless qu ...
s of each power of ten, with each digit separated by only a space. By the time of Alexander the Great
Alexander III of Macedon (; 20/21 July 356 BC – 10/11 June 323 BC), most commonly known as Alexander the Great, was a king of the Ancient Greece, ancient Greek kingdom of Macedonia (ancient kingdom), Macedon. He succeeded his father Philip ...
, they had created a symbol that represented zero and was a placeholder.
Rhetorical algebra was first developed by the ancient Babylonians
Babylonia (; , ) was an ancient Akkadian-speaking state and cultural area based in the city of Babylon in central-southern Mesopotamia (present-day Iraq and parts of Kuwait, Syria and Iran). It emerged as an Akkadian-populated but Amorite-ru ...
and remained dominant up to the 16th century. In this system, equations are written in full sentences. For example, the rhetorical form of is "The thing plus one equals two" or possibly "The thing plus 1 equals 2".
The ancient Egyptians numerated by hieroglyphics. Egyptian mathematics had symbols for one, ten, one hundred, one thousand, ten thousand, one hundred thousand, and one million. Smaller digits were placed on the left of the number, as they are in Hindu–Arabic numerals. Later, the Egyptians used hieratic
Hieratic (; ) is the name given to a cursive writing system used for Ancient Egyptian and the principal script used to write that language from its development in the third millennium BCE until the rise of Demotic in the mid-first millennium BCE ...
instead of hieroglyphic
Ancient Egyptian hieroglyphs ( ) were the formal writing system used in Ancient Egypt for writing the Egyptian language. Hieroglyphs combined ideographic, logographic, syllabic and alphabetic elements, with more than 1,000 distinct characters. ...
script to show numbers. Hieratic was more like cursive and replaced several groups of symbols with individual ones. For example, the four vertical lines used to represent the number 'four' were replaced by a single horizontal line. This is found in the Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus (RMP; also designated as papyrus British Museum 10057, pBM 10058, and Brooklyn Museum 37.1784Ea-b) is one of the best known examples of ancient Egyptian mathematics.
It is one of two well-known mathematical papyri ...
(c. 2000–1800 BC) and the Moscow Mathematical Papyrus
The Moscow Mathematical Papyrus, also named the Golenishchev Mathematical Papyrus after its first non-Egyptian owner, Egyptologist Vladimir Golenishchev, is an ancient Egyptian mathematical papyrus containing several problems in arithmetic, ge ...
(c. 1890 BC). The system the Egyptians used was discovered and modified by many other civilizations in the Mediterranean. The Egyptians also had symbols for basic operations: legs going forward represented addition, and legs walking backward to represent subtraction.
The peoples with whom the Greeks of Asia Minor (amongst whom notation in western history begins) were likely to have come into frequent contact were those inhabiting the eastern littoral
The littoral zone, also called litoral or nearshore, is the part of a sea, lake, or river that is close to the shore. In coastal ecology, the littoral zone includes the intertidal zone extending from the high water mark (which is rarely i ...
of the Mediterranean; Greek tradition uniformly assigned the special development of geometry to the Egyptians, and the science of numbers to either the Egyptians or the Phoenicians.
Syncopated stage
The history of mathematics cannot with certainty be traced back to any school or period before that of the Ionian Greeks. Still, the subsequent history may be divided into periods, the distinctions between which are tolerably well-marked.Greek mathematics
Ancient Greek mathematics refers to the history of mathematical ideas and texts in Ancient Greece during Classical antiquity, classical and late antiquity, mostly from the 5th century BC to the 6th century AD. Greek mathematicians lived in cities ...
, which originated with the study of geometry, tended to be deductive and scientific from its commencement. Since the fourth century AD, Pythagoras
Pythagoras of Samos (; BC) was an ancient Ionian Greek philosopher, polymath, and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of P ...
has commonly been given credit for discovering the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, a theorem in geometry that states that in a right-angled triangle the area of the square on the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares of the other two sides.That is, . However, this geometric relationship appears in a few earlier ancient mathematical texts (albeit not as a formalized theorem), notably Plimpton 322
Plimpton 322 is a Babylonian clay tablet, believed to have been written around 1800 BC, that contains a mathematical table written in cuneiform script. Each row of the table relates to a Pythagorean triple, that is, a triple of integers (s ...
, a Babylonian tablet of mathematics from around 1900 BC. The study of mathematics as a subject in its own right began in the 6th century BC with the Pythagoreans
Pythagoreanism originated in the 6th century BC, based on and around the teachings and beliefs held by Pythagoras and his followers, the Pythagoreans. Pythagoras established the first Pythagorean community in the Ancient Greece, ancient Greek co ...
, who coined the term "mathematics" from the ancient Greek ''mathema'' (μάθημα), meaning "subject of instruction".
Plato
Plato ( ; Greek language, Greek: , ; born BC, died 348/347 BC) was an ancient Greek philosopher of the Classical Greece, Classical period who is considered a foundational thinker in Western philosophy and an innovator of the writte ...
's influence was especially strong in mathematics and the sciences. He helped to distinguish between pure and applied mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a ...
by widening the gap between "arithmetic" (now called number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
) and "logistic" (now called arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
). Greek mathematics greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor
Rigour (British English) or rigor (American English; see spelling differences) describes a condition of stiffness or strictness. These constraints may be environmentally imposed, such as "the rigours of famine"; logically imposed, such as mat ...
in proofs) and expanded the subject matter of mathematics. Aristotle
Aristotle (; 384–322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, a ...
is credited with what later would be called the law of excluded middle
In logic, the law of excluded middle or the principle of excluded middle states that for every proposition, either this proposition or its negation is true. It is one of the three laws of thought, along with the law of noncontradiction and t ...
.
Abstract or pure mathematics
Pure mathematics is the study of mathematical concepts independently of any application outside mathematics. These concepts may originate in real-world concerns, and the results obtained may later turn out to be useful for practical applications ...
deals with concepts like magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
and quantity
Quantity or amount is a property that can exist as a multitude or magnitude, which illustrate discontinuity and continuity. Quantities can be compared in terms of "more", "less", or "equal", or by assigning a numerical value multiple of a u ...
without regard to any practical application or situation, and includes arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
and geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
. In contrast, in mixed or applied mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a ...
, mathematical properties and relationships are applied to real-world objects to model laws of physics, for example in hydrostatics
Hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body". The word "hydrostatics" is sometimes used to refer specifically to water and ...
, optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
, and navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
.The new encyclopædia; or, Universal dictionary of arts and sciences. By Encyclopaedia Perthensi. Pg 49
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
is generally considered to be the greatest mathematician of antiquity and one of the greatest of all time. He used the method of exhaustion
The method of exhaustion () is a method of finding the area of a shape by inscribing inside it a sequence of polygons (one at a time) whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the differ ...
to calculate the area under the arc of a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
with the summation of an infinite series, and gave a remarkably accurate approximation of pi. He also defined the spiral
In mathematics, a spiral is a curve which emanates from a point, moving further away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.
Two-dimensional
A two-dimension ...
bearing his name, formulae for the volumes of surfaces of revolution, and an ingenious system for expressing very large numbers.
 The ancient Greeks made steps in the abstraction of geometry. Euclid's ''Elements'' (c. 300 BC) is the earliest extant documentation of the axioms of plane geometry—though Proclus tells of an earlier axiomatisation by
The ancient Greeks made steps in the abstraction of geometry. Euclid's ''Elements'' (c. 300 BC) is the earliest extant documentation of the axioms of plane geometry—though Proclus tells of an earlier axiomatisation by Hippocrates of Chios
Hippocrates of Chios (; c. 470 – c. 421 BC) was an ancient Greek mathematician, geometer, and astronomer.
He was born on the isle of Chios, where he was originally a merchant. After some misadventures (he was robbed by either pirates or ...
—and is one of the oldest extant Greek mathematical treatises. Consisting of thirteen books, it collects theorems proven by other mathematicians, supplemented by some original work. The document is a successful collection of definitions, postulates (axioms), propositions (theorems and constructions), and mathematical proofs of the propositions, and covers topics such as Euclidean geometry, geometric algebra, elementary number theory, and the ancient Greek version of algebraic systems. The first theorem given in the text, Euclid's lemma
In algebra and number theory, Euclid's lemma is a lemma that captures a fundamental property of prime numbers:
For example, if , , , then , and since this is divisible by 19, the lemma implies that one or both of 133 or 143 must be as well. In ...
, captures a fundamental property of prime number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime ...
s. The text was ubiquitous in the ''quadrivium
From the time of Plato through the Middle Ages, the ''quadrivium'' (plural: quadrivia) was a grouping of four subjects or arts—arithmetic, geometry, music, and astronomy—that formed a second curricular stage following preparatory work in th ...
'' and was instrumental in the development of logic, mathematics, and science. Autolycus
In Greek mythology, Autolycus (; ) was a robber who had the power to metamorphose or make invisible the things he stole. He had his residence on Mount Parnassus and was renowned among men for his cunning and oaths.
Family
There are a number of d ...
' '' On the Moving Sphere'' is another ancient mathematical manuscript of the time.
The next phase of notation for algebra was syncopated algebra, in which some symbolism is used, but which does not contain all of the characteristics of symbolic algebra. For instance, there may be a restriction that subtraction may be used only once within one side of an equation, which is not the case with symbolic algebra. Syncopated algebraic expression first appeared
In comic books and other stories with a long history, first appearance refers to the first issue to feature a fictional character. These issues are often highly valued by collectors due to their rarity and iconic status.
Reader interest in fir ...
in a serious of books called ''Arithmetica
Diophantus of Alexandria () (; ) was a Greek mathematics, Greek mathematician who was the author of the ''Arithmetica'' in thirteen books, ten of which are still extant, made up of arithmetical problems that are solved through algebraic equations ...
'', by Diophantus of Alexandria (3rd century AD; many lost), followed by Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
's '' Brahma Sphuta Siddhanta'' (7th century).
Acrophonic and Milesian numeration
The ancient Greeks employed Attic numeration,Mathematics and Measurement By Oswald Ashton Wentworth Dilk. P14
/ref> which was based on the system of the Egyptians and was later adapted and used by the Romans. Greek numerals one through four were written as vertical lines, as in the hieroglyphics. The symbol for five was the Greek letter Π (pi), representing the Greek word for 'five' (''pente''). Numbers six through nine were written as a Π with vertical lines beside it. Ten was represented by the letter Δ (delta), from word for 'ten' (''deka''), one hundred by the letter from the word for hundred, and so on. This system was 'acrophonic' since it was based on the first sound of the numeral. Milesian (Ionian) numeration was another Greek numeral system. It was constructed by partitioning the twenty-four letters of the Greek alphabet, plus three archaic letters, into three classes of nine letters each, and using them to represent the units, tens, and hundreds. (
Jean Baptiste Joseph Delambre
Jean Baptiste Joseph, chevalier Delambre (19 September 1749 – 19 August 1822) was a French mathematician, astronomer, historian of astronomy, and geodesist. He was also director of the Paris Observatory, and author of well-known books on the ...
's Astronomie Ancienne, t. ii.)
This system appeared in the third century BC, before the letters digamma (Ϝ), koppa (Ϟ), and sampi (Ϡ) became obsolete. When lowercase letters became differentiated from uppercase letters, the lowercase letters were used as the symbols for notation. Multiples of one thousand were written as the nine numbers with a stroke in front of them: thus, one thousand was ",α", two thousand was ",β", etc. The letter M (for ''μύριοι'', as in "myriad") was used to multiply numbers by ten thousand. For example, the number 88,888,888 would be written as M,ηωπη*ηωπη.Boyer, Carl B. ''A History of Mathematics'', 2nd edition, John Wiley & Sons, Inc., 1991.
Milesian numeration, though far less convenient than modern numerals, was formed on a perfectly regular and scientific plan,A dictionary of science, literature and art, ed. by W.T. Brande. P683
/ref> and could be used with tolerable effect as an instrument of calculation, to which purpose the Roman system was totally inapplicable. Greek mathematical reasoning was almost entirely geometric (albeit often used to reason about non-geometric subjects such as
number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
), and hence the Greeks had no interest in algebraic symbols. An exception was the great algebraist Diophantus
Diophantus of Alexandria () (; ) was a Greek mathematician who was the author of the '' Arithmetica'' in thirteen books, ten of which are still extant, made up of arithmetical problems that are solved through algebraic equations.
Although Jose ...
of Alexandria
Alexandria ( ; ) is the List of cities and towns in Egypt#Largest cities, second largest city in Egypt and the List of coastal settlements of the Mediterranean Sea, largest city on the Mediterranean coast. It lies at the western edge of the Nile ...
. His ''Arithmetica
Diophantus of Alexandria () (; ) was a Greek mathematics, Greek mathematician who was the author of the ''Arithmetica'' in thirteen books, ten of which are still extant, made up of arithmetical problems that are solved through algebraic equations ...
'' was one of the texts to use symbols in equations. It was not completely symbolic, but was much more so than previous books. In it, an unknown number was called ''s''; the square of ''s'' was ; the cube was ; the fourth power was ; and the fifth power was . So for example, the expression:
:
would be written as:
:
Chinese mathematical notation
Roman numeral
Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written with combinations of letters from the Latin alphabet, ea ...
for ten. Nowadays, this ''huama'' numeral system is only used for displaying prices in Chinese markets or on traditional handwritten invoices.
Mathematics in China emerged independently by the 11th century BC, but has much older roots. The ancient Chinese were acquainted with astronomical cycles, geometrical implements like the rule, compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with No ...
, and plumb-bob
A plumb bob, plumb bob level, or plummet, is a weight, usually with a pointed tip on the bottom, suspended from a string and used as a vertical direction as a reference line, or plumb-line. It is a precursor to the spirit level and used to esta ...
, and machines like the wheel
A wheel is a rotating component (typically circular in shape) that is intended to turn on an axle Bearing (mechanical), bearing. The wheel is one of the key components of the wheel and axle which is one of the Simple machine, six simple machin ...
and axle
An axle or axletree is a central shaft for a rotation, rotating wheel and axle, wheel or gear. On wheeled vehicles, the axle may be fixed to the wheels, rotating with them, or fixed to the vehicle, with the wheels rotating around the axle. In ...
. The Chinese independently developed very large and negative number
In mathematics, a negative number is the opposite (mathematics), opposite of a positive real number. Equivalently, a negative number is a real number that is inequality (mathematics), less than 0, zero. Negative numbers are often used to represe ...
s, decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
s, a place value decimal system, a binary system, algebra, geometry, and trigonometry. As in other early societies, the purpose of astronomy was to perfect the agricultural calendar and other practical tasks, not to establish a formal system
A formal system is an abstract structure and formalization of an axiomatic system used for deducing, using rules of inference, theorems from axioms.
In 1921, David Hilbert proposed to use formal systems as the foundation of knowledge in ma ...
; thus, the duties of the Chinese Board of Mathematics were confined to the annual preparation of the dates and predictions of the almanac.
counting rods
Counting rods (筭) are small bars, typically 3–14 cm (1" to 6") long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number.
...
(which emerged during the Warring States period
The Warring States period in history of China, Chinese history (221 BC) comprises the final two and a half centuries of the Zhou dynasty (256 BC), which were characterized by frequent warfare, bureaucratic and military reforms, and ...
), certain geometrical theorems (such as the ratio of sides), and the '' suanpan'' (abacus) for performing arithmetic calculations. Mathematical results were expressed in writing. Ancient Chinese mathematicians did not develop an axiomatic approach, but made advances in algorithm development and algebra. Chinese algebra reached its zenith in the 13th century, when Zhu Shijie invented the method of four unknowns. Early China exemplifies how a civilization may possess considerable skill in the applied arts with only scarce understanding of the formal mathematics on which those arts are founded.
Due to linguistic and geographic barriers, as well as content, the mathematics of ancient China and the mathematics of the ancient Mediterranean world are presumed to have developed more or less independently. The final form of ''The Nine Chapters on the Mathematical Art
''The Nine Chapters on the Mathematical Art'' is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE. This book is one of the earliest surviving ...
'' and the '' Book on Numbers and Computation'' and ''Huainanzi
The ''Huainanzi'' is an ancient Chinese text made up of essays from scholarly debates held at the court of Liu An, Prince of Huainan, before 139 BCE. Compiled as a handbook for an enlightened sovereign and his court, the work attempts to defi ...
'' are roughly contemporary with classical Greek mathematics. Some exchange of ideas across Asia through known cultural exchanges from at least Roman times is likely. Frequently, elements of the mathematics of early societies correspond to rudimentary results found later in branches of modern mathematics such as geometry or number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
. For example, the Pythagorean theorem was attested in the ''Zhoubi Suanjing
The ''Zhoubi Suanjing'', also known by many other names, is an ancient Chinese astronomical and mathematical work. The ''Zhoubi'' is most famous for its presentation of Chinese cosmology and a form of the Pythagorean theorem. It claims to pr ...
'', and knowledge of Pascal's triangle
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Bla ...
has also been shown to have existed in China centuries before Blaise Pascal
Blaise Pascal (19June 162319August 1662) was a French mathematician, physicist, inventor, philosopher, and Catholic Church, Catholic writer.
Pascal was a child prodigy who was educated by his father, a tax collector in Rouen. His earliest ...
, articulated by mathematicians like the polymath Shen Kuo
Shen Kuo (; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and Art name#China, pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁),Yao (2003), 544. was a Chinese polymath, scientist, and statesman of the Song dynasty (960� ...
.
The state of trigonometry advanced during the Song dynasty (960–1279), when Chinese mathematicians had greater need of spherical trigonometry in calendrical science and astronomical calculations. Shen Kuo
Shen Kuo (; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and Art name#China, pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁),Yao (2003), 544. was a Chinese polymath, scientist, and statesman of the Song dynasty (960� ...
used trigonometric functions to solve mathematical problems of chords and arcs.Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd. Shen's work on arc lengths provided the basis for spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, ge ...
developed in the 13th century by the mathematician and astronomer Guo Shoujing
Guo Shoujing (, 1231–1316), courtesy name Ruosi (), was a Chinese astronomer, hydraulic engineer, mathematician, and politician of the Yuan dynasty. The later Johann Adam Schall von Bell (1591–1666) was so impressed with the preserved astro ...
. Sal Restivo As the historians L. Gauchet and Joseph Needham state, Guo Shoujing used spherical trigonometry in his calculations to improve the calendar system and Chinese astronomy
Astronomy in China has a long history stretching from the Shang dynasty, being refined over a period of more than 3,000 years. The Ancient China, ancient Chinese people have identified stars from 1300 BCE, as Chinese star names later categori ...
. Marcel Gauchet, 151. Chinese mathematics later incorporated the work and teaching of Arab missionaries with knowledge of spherical trigonometry who had come to China during the 13th century.
Indian and Arabic numerals and notation
TheHindu–Arabic numeral system
The Hindu–Arabic numeral system (also known as the Indo-Arabic numeral system, Hindu numeral system, and Arabic numeral system) is a positional notation, positional Decimal, base-ten numeral system for representing integers; its extension t ...
and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India
India, officially the Republic of India, is a country in South Asia. It is the List of countries and dependencies by area, seventh-largest country by area; the List of countries by population (United Nations), most populous country since ...
and was transmitted to the west via Islamic mathematics. Islamic mathematics developed and expanded the mathematics known to Central Asia
Central Asia is a region of Asia consisting of Kazakhstan, Kyrgyzstan, Tajikistan, Turkmenistan, and Uzbekistan. The countries as a group are also colloquially referred to as the "-stans" as all have names ending with the Persian language, Pers ...
n civilizations, including the addition of the decimal point
FIle:Decimal separators.svg, alt=Four types of separating decimals: a) 1,234.56. b) 1.234,56. c) 1'234,56. d) ١٬٢٣٤٫٥٦., Both a comma and a full stop (or period) are generally accepted decimal separators for international use. The apost ...
notation to the Arabic numerals
The ten Arabic numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) are the most commonly used symbols for writing numbers. The term often also implies a positional notation number with a decimal base, in particular when contrasted with Roman numera ...
.
The algebraic notation of the Indian mathematician Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
was syncopated
In music, syncopation is a variety of rhythms played together to make a piece of music, making part or all of a tune or piece of music off-beat (music), off-beat. More simply, syncopation is "a disturbance or interruption of the regular flow of ...
(that is, some operations and quantities had symbolic representations). Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend (the number to be subtracted), and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms.
Despite their name, Arabic numerals
The ten Arabic numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) are the most commonly used symbols for writing numbers. The term often also implies a positional notation number with a decimal base, in particular when contrasted with Roman numera ...
have roots in India. The reason for this misnomer
A misnomer is a name that is incorrectly or unsuitably applied. Misnomers often arise because something was named long before its correct nature was known, or because an earlier form of something has been replaced by a later form to which the nam ...
is Europeans saw the numerals used in an Arabic book, ''Concerning the Hindu Art of Reckoning'', by Muhammed ibn-Musa al-Khwarizmi. Al-Khwārizmī wrote several important books on the Hindu–Arabic numerals and on methods for solving equations. His book ''On the Calculation with Hindu Numerals'' (c. 825), along with the work of Al-Kindi
Abū Yūsuf Yaʻqūb ibn ʼIsḥāq aṣ-Ṣabbāḥ al-Kindī (; ; ; ) was an Arab Muslim polymath active as a philosopher, mathematician, physician, and music theorist
Music theory is the study of theoretical frameworks for understandin ...
, were instrumental in spreading Indian mathematics and numerals to the West. Al-Khwarizmi did not claim the numerals as Arabic, but over several Latin translations, the fact that the numerals were Indian in origin was lost. The word ''algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
'' is derived from the Latinization of Al-Khwārizmī's name, Algoritmi, and the word ''algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...
'' from the title of one of his works, '' Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa'l-muqābala'' (''The Compendious Book on Calculation by Completion and Balancing'').
The modern Arabic numeral
The ten Arabic numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) are the most commonly used symbols for writing numbers. The term often also implies a positional notation number with a decimal base, in particular when contrasted with Roman numerals. ...
symbols used around the world first appeared in Islamic North Africa
North Africa (sometimes Northern Africa) is a region encompassing the northern portion of the African continent. There is no singularly accepted scope for the region. However, it is sometimes defined as stretching from the Atlantic shores of t ...
in the 10th century. A distinctive Western Arabic variant of the Eastern Arabic numerals
The Eastern Arabic numerals, also called Indo-Arabic numerals or Arabic-Indic numerals as known by Unicode, are the symbols used to represent numerical digits in conjunction with the Arabic alphabet in the countries of the Mashriq (the east o ...
began to emerge around the 10th century in the Maghreb
The Maghreb (; ), also known as the Arab Maghreb () and Northwest Africa, is the western part of the Arab world. The region comprises western and central North Africa, including Algeria, Libya, Mauritania, Morocco, and Tunisia. The Maghreb al ...
and Al-Andalus
Al-Andalus () was the Muslim-ruled area of the Iberian Peninsula. The name refers to the different Muslim states that controlled these territories at various times between 711 and 1492. At its greatest geographical extent, it occupied most o ...
(sometimes called ''ghubar'' numerals, though the term is not always accepted), which are the direct ancestor of the modern Arabic numerals used throughout the world.
Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe. In the 12th century, scholars traveled to Spain and Sicily seeking scientific Arabic texts, including al-Khwārizmī's (translated into Latin by Robert of Chester) and the complete text of Euclid's ''Elements'' (translated in various versions by Adelard of Bath
Adelard of Bath (; 1080? 1142–1152?) was a 12th-century English natural philosopher. He is known both for his original works and for translating many important Greek scientific works of astrology, astronomy, philosophy, alchemy and mathemat ...
, Herman of Carinthia
Herman of Carinthia (1105/1110 – after 1154), also called Hermanus Dalmata or Sclavus Dalmata, Secundus, by his own words born in the "heart of Istria", was a philosopher, astronomer, astrologer, mathematician and translator of Arabic works int ...
, and Gerard of Cremona
Gerard of Cremona (Latin: ''Gerardus Cremonensis''; c. 1114 – 1187) was an Italians, Italian translator of scientific books from Arabic into Latin. He worked in Toledo, Spain, Toledo, Kingdom of Castile and obtained the Arabic books in the libr ...
). One of the European books that advocated using the numerals was ''Liber Abaci
The or (Latin for "The Book of Calculation") was a 1202 Latin work on arithmetic by Leonardo of Pisa, posthumously known as Fibonacci. It is primarily famous for introducing both base-10 positional notation and the symbols known as Arabic n ...
'', by Leonardo of Pisa, better known as Fibonacci
Leonardo Bonacci ( – ), commonly known as Fibonacci, was an Italians, Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages".
The name he is commonly called, ''Fibonacci ...
. ''Liber Abaci'' is better known for containing a mathematical problem in which the growth of a rabbit population ends up being the Fibonacci sequence
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many w ...
.
Symbolic stage
;Symbols by popular introduction dateminus
The plus sign () and the minus sign () are mathematical symbols used to denote positive and negative functions, respectively. In addition, the symbol represents the operation of addition, which results in a sum, while the symbol represent ...
"
at:1525 shift:(0,17) text:" radical"
at:1544 shift:(0,28) text:" parenth."
at:1557 shift:(0,39) text:" equals"
at:1618 shift:(0,3) text:" multiply"
at:1628 shift:(0,14) text:" plus-minus"
at:1628 shift:(0,25) text:" proportion"
at:1629 shift:(0,36) text:" radical"
at:1631 shift:(0,47) text:" inequality"
at:1636 shift:(0,58) text:"superscript
A subscript or superscript is a character (such as a number or letter) that is set slightly below or above the normal line of type, respectively. It is usually smaller than the rest of the text. Subscripts appear at or below the baseline, wh ...
"
at:1637 shift:(0,69) text:" radical"
at:1650 shift:(0,80) text:"percent
In mathematics, a percentage () is a number or ratio expressed as a fraction of 100. It is often denoted using the ''percent sign'' (%), although the abbreviations ''pct.'', ''pct'', and sometimes ''pc'' are also used. A percentage is a dime ...
"
at:1655 shift:(0,91) text:"infinity
Infinity is something which is boundless, endless, or larger than any natural number. It is denoted by \infty, called the infinity symbol.
From the time of the Ancient Greek mathematics, ancient Greeks, the Infinity (philosophy), philosophic ...
"
at:1659 shift:(0,102) text:" division"
at:1670 shift:(0,113) text: Inequality"
at:1675 shift:(0,124) text: differential"
at:1675 shift:(0,135) text:integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
"
at:1684 shift:(0,146) text: colon"
at:1698 shift:(0,157) text: dot"
at:1718 shift:(0,5) text:slash
Slash may refer to:
* Slash (punctuation), the "/" character
Arts and entertainment Fictional characters
* Slash (Marvel Comics)
* Slash (''Teenage Mutant Ninja Turtles'')
Music
* Harry Slash & The Slashtones, an American rock band
* Nash th ...
"
at:1734 shift:(0,15) text: inequality"
at:1755 shift:(0,25) text:summation
In mathematics, summation is the addition of a sequence of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, pol ...
"
at:1768 shift:(0,35) text: proportionality"
at:1770 shift:(0,45) text: differential"
at:1770 shift:(0,55) text:prime
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
"
at:1801 shift:(0,65) text: identity"
at:1808 shift:(0,75) text:integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
"
at:1808 shift:(0,85) text:factorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times ...
"
at:1812 shift:(0,95) text: product"
at:1817 shift:(0,105) text:inclusion
Inclusion or Include may refer to:
Sociology
* Social inclusion, action taken to support people of different backgrounds sharing life together.
** Inclusion (disability rights), promotion of people with disabilities sharing various aspects of lif ...
"
at:1841 shift:(0,115) text: abs."
at:1841 shift:(0,125) text: determ."
at:1843 shift:(0,135) text: line matrix"
at:1846 shift:(0,145) text:" nabla"
at:1888 shift:(0,17) text:" union~Intersection
In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their ...
"
at:1890 shift:(0,28) text:"inclusion
Inclusion or Include may refer to:
Sociology
* Social inclusion, action taken to support people of different backgrounds sharing life together.
** Inclusion (disability rights), promotion of people with disabilities sharing various aspects of lif ...
"
at:1893 shift:(0,39) text:"aleph
Aleph (or alef or alif, transliterated ʾ) is the first Letter (alphabet), letter of the Semitic abjads, including Phoenician alphabet, Phoenician ''ʾālep'' 𐤀, Hebrew alphabet, Hebrew ''ʾālef'' , Aramaic alphabet, Aramaic ''ʾālap'' � ...
"
at:1894 shift:(0,50) text:"membership
Member may refer to:
* Military jury, referred to as "Members" in military jargon
* Element (mathematics), an object that belongs to a mathematical set
* In object-oriented programming, a member of a class
** Field (computer science), entries in ...
"
at:1895 shift:(0,61) text:" braces"
at:1895 shift:(0,72) text:" N"
at:1897 shift:(0,83) text:" existential"
at:1902 shift:(0,94) text:"cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
"
at:1902 shift:(0,105) text:"dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
"
at:1906 shift:(0,116) text:"disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is ...
"
at:1909 shift:(0,127) text:" parenth. matrix"
at:1913 shift:(0,138) text:" box matrix"
at:1917 shift:(0,149) text:" contour"
at:1930 shift:(0,160) text:" Z, "
at:1930 shift:(12,160) text:" Q"
at:1935 shift:(0,171) text:" universals"
at:1936 shift:(0,182) text:"arrow
An arrow is a fin-stabilized projectile launched by a bow. A typical arrow usually consists of a long, stiff, straight shaft with a weighty (and usually sharp and pointed) arrowhead attached to the front end, multiple fin-like stabilizers c ...
"
at:1939 shift:(0,193) text:" empty"
at:1939 shift:(0,204) text:" C"
at:1940 shift:(0,215) text:"arrow
An arrow is a fin-stabilized projectile launched by a bow. A typical arrow usually consists of a long, stiff, straight shaft with a weighty (and usually sharp and pointed) arrowhead attached to the front end, multiple fin-like stabilizers c ...
"
at:1960 shift:(0,17) text:" EoP"
at:1960 shift:(3,5) text:" ∎"
at:1962 shift:(0,28) text:"integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
"
Early arithmetic and multiplication
The transition to symbolic algebra, where only symbols are used, can first be seen in the work ofIbn al-Banna' al-Marrakushi
Ibn al‐Bannāʾ al‐Marrākushī (), full name: Abu'l-Abbas Ahmad ibn Muhammad ibn Uthman al-Azdi al-Marrakushi () (29 December 1256 – 31 July 1321), was an Arab Muslim polymath who was active as a mathematician, astronomer, Islamic schol ...
(1256–1321) and Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī (1412–1482). Al-Qalasādī was the last major medieval Arab algebraist, who improved on the algebraic notation earlier used in the Maghreb
The Maghreb (; ), also known as the Arab Maghreb () and Northwest Africa, is the western part of the Arab world. The region comprises western and central North Africa, including Algeria, Libya, Mauritania, Morocco, and Tunisia. The Maghreb al ...
by Ibn al-Banna. In contrast to the syncopated notations of their predecessors, Diophantus
Diophantus of Alexandria () (; ) was a Greek mathematician who was the author of the '' Arithmetica'' in thirteen books, ten of which are still extant, made up of arithmetical problems that are solved through algebraic equations.
Although Jose ...
and Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
, which lacked symbols for mathematical operations, al-Qalasadi's algebraic notation was the first to have symbols for these functions and was thus "the first steps toward the introduction of algebraic symbolism". He represented mathematical symbols using characters from the Arabic alphabet
The Arabic alphabet, or the Arabic abjad, is the Arabic script as specifically codified for writing the Arabic language. It is a unicase, unicameral script written from right-to-left in a cursive style, and includes 28 letters, of which most ...
.
 The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. The two most widely used arithmetic symbols are addition and subtraction, + and −. The
The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. The two most widely used arithmetic symbols are addition and subtraction, + and −. The plus sign
The plus sign () and the minus sign () are mathematical symbols used to denote positive and negative functions, respectively. In addition, the symbol represents the operation of addition, which results in a sum, while the symbol represents ...
was used starting around 1351 by Nicole Oresme
Nicole Oresme (; ; 1 January 1325 – 11 July 1382), also known as Nicolas Oresme, Nicholas Oresme, or Nicolas d'Oresme, was a French philosopher of the later Middle Ages. He wrote influential works on economics, mathematics, physics, astrology, ...
and publicized in his work ''Algorismus proportionum'' (1360). It is thought to be an abbreviation for "et", meaning "and" in Latin, in much the same way the ampersand
The ampersand, also known as the and sign, is the logogram , representing the grammatical conjunction, conjunction "and". It originated as a typographic ligature, ligature of the letters of the word (Latin for "and").
Etymology
Tradi ...
sign also began as "et". Oresme at the University of Paris
The University of Paris (), known Metonymy, metonymically as the Sorbonne (), was the leading university in Paris, France, from 1150 to 1970, except for 1793–1806 during the French Revolution. Emerging around 1150 as a corporation associated wit ...
and the Italian Giovanni di Casali independently provided graphical demonstrations of the distance covered by a body undergoing uniformly accelerated motion, asserting that the area under the line depicting the constant acceleration and represented the total distance traveled. The minus sign
The plus sign () and the minus sign () are mathematical symbols used to denote positive and negative functions, respectively. In addition, the symbol represents the operation of addition, which results in a sum, while the symbol represent ...
was used in 1489 by Johannes Widmann
Johannes Widmann (c. 1460 – after 1498) was a German mathematician. The + and - symbols first appeared in print in his book ''Mercantile Arithmetic'' or ''Behende und hüpsche Rechenung auff allen Kauffmanschafft'' published in Leipzig in 1489 ...
in ''Mercantile Arithmetic'' or ''Behende und hüpsche Rechenung auff allen Kauffmanschafft''. Widmann used the minus symbol with the plus symbol to indicate deficit and surplus, respectively. In '' Summa de arithmetica, geometria, proportioni e proportionalità'', Luca Pacioli
Luca Bartolomeo de Pacioli, O.F.M. (sometimes ''Paccioli'' or ''Paciolo''; 1447 – 19 June 1517) was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and an early contributor to the field now known as account ...
used plus and minus symbols and algebra, though much of the work originated from Piero della Francesca
Piero della Francesca ( , ; ; ; – 12 October 1492) was an Italian Renaissance painter, Italian painter, mathematician and List of geometers, geometer of the Early Renaissance, nowadays chiefly appreciated for his art. His painting is charact ...
whom he appropriated and purloined.
The radical symbol (√), for square root, was introduced by Christoph Rudolff in the early 1500s. Michael Stifel
Michael Stifel or Styfel (1487 – April 19, 1567) was a German monk, Protestant reformer and mathematician. He was an Augustinians, Augustinian who became an early supporter of Martin Luther. He was later appointed professor of mathematics at Je ...
's important work ''Arithmetica integra'' contained important innovations in mathematical notation. In 1556 Niccolò Tartaglia
Nicolo, known as Tartaglia (; 1499/1500 – 13 December 1557), was an Italian mathematician, engineer (designing fortifications), a surveyor (of topography, seeking the best means of defense or offense) and a bookkeeper from the then Republi ...
used parentheses for precedence grouping. In 1557 Robert Recorde
Robert Recorde () was a Welsh physician and mathematician. He invented the equals sign (=) and also introduced the pre-existing plus (+) and minus (−) signs to English speakers in 1557.
Biography
Born around 1510, Robert Recorde was the sec ...
published ''The Whetstone of Witte
''The Whetstone of Witte'' is the shortened title of Robert Recorde's mathematics book published in 1557, the full title being ''The whetstone of , is the : The ''Coßike'' practise, with the rule of ''Equation'': and the of ''Surde Nombers. ...
'', which introduced the equal sign (=), as well as plus and minus signs, to the English reader. In 1564 Gerolamo Cardano
Gerolamo Cardano (; also Girolamo or Geronimo; ; ; 24 September 1501– 21 September 1576) was an Italian polymath whose interests and proficiencies ranged through those of mathematician, physician, biologist, physicist, chemist, astrologer, as ...
analyzed games of chance
A game of chance is in contrast with a game of skill. It is a game whose outcome is strongly influenced by some randomizing device. Common devices used include dice, spinning tops, playing cards, roulette wheels, numbered balls, or in the case ...
beginning the early stages of probability theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expre ...
. Rafael Bombelli
Rafael Bombelli (baptised on 20 January 1526; died 1572) was an Italian mathematician. Born in Bologna, he is the author of a treatise on algebra and is a central figure in the understanding of imaginary numbers.
He was the one who finally manag ...
published his ''L'Algebra'' (1572) in which he showed how to deal with the imaginary quantities that could appear in Cardano's formula for solving cubic equations. Simon Stevin
Simon Stevin (; 1548–1620), sometimes called Stevinus, was a County_of_Flanders, Flemish mathematician, scientist and music theorist. He made various contributions in many areas of science and engineering, both theoretical and practical. He a ...
's book ''De Thiende'' ("The Art of Tenths"), published in Dutch in 1585, contained a systematic treatment of decimal notation
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of the ...
, which influenced all later work on the real number system
In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real ...
. The new algebra
New or NEW may refer to:
Music
* New, singer of K-pop group The Boyz
* ''New'' (album), by Paul McCartney, 2013
** "New" (Paul McCartney song), 2013
* ''New'' (EP), by Regurgitator, 1995
* "New" (Daya song), 2017
* "New" (No Doubt song), 1 ...
(1591) of François Viète
François Viète (; 1540 – 23 February 1603), known in Latin as Franciscus Vieta, was a French people, French mathematician whose work on new algebra was an important step towards modern algebra, due to his innovative use of letters as par ...
introduced the modern notational manipulation of algebraic expressions.
John Napier
John Napier of Merchiston ( ; Latinisation of names, Latinized as Ioannes Neper; 1 February 1550 – 4 April 1617), nicknamed Marvellous Merchiston, was a Scottish landowner known as a mathematician, physicist, and astronomer. He was the 8 ...
is best known as the inventor of logarithms
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
(published in '' Description of the Marvelous Canon of Logarithms'') and made common the use of the decimal point
FIle:Decimal separators.svg, alt=Four types of separating decimals: a) 1,234.56. b) 1.234,56. c) 1'234,56. d) ١٬٢٣٤٫٥٦., Both a comma and a full stop (or period) are generally accepted decimal separators for international use. The apost ...
in arithmetic and mathematics. After Napier, Edmund Gunter
Edmund Gunter (158110 December 1626), was an English clergyman, mathematician, geometer and astronomer of Welsh descent. He is best remembered for his mathematical contributions, which include the invention of the Gunter's chain, the #Gunter's q ...
created the logarithmic scale
A logarithmic scale (or log scale) is a method used to display numerical data that spans a broad range of values, especially when there are significant differences among the magnitudes of the numbers involved.
Unlike a linear Scale (measurement) ...
s (lines, or rules); William Oughtred
William Oughtred (5 March 1574 – 30 June 1660), also Owtred, Uhtred, etc., was an English mathematician and Anglican clergyman.'Oughtred (William)', in P. Bayle, translated and revised by J.P. Bernard, T. Birch and J. Lockman, ''A General ...
used two such scales sliding by one another to perform direct multiplication and division and is credited as the inventor of the slide rule
A slide rule is a hand-operated mechanical calculator consisting of slidable rulers for conducting mathematical operations such as multiplication, division, exponents, roots, logarithms, and trigonometry. It is one of the simplest analog ...
in 1622. In 1631 Oughtred introduced the multiplication sign (×), his proportionality sign (∷), and abbreviations 'sin' and 'cos' for the sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite th ...
and cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that ...
functions. Albert Girard also used the abbreviations 'sin', 'cos', and 'tan' for the trigonometric functions in his treatise.
René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
is credited as the father of analytical geometry, the bridge between algebra and geometry, crucial to the discovery of infinitesimal calculus
Calculus is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the calculus of ...
and analysis
Analysis (: analyses) is the process of breaking a complex topic or substance into smaller parts in order to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle (38 ...
. In the 17th century, Descartes introduced Cartesian co-ordinates which allowed the development of analytic geometry, bringing the notation of equations to geometry. Blaise Pascal
Blaise Pascal (19June 162319August 1662) was a French mathematician, physicist, inventor, philosopher, and Catholic Church, Catholic writer.
Pascal was a child prodigy who was educated by his father, a tax collector in Rouen. His earliest ...
influenced mathematics throughout his life; for instance, his ''Traité du triangle arithmétique'' ("Treatise on the Arithmetical Triangle") (1653) described a convenient tabular presentation for binomial coefficient
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers and is written \tbinom. It is the coefficient of the t ...
s, now called Pascal's triangle
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Bla ...
. John Wallis
John Wallis (; ; ) was an English clergyman and mathematician, who is given partial credit for the development of infinitesimal calculus.
Between 1643 and 1689 Wallis served as chief cryptographer for Parliament and, later, the royal court. ...
introduced the infinity symbol
The infinity symbol () is a mathematical symbol representing the concept of infinity. This symbol is also called a ''lemniscate'', after the lemniscate curves of a similar shape studied in algebraic geometry, or "lazy eight", in the terminolo ...
(∞) and also used this notation for infinitesimals
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the " ...
, for example, .
Johann Rahn
Johann Rahn (Latinised form Rhonius) (10 March 1622 – 25 May 1676) was a Swiss mathematician who is credited with the first use of the division sign, ÷ (a repurposed obelus
An obelus (plural: obeluses or obeli) is a term in codicology ...
introduced the division sign
The division sign () is a mathematical symbol consisting of a short horizontal line with a dot above and another dot below, used in Anglophone countries to indicate the operation of division. This usage is not universal and the symbol has d ...
(÷, an obelus
An obelus (plural: obeluses or obeli) is a term in codicology and latterly in typography that refers to a historical annotation mark which has resolved to three modern meanings:
* Division sign
* Dagger
* Commercial minus sign (limited g ...
variant repurposed) and the therefore sign (∴) in 1659. William Jones used π in ''Synopsis palmariorum mathesios'' in 1706 because it is the initial letter of the Greek word ''perimetron'' (περιμετρον), which means perimeter
A perimeter is the length of a closed boundary that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional line. The perimeter of a circle or an ellipse is called its circumference.
Calculating the perimet ...
in Greek. This usage was popularized in 1737 by Euler. In 1734, Pierre Bouguer
Pierre Bouguer () (16 February 1698, Le Croisic – 15 August 1758, Paris) was a French mathematician, geophysicist, geodesist, and astronomer. He is also known as "the father of naval architecture".
Career
Bouguer's father, Jean Bouguer, ...
used double horizontal bar below the inequality sign.
Derivatives notation: Leibniz and Newton
The study oflinear algebra
Linear algebra is the branch of mathematics concerning linear equations such as
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrix (mathemat ...
emerged from the study of determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...
s, which were used to solve systems of linear equation
In mathematics, a linear equation is an equation that may be put in the form
a_1x_1+\ldots+a_nx_n+b=0, where x_1,\ldots,x_n are the variables (or unknowns), and b,a_1,\ldots,a_n are the coefficients, which are often real numbers. The coeffici ...
s. Calculus had two main systems of notation, each created by one of its creators: that developed by Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
and that developed by Gottfried Leibniz
Gottfried Wilhelm Leibniz (or Leibnitz; – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Isaac Newton, Sir Isaac Newton, with the creation of calculus in ad ...
. Leibniz's notation is used most often today.
Newton's notation was simply a dot or dash placed above the function. For example, the derivative of the function ' would be written as . The second derivative of would be written as . In modern usage, this notation generally denotes derivatives of physical quantities with respect to time, and is used frequently in the science of mechanics
Mechanics () is the area of physics concerned with the relationships between force, matter, and motion among Physical object, physical objects. Forces applied to objects may result in Displacement (vector), displacements, which are changes of ...
. Leibniz, on the other hand, used the letter as a prefix to indicate differentiation, and introduced the notation representing derivatives as if they were a special type of fraction. For example, the derivative of the function with respect to the variable in Leibniz's notation would be written as . This notation makes explicit the variable with respect to which the derivative of the function is taken. Leibniz also created the integral symbol (). For example: . When finding areas under curves, integration is often illustrated by dividing the area into infinitely many tall, thin rectangles, whose areas are added. Thus, the integral symbol is an elongated S, representing the Latin
Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area aroun ...
word ''summa'', meaning "sum".
High division operators and functions
At this time, letters of the alphabet were to be used as symbols ofquantity
Quantity or amount is a property that can exist as a multitude or magnitude, which illustrate discontinuity and continuity. Quantities can be compared in terms of "more", "less", or "equal", or by assigning a numerical value multiple of a u ...
; and although much diversity existed with respect to the choice of letters, there came to be several universally recognized rules. Here thus in the history of equations the first letters of the alphabet became indicatively known as coefficients
In mathematics, a coefficient is a multiplicative factor involved in some term of a polynomial, a series, or any other type of expression. It may be a number without units, in which case it is known as a numerical factor. It may also be a ...
, while the last letters as unknown terms (an '' incerti ordinis''). In algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
, again, a similar rule was to be observed: the last letters of the alphabet came to denote the variable or current coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the Position (geometry), position of the Point (geometry), points or other geometric elements on a manifold such as ...
. Certain letters were by universal consent appropriated as symbols for the frequently occurring numbers (such as for 3.14159... and for 2.7182818...), and other uses were to be avoided as much as possible. Letters, too, were to be employed as symbols of operation, and with them other previously mentioned arbitrary operation characters. The letters and elongated S were to be appropriated as operative symbols in differential calculus
In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve. ...
and integral calculus
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Int ...
, and Delta (letter), and in the calculus of differences. In Functional (mathematics), functional notation, a letter, as a symbol of operation, is combined with another which is regarded as a symbol of Quantity#Quantity in mathematics, quantity.
Thus, denotes the mathematical result of the performance of the operation upon the Mathematical object, subject . If upon this result the same operation is repeated, the new result would be expressed by , or more concisely by , and so on. The quantity itself regarded as the result of the same operation upon some other function; the proper symbol for which is, by analogy, . Thus and are symbols of Multiplicative inverse, inverse operations, the former cancelling the effect of the latter on the subject . and in a similar manner are termed inverse functions.
Beginning in 1718, Thomas Twinin used the Slash (punctuation), division slash (Slash (punctuation), solidus), deriving it from the earlier Arabic horizontal fraction bar. Pierre-Simon Laplace, Pierre-Simon, Marquis de Laplace developed the widely used Laplace operator, Laplacian differential operator (e.g. ). In 1750, Gabriel Cramer developed Cramer's Rule for solving linear systems.
Euler and prime notations
Leonhard Euler was one of the most prolific mathematicians in history, and also a prolific inventor of canonical notation. Contributions of Leonhard Euler to mathematics, His contributions include his use of to represent the base of natural logarithms. It is not known exactly why was chosen, but it was probably because the first four letters of the alphabet were already commonly used to represent variables and other constants. Euler consistently used to represent pi. The use of was suggested by William Jones, who used it as shorthand forperimeter
A perimeter is the length of a closed boundary that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional line. The perimeter of a circle or an ellipse is called its circumference.
Calculating the perimet ...
. Euler used to represent the square root of negative one () although he earlier used it as an ''infinite number.'' Today, the symbol created by John Wallis
John Wallis (; ; ) was an English clergyman and mathematician, who is given partial credit for the development of infinitesimal calculus.
Between 1643 and 1689 Wallis served as chief cryptographer for Parliament and, later, the royal court. ...
, , is used for infinity, as in e.g. . For summation
In mathematics, summation is the addition of a sequence of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, pol ...
, Euler used an enlarged form of the upright capital Greek letter Sigma (letter), sigma (Σ), known as capital-sigma notation. This is defined as:
where ''i'' represents the index of summation; ''ai'' is an indexed variable representing each successive term in the series; ''m'' is the lower bound of summation, and ''n'' is the upper bound of summation. The term "''i = m''" under the summation symbol means that the index ''i'' starts equal to ''m''. The index, ''i'', is incremented by 1 for each successive term, stopping when ''i'' = ''n''.
For function (mathematics), functions, Euler used the notation to represent a function of .
The William Emerson (mathematician), mathematician William Emerson developed the proportionality sign (∝). Proportionality (mathematics), Proportionality is the ratio of one quantity to another, and the sign is used to indicate the ratio between two variables is constant. Much later in the abstract expressions of the value of various proportional phenomena, the parts-per notation would become useful as a set of pseudo-units to describe small values of miscellaneous Dimensionless quantity, dimensionless quantities. Marquis de Condorcet, in 1768, advanced the partial differential sign (∂), known as the ''curly d'' or ''Jacobi's delta''. The prime symbol (′) for derivatives was made by Joseph-Louis Lagrange.
Gauss, Hamilton, and matrix notations
At the turn of the 19th century, Carl Friedrich Gauss developed the Identity (mathematics), identity sign for congruence relation and, in quadratic reciprocity, the Floor and ceiling functions, integral part. Gauss developed functions of complex variables, functions of geometry, and functions for the convergence of series (mathematics), series. He devised satisfactory proofs of the fundamental theorem of algebra and the quadratic reciprocity law. Gauss developed the Gaussian elimination method of solving linear systems, which was initially listed as an advancement in geodesy. He would also develop the product sign (). In the 1800s, Christian Kramp promotedfactorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times ...
notation during his research in generalized factorial function which applied to non-integers. Joseph Diaz Gergonne introduced the set inclusion signs (⊆, ⊇), later redeveloped by Ernst Schröder (mathematician), Ernst Schröder. Peter Gustav Lejeune Dirichlet developed Dirichlet L-function, Dirichlet ''L''-functions to give the proof of Dirichlet's theorem on arithmetic progressions and began analytic number theory. In 1829, Carl Gustav Jacob Jacobi published ''Fundamenta nova theoriae functionum ellipticarum'' with his Elliptic function, elliptic theta functions.
Matrix notation would be more fully developed by Arthur Cayley in his three papers, on subjects which had been suggested by reading the ''Mécanique analytique'' of Lagrange and some of the works of Laplace. Cayley defined matrix multiplication and matrix inverses. Cayley used a single letter to denote a matrix, thus treating a matrix as an aggregate object. He also realized the connection between matrices and determinants, and wrote "There would be many things to say about this theory of matrices which should, it seems to me, precede the theory of determinants."Marie A. Vitulli, Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Originally at: darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html
William Rowan Hamilton introduced the nabla symbol ( or, later called ''del'', ∇) for vector differentials. This was previously used by Hamilton as a general-purpose Operator (mathematics), operator sign. , , and are used for the Hamiltonian (quantum mechanics), Hamiltonian operator in quantum mechanics and (or ℋ ) for the Hamiltonian function in classical Hamiltonian mechanics. In mathematics, Hamilton is perhaps best known as the inventor of Classical Hamiltonian quaternions, quaternion notation and biquaternions.
Maxwell, Clifford, and Ricci notations
 In 1864 James Clerk Maxwell reduced all of the then-current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in ''A Dynamical Theory of the Electromagnetic Field''. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.) (See Maxwell's equations.) The method of calculation that is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used, they are known as Lagrange's equations. In 1871 Richard Dedekind defined a field (mathematics), field to be a set of real or complex numbers which is closed under the four arithmetic operations. In 1873 Maxwell presented ''A Treatise on Electricity and Magnetism''.
In 1878 William Kingdon Clifford published his ''Elements of Dynamic''. Clifford developed split-biquaternions (e.g. History of quaternions, ) which he called ''algebraic motors''. Clifford obviated quaternion study by separating the
In 1864 James Clerk Maxwell reduced all of the then-current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in ''A Dynamical Theory of the Electromagnetic Field''. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.) (See Maxwell's equations.) The method of calculation that is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used, they are known as Lagrange's equations. In 1871 Richard Dedekind defined a field (mathematics), field to be a set of real or complex numbers which is closed under the four arithmetic operations. In 1873 Maxwell presented ''A Treatise on Electricity and Magnetism''.
In 1878 William Kingdon Clifford published his ''Elements of Dynamic''. Clifford developed split-biquaternions (e.g. History of quaternions, ) which he called ''algebraic motors''. Clifford obviated quaternion study by separating the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
and cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
of two vectors from the complete quaternion notation.
The common vector notations are used when working with vector (geometric), spatial vectors or more abstract members of vector spaces, while angle notation (or phasor (sine waves), phasor notation) is a notation used in electronics.
Lord Kelvin's Aether theories, aetheric atomic theory, atom theory (1860s) led Peter Guthrie Tait, in 1885, to publish a topology, topological table of knots with up to ten crossings known as the Tait conjectures. Tensor calculus was developed by Gregorio Ricci-Curbastro between 1887 and 1896, presented in 1892 under the title ''Absolute differential calculus'', and the contemporary usage of "tensor" was stated by Woldemar Voigt in 1898. In 1895, Henri Poincaré published ''Analysis Situs (paper), Analysis Situs''. In 1897, Charles Proteus Steinmetz would publish :openlibrary:books/OL7218906M/Theory and calculation of alternating current phenomena, ''Theory and Calculation of Alternating Current Phenomena'', with the assistance of Ernst J. Berg.
From formula mathematics to tensors
In 1895 Giuseppe Peano issued his ''Formulario mathematico'', an effort to digest mathematics into terse text based on special symbols. He would provide a definition of a vector space and linear map. He would also introduce the Intersection (set theory), intersection sign (), the union sign (), the Element (mathematics), membership sign (∈), and existential quantifier (∃). Peano would pass to Bertrand Russell his work in 1900 at a Paris conference; it so impressed Russell that he too was taken with the drive to render mathematics more concisely. The result was ''Principia Mathematica'' written with Alfred North Whitehead. This treatise marks a watershed in modern literature where symbol became dominant. Peano's ''Formulario Mathematico'', though less popular than Russell's work, continued through five editions. The fifth appeared in 1908 and included 4,200 formulas and theorems. Ricci-Curbastro and Tullio Levi-Civita popularized the tensor index notation around 1900.Mathematical logic and abstraction
Georg Cantor introduced Aleph numbers, so named because they use the aleph symbol (א) with natural number subscripts to denote cardinality in infinite sets. For the ordinals he employed the Greek letter ω (omega). This notation is still in use today in ordinal notation of a finite sequence of symbols from a finite alphabet that names an ordinal number according to some scheme which gives meaning to the language. After the turn of the 20th century, Josiah Willard Gibbs introduced into physical chemistry the middle dot fordot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
and the multiplication sign for cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
s. He also supplied notation for the scalar and vector products, which were introduced in ''Vector Analysis (Gibbs/Wilson), Vector Analysis''. Bertrand Russell shortly afterward introduced logical disjunction (or) in 1906. Gerhard Kowalewski and Cuthbert Edmund Cullis introduced and helped standardized matrices notation, and parenthetical matrix and box matrix notation, respectively.
 Albert Einstein, in 1916, introduced Einstein notation, which summed over a set of index notation, indexed terms in a formula, thus exerting notational brevity. For example, for indices ranging over the Set (mathematics), set ,
:
is reduced by convention to:
:
Albert Einstein, in 1916, introduced Einstein notation, which summed over a set of index notation, indexed terms in a formula, thus exerting notational brevity. For example, for indices ranging over the Set (mathematics), set ,
:
is reduced by convention to:
:Upper indices are not Exponentiation, exponents but are indices of coordinates,
coefficient
In mathematics, a coefficient is a Factor (arithmetic), multiplicative factor involved in some Summand, term of a polynomial, a series (mathematics), series, or any other type of expression (mathematics), expression. It may be a Dimensionless qu ...
s, or basis vectors.
In 1917 Arnold Sommerfeld created the contour integral sign, and Dimitry Mirimanoff proposed the axiom of regularity. In 1919, Theodor Kaluza would solve general relativity equations using Five-dimensional space, five dimensions, the results would have electromagnetic equations emerge. This would be published in 1921 in "Zum Unitätsproblem der Physik". In 1922, Abraham Fraenkel and Thoralf Skolem independently proposed replacing the axiom schema of specification with the axiom schema of replacement. Also in 1922, Zermelo–Fraenkel set theory was developed. In 1923, Steinmetz would publis''Four Lectures on Relativity and Space''
Around 1924, Jan Arnoldus Schouten developed the modern notation and formalism for the Ricci calculus framework during the absolute differential calculus applications to general relativity and differential geometry in the early twentieth century. Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields. In 1925, Enrico Fermi described a Fermi–Dirac statistics, system comprising many identical particles that obey the Pauli exclusion principle, afterwards developing a diffusion equation (Fermi age equation). In 1926, Oskar Klein develop the Kaluza–Klein theory. In 1928, Emil Artin abstracted ring theory with Artinian rings. In 1933, Andrey Kolmogorov introduces the Kolmogorov axioms. In 1937, Bruno de Finetti deduced the "Coherence (philosophical gambling strategy), operational subjective" concept.
Mathematical symbolism
Mathematical abstraction began as a process of extracting the underlying essence of a mathematical concept, removing any dependence on real world objects with which it might originally have been connected, and generalizing it so that it has wider applications or matching among other abstract descriptions of equivalent phenomena. Two abstract areas of modern mathematics are category theory and model theory. Bertrand Russell once said, "Ordinary language is totally unsuited for expressing what physics really asserts, since the words of everyday life are not sufficiently abstract. Only mathematics and mathematical logic can say as little as the physicist means to say." Though, one can substitute mathematics for real world objects, and wander off through equation after equation, and can build a concept structure which has no relation to reality. Some of the introduced mathematical logic notation during this time included the set of symbols used in Boolean algebra (logic), Boolean algebra. This was created by George Boole in 1854. Boole himself did not see logic as a branch of mathematics, but it has come to be encompassed anyway. Symbols found in Boolean algebra include (and), (or), and (not). With these symbols, and letters to represent different truth values, one can make logical statements such as , that is "(''a'' is true or ''a'' is not true) is true", meaning it is true that ''a'' is either true or not true (i.e. false). Boolean algebra has many practical uses as it is, but it also was the start of what would be a large set of symbols to be used in logic. Most of these symbols can be found in propositional calculus, a formal system described as . is the set of elements, such as the ''a'' in the example with Boolean algebra above. is the set that contains the subsets that contain operations, such as or . contains the inference rules, which are the rules dictating how inferences may be logically made, and contains the axioms. Predicate logic, originally called ''predicate calculus'', expands on propositional logic by the introduction of Variable (mathematics), variables, usually denoted by ''x'', ''y'', ''z'', or other lowercase letters, and by sentences containing variables, called Predicate (mathematical logic), predicates. These are usually denoted by an uppercase letter followed by a list of variables, such as P(''x'') or Q(''y'',''z''). Predicate logic uses special symbols for Quantifiers (logic), quantifiers: ∃ for "there exists" and ∀ for "for all".Gödel incompleteness notation
While proving Gödel's incompleteness theorems, his incompleteness theorems, Kurt Gödel created an alternative to the symbols normally used in logic. He used Gödel numbers—numbers assigned to represent mathematical operations—and variables with the prime numbers greater than 10. With Gödel numbers, a logic statement can be broken down into a number sequence. By taking the ''n'' prime numbers to the power of the Gödel numbers in the sequence, and then multiplying the terms together, a unique final product is generated. In this way, every logic statement can be encoded as its own number. For example, take the statement "There exists a number ''x'' such that it is not ''y''". Using the symbols of propositional calculus, this would become :. If the Gödel numbers replace the symbols, it becomes: :. There are ten numbers, so the first ten prime numbers are used: :. Then, each prime is raised to the power of the corresponding Gödel number, and multiplied: :. The resulting number is approximately .Contemporary notation and topics
Early 20th-century notation
The abstraction of notation is an ongoing process. The historical development of many mathematical topics exhibits a progression from the concrete to the abstract. Throughout 20th century, various set notations were developed for fundamental object Set (mathematics), sets. Around 1924, David Hilbert and Richard Courant published ''Methoden der mathematischen Physik, Methods of mathematical physics. Partial differential equations''. In 1926, Oskar Klein and Walter Gordon (physicist), Walter Gordon proposed the Klein–Gordon equation to describe relativistic particles: The first formulation of a quantum mechanics, quantum theory describing radiation and matter interaction is due to Paul Adrien Maurice Dirac, who, during 1920, was first able to compute the coefficient of spontaneous emission of an atom. In 1928, the relativistic wave equation, relativistic Dirac equation was formulated by Dirac to explain the behavior of the relativistically moving electron. The Dirac equation in the form originally proposed by Dirac is: where, is the wave function for the electron, and are the space and time coordinates, is the rest mass of the electron, is the momentum (understood to be the momentum operator in the Schrödinger equation, Schrödinger theory), is the speed of light, and is the reduced Planck constant. Dirac described the quantification of the electromagnetic field as an ensemble of harmonic oscillators with the introduction of the concept of creation and annihilation operators of particles. In the following years, with contributions from Wolfgang Pauli, Eugene Wigner, Pascual Jordan, and Werner Heisenberg, and an elegant formulation of quantum electrodynamics due to Enrico Fermi, physicists came to believe that, in principle, it would be possible to perform any computation for any physical process involving photons and charged particles. In 1931, Alexandru Proca developed the Proca equation (Euler–Lagrange equation) for the vector meson theory of nuclear forces and the relativistic quantum field equations. John Archibald Wheeler in 1937 developed the S-matrix. Studies by Felix Bloch with Arnold Nordsieck, and Victor Weisskopf, in 1937 and 1939, revealed that such computations were reliable only at a first order of Perturbation theory (quantum mechanics), perturbation theory, a problem already pointed out by Robert Oppenheimer. Infinities emerged at higher orders in the series, making such computations meaningless and casting serious doubts on the internal consistency of the theory itself. With no solution for this problem known at the time, it appeared that a fundamental incompatibility existed between special relativity and quantum mechanics. In the 1930s, the double-struck capital Z () for integer number sets was created by Edmund Landau. Nicolas Bourbaki created the double-struck capital Q () for rational number sets. In 1935 Gerhard Gentzen made universal quantifiers. André Weil and Nicolas Bourbaki would develop the empty set sign (∅) in 1939. That same year, Nathan Jacobson would coin the double-struck capital C () for complex number sets. Around the 1930s, Voigt notation (so named to honor Voigt's 1898 work) would be developed for multilinear algebra as a way to represent a symmetric tensor by reducing its order. Schoenflies notation, Schönflies notation became one of two conventions used to describe point groups (the other being Hermann–Mauguin notation). Also in this time, van der Waerden notation became popular for the usage of two-component spinors (Weyl spinors) in four spacetime dimensions. Arend Heyting would introduce Heyting algebra and Heyting arithmetic. The arrow (→) was developed for function notation in 1936 by Øystein Ore to denote images of specific elements and to denote Galois connections. Later, in 1940, it took its present form (''f: X→Y'') through the work of Witold Hurewicz. Werner Heisenberg, in 1941, proposed the S-matrix theory of particle interactions.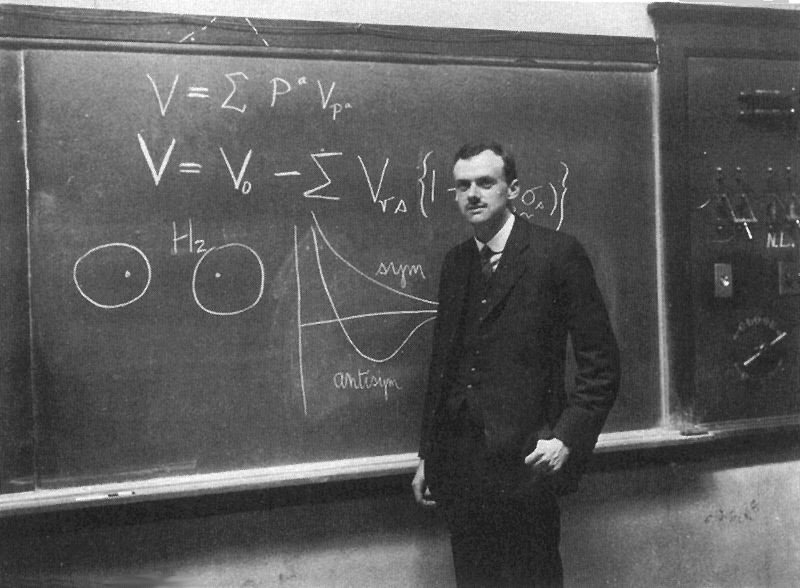 Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of bracket, angle brackets and vertical bars. It can also be used to denote abstract vector space, vectors and linear functionals. It is so called because the inner product (or
Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of bracket, angle brackets and vertical bars. It can also be used to denote abstract vector space, vectors and linear functionals. It is so called because the inner product (or dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
on a complex vector space) of two states is denoted by a bra, ket: . The notation was introduced in 1939 by Paul Dirac,
though the notation has precursors in Hermann Grassmann, Grassmann's use of the notation [''φ'', ''ψ''] for his inner products nearly 100 years previously.
Bra–ket notation is widespread in quantum mechanics: almost every phenomenon that is explained using quantum mechanics—including a large portion of modern physics—is usually explained with the help of bra–ket notation. The notation establishes an encoded abstract representation-independence, producing a versatile specific representation (e.g., ''x'', or ''p'', or eigenfunction base) without much ado, or excessive reliance on, the Nature (philosophy), nature of the linear spaces involved. The overlap expression ⟨''φ'', ''ψ''⟩ is typically interpreted as the probability amplitude for the Quantum state, state ''ψ'' to wavefunction collapse, collapse into the state ''Φ#Use as a symbol, ϕ''. The Feynman slash notation (Dirac slash notation) was developed by Richard Feynman for the study of Dirac fields in quantum field theory.
Geoffrey Chew, along with others, would promote matrix notation for the strong interaction in particle physics, and the associated Bootstrapping (physics), bootstrap principle, in 1960. In the 1960s, set-builder notation was developed for describing a Set (mathematics), set by stating the properties that its members must satisfy. Also in the 1960s, tensors are abstracted within category theory by means of the concept of monoidal category. Later, multi-index notation eliminates conventional notions used in multivariable calculus, partial differential equations, and the theory of distribution (mathematics), distributions, by abstracting the concept of an integer index notation, index to an ordered tuple of indices.
Modern mathematical notation
In the modern mathematics of special relativity, electromagnetism, and Wave, wave theory, the d'Alembert operator () is the Laplace operator of Minkowski space. The Levi-Civita symbol (), also known as the permutation symbol, is used in tensor calculus. Feynman diagrams are used in particle physics, equivalent to the Operator (physics), operator-based approach of Sin-Itiro Tomonaga and Julian Schwinger. The orbifold notation system, invented by William Thurston, has been developed for representing types of symmetry groups in two-dimensional spaces of constant curvature. The tetrad formalism (tetrad (index notation), tetrad index notation) was introduced as an approach to general relativity that replaces the choice of a coordinate basis by the less restrictive choice of a local basis for the tangent bundle (a locally defined set of four linearly independent vector fields called a Tetrad (general relativity), tetrad). In the 1990s, Roger Penrose proposed Penrose graphical notation (tensor diagram notation) as a, usually handwritten, visual depiction of multilinear functions or tensors. Penrose also introduced abstract index notation. His usage of the Einstein summation was in order to offset the inconvenience in describing tensor contraction, contractions and covariant derivative, covariant differentiation in modern abstract tensor notation, while maintaining explicit covariance of the expressions involved. John Horton Conway, John Conway furthered various notations, including the Conway chained arrow notation, the Conway notation (knot theory), Conway notation of knot theory, and the Conway polyhedron notation. The Coxeter notation system classifies symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter; Norman Johnson (mathematician), Norman Johnson more comprehensively defined it. Combinatorics, Combinatorial LCF notation, devised by Joshua Lederberg and extended by Harold Scott MacDonald Coxeter and Robert Frucht, was developed for the representation of cubic graphs that are Hamiltonian path, Hamiltonian. The cycle notation is the convention for writing down a permutation in terms of its constituent cyclic permutation, cycles. This is also called circular notation and the permutation called a ''cyclic'' or ''circular'' permutation.Computers and markup notation
In 1931, IBM produces the List of IBM products, IBM 601 Multiplying Punch; it is an electromechanical machine that could read two numbers, up to eight digits long, from a card and punch their product onto the same card. In 1934, Wallace Eckert used a rigged IBM 601 Multiplying Punch to automate the integration of differential equations. In 1962, Kenneth E. Iverson developed an integral part notation, which became known as Iverson notation, that developed into APL (programming language), APL. In the 1970s within computer architecture, Quote notation was developed for a representing number system of rational numbers. Also in this decade, the Z notation (just like the APL (programming language), APL language, long before it) uses many non-ASCII symbols, the specification includes suggestions for rendering the Z notation symbols in ASCII and in LaTeX. There are presently various C mathematical functions (Math.h) and numerical Library (computing), libraries used to perform numerical analysis, numerical calculations in software development. These calculations can be handled by symbolic executions—analyzing a program to determine what inputs cause each part of a program to execute. Mathematica and SymPy are examples of computational software programs based on symbolic mathematics.References and citations
;General *Florian Cajori (1929) ''A History of Mathematical Notations'', 2 vols. Dover reprint in 1 vol., 1993. . ;CitationsFurther reading
;General:A Short Account of the History of Mathematics
By Walter William Rouse Ball.
A Primer of the History of Mathematics
By Walter William Rouse Ball.
A History of Elementary Mathematics
With Hints on Methods of Teaching. By Florian Cajori.
A History of Elementary Mathematics
By Florian Cajori.
A History of Mathematics
By Florian Cajori.
A Short History of Greek Mathematics
By James Gow (scholar), James Gow.
On the Development of Mathematical Thought During the Nineteenth Century
By John Theodore Merz.
A New Mathematical and Philosophical Dictionary
By Peter Barlow.
Historical Introduction to Mathematical Literature
By George Abram Miller
A Brief History of Mathematics
By Karl Fink, Wooster Woodruff Beman, David Eugene Smith
History of Modern Mathematics
By David Eugene Smith.
History of modern mathematics
By David Eugene Smith, Mansfield Merriman. ;Other * Principia Mathematica
Volume 1
Volume 2
By Alfred North Whitehead, Bertrand Russell.
The Mathematical Principles of Natural Philosophy
Volume 1, Issue 1. By Sir Isaac Newton, Andrew Motte, William Davis, John Machin, William Emerson.
General investigations of curved surfaces of 1827 and 1825
By Carl Friedrich Gaus.
External links
Mathematical Notation: Past and Future
files.chem.vt.edu.
Some Common Mathematical Symbols and Abbreviations (with History)
Isaiah Lankham, Bruno Nachtergaele, Anne Schilling. {{History of mathematics History of mathematics, Mathematical notation Mathematical notation Articles which contain graphical timelines