Hill Kinetics on:
[Wikipedia]
[Google]
[Amazon]
 In
In
/chem>is the total
A is the ligand, equivalent to L, and R is the receptor. can be expressed in terms of the total amount of receptor and ligand-bound receptor concentrations: . is equal to the ratio of the dissociation rate of the ligand-receptor complex to its association rate (). Kd is the equilibrium constant for dissociation. is defined so that , this is also known as the microscopic
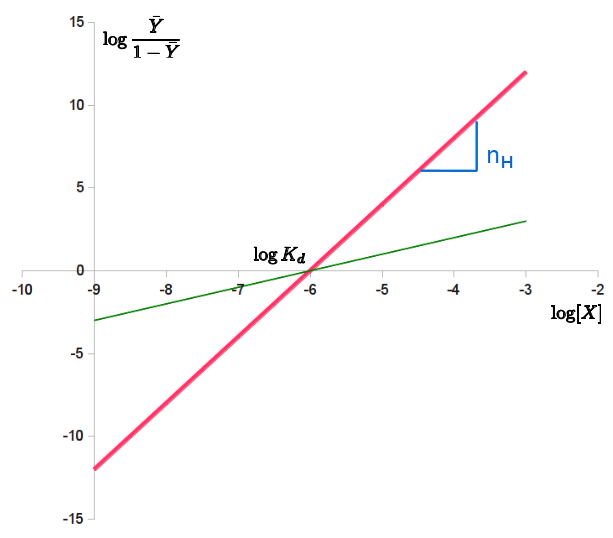 The Hill plot is the rearrangement of the Hill equation into a straight line.
Taking the reciprocal of both sides of the Hill equation, rearranging, and inverting again yields: . Taking the logarithm of both sides of the equation leads to an alternative formulation of the Hill-Langmuir equation:
:.
This last form of the Hill equation is advantageous because a plot of versus yields a linear plot, which is called a Hill plot. Because the slope of a Hill plot is equal to the Hill coefficient for the biochemical interaction, the slope is denoted by . A slope greater than one thus indicates positively cooperative binding between the receptor and the ligand, while a slope less than one indicates negatively cooperative binding.
Transformations of equations into linear forms such as this were very useful before the widespread use of computers, as they allowed researchers to determine parameters by fitting lines to data. However, these transformations affect error propagation, and this may result in undue weight to error in data points near 0 or 1. This impacts the parameters of linear regression lines fitted to the data. Furthermore, the use of computers enables more robust analysis involving
The Hill plot is the rearrangement of the Hill equation into a straight line.
Taking the reciprocal of both sides of the Hill equation, rearranging, and inverting again yields: . Taking the logarithm of both sides of the equation leads to an alternative formulation of the Hill-Langmuir equation:
:.
This last form of the Hill equation is advantageous because a plot of versus yields a linear plot, which is called a Hill plot. Because the slope of a Hill plot is equal to the Hill coefficient for the biochemical interaction, the slope is denoted by . A slope greater than one thus indicates positively cooperative binding between the receptor and the ligand, while a slope less than one indicates negatively cooperative binding.
Transformations of equations into linear forms such as this were very useful before the widespread use of computers, as they allowed researchers to determine parameters by fitting lines to data. However, these transformations affect error propagation, and this may result in undue weight to error in data points near 0 or 1. This impacts the parameters of linear regression lines fitted to the data. Furthermore, the use of computers enables more robust analysis involving
 A distinction should be made between quantification of drugs binding to receptors and drugs producing responses. There may not necessarily be a linear relationship between the two values. In contrast to this article's previous definition of the Hill equation, the
A distinction should be made between quantification of drugs binding to receptors and drugs producing responses. There may not necessarily be a linear relationship between the two values. In contrast to this article's previous definition of the Hill equation, the /chem> is the drug concentration, is the Hill coefficient, and is the drug concentration that produces a 50% maximal response. Dissociation constants (in the previous section) relate to ligand binding, while reflects tissue response.
This form of the equation can reflect tissue/cell/population responses to drugs and can be used to generate
EC90 and EC10 are the input values needed to produce the 10% and 90% of the maximal response, respectively.
Hill equation calculator
{{DEFAULTSORT:Hill Equation Enzyme kinetics Pharmacology
biochemistry
Biochemistry, or biological chemistry, is the study of chemical processes within and relating to living organisms. A sub-discipline of both chemistry and biology, biochemistry may be divided into three fields: structural biology, enzymology, a ...
and pharmacology
Pharmacology is the science of drugs and medications, including a substance's origin, composition, pharmacokinetics, pharmacodynamics, therapeutic use, and toxicology. More specifically, it is the study of the interactions that occur betwee ...
, the Hill equation refers to two closely related equations that reflect the binding of ligands
In coordination chemistry, a ligand is an ion or molecule with a functional group that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's ...
to macromolecules, as a function of the ligand concentration
In chemistry, concentration is the abundance of a constituent divided by the total volume of a mixture. Several types of mathematical description can be distinguished: '' mass concentration'', '' molar concentration'', '' number concentration'', ...
. A ligand
In coordination chemistry, a ligand is an ion or molecule with a functional group that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's el ...
is "a substance that forms a complex with a biomolecule to serve a biological purpose", and a macromolecule
A macromolecule is a "molecule of high relative molecular mass, the structure of which essentially comprises the multiple repetition of units derived, actually or conceptually, from molecules of low relative molecular mass." Polymers are physi ...
is a very large molecule, such as a protein, with a complex structure of components. Protein-ligand binding typically changes the structure of the target protein, thereby changing its function in a cell.
The distinction between the two Hill equations is whether they measure ''occupancy'' or ''response''. The Hill equation reflects the occupancy of macromolecules: the fraction that is saturated or bound by the ligand
In coordination chemistry, a ligand is an ion or molecule with a functional group that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's el ...
.For clarity, this article will use the International Union of Basic and Clinical Pharmacology
The International Union of Basic and Clinical Pharmacology (IUPHAR) is a voluntary, non-profit association representing the interests of scientists in pharmacology-related fields to facilitate ''Better Medicines through Global Education and Resea ...
convention of distinguishing between the Hill-Langmuir equation (for receptor saturation) and Hill equation (for tissue response) This equation is formally equivalent to the Langmuir isotherm
The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressu ...
. Conversely, the Hill equation proper reflects the cellular or tissue response to the ligand: the physiological output of the system, such as muscle contraction.
The Hill equation was originally formulated by Archibald Hill
Archibald Vivian Hill (26 September 1886 – 3 June 1977), better known to friends and colleagues as A. V. Hill, was a British physiologist, one of the founders of the diverse disciplines of biophysics and operations research. He shared the 192 ...
in 1910 to describe the sigmoidal O2 binding curve of hemoglobin
Hemoglobin (haemoglobin, Hb or Hgb) is a protein containing iron that facilitates the transportation of oxygen in red blood cells. Almost all vertebrates contain hemoglobin, with the sole exception of the fish family Channichthyidae. Hemoglobin ...
.
The binding of a ligand
In coordination chemistry, a ligand is an ion or molecule with a functional group that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's el ...
to a macromolecule
A macromolecule is a "molecule of high relative molecular mass, the structure of which essentially comprises the multiple repetition of units derived, actually or conceptually, from molecules of low relative molecular mass." Polymers are physi ...
is often enhanced if there are already other ligands present on the same macromolecule (this is known as cooperative binding
Cooperative binding occurs in molecular binding systems containing more than one type, or species, of molecule and in which one of the partners is not mono-valent and can bind more than one molecule of the other species. In general, molecular bindi ...
). The Hill equation is useful for determining the degree of cooperativity
Cooperativity is a phenomenon displayed by systems involving identical or near-identical elements, which act dependently of each other, relative to a hypothetical standard non-interacting system in which the individual elements are acting indepen ...
of the ligand(s) binding to the enzyme or receptor. The Hill coefficient provides a way to quantify the degree of interaction between ligand binding sites.
The Hill equation (for response) is important in the construction of dose-response curves.
Proportion of ligand-bound receptors
The Hill equation is commonly expressed in the following ways: :, where * is the fraction of the receptor protein concentration that is bound by theligand
In coordination chemistry, a ligand is an ion or molecule with a functional group that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's el ...
,
*ligand
In coordination chemistry, a ligand is an ion or molecule with a functional group that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's el ...
concentration,
* is the apparent dissociation constant
In chemistry, biochemistry, and pharmacology, a dissociation constant (''K''D) is a specific type of equilibrium constant that measures the propensity of a larger object to separate (dissociate) reversibly into smaller components, as when a complex ...
derived from the law of mass action
In chemistry, the law of mass action is the proposition that the rate of a chemical reaction is directly proportional to the product of the activities or concentrations of the reactants. It explains and predicts behaviors of solutions in dy ...
,
* is the ligand concentration producing half occupation,
* is the Hill coefficient.
The special case where is a Monod equation
The Monod equation is a mathematical model for the growth of microorganisms. It is named for Jacques Monod (1910–1976, a French biochemist, Nobel Prize in Physiology or Medicine in 1965), who proposed using an equation of this form to relate micr ...
.
Constants
In pharmacology, is often written as , wheredissociation constant
In chemistry, biochemistry, and pharmacology, a dissociation constant (''K''D) is a specific type of equilibrium constant that measures the propensity of a larger object to separate (dissociate) reversibly into smaller components, as when a complex ...
and is the ligand concentration occupying half of the binding sites. In recent literature, this constant is sometimes referred to as .
Gaddum equation
The Gaddum equation is a further generalisation of the Hill-equation, incorporating the presence of a reversible competitive antagonist. The Gaddum equation is derived similarly to the Hill-equation but with 2 equilibria: both the ligand with the receptor and the antagonist with the receptor. Hence, the Gaddum equation has 2 constants: the equilibrium constants of the ligand and that of the antagonistHill plot
 The Hill plot is the rearrangement of the Hill equation into a straight line.
Taking the reciprocal of both sides of the Hill equation, rearranging, and inverting again yields: . Taking the logarithm of both sides of the equation leads to an alternative formulation of the Hill-Langmuir equation:
:.
This last form of the Hill equation is advantageous because a plot of versus yields a linear plot, which is called a Hill plot. Because the slope of a Hill plot is equal to the Hill coefficient for the biochemical interaction, the slope is denoted by . A slope greater than one thus indicates positively cooperative binding between the receptor and the ligand, while a slope less than one indicates negatively cooperative binding.
Transformations of equations into linear forms such as this were very useful before the widespread use of computers, as they allowed researchers to determine parameters by fitting lines to data. However, these transformations affect error propagation, and this may result in undue weight to error in data points near 0 or 1. This impacts the parameters of linear regression lines fitted to the data. Furthermore, the use of computers enables more robust analysis involving
The Hill plot is the rearrangement of the Hill equation into a straight line.
Taking the reciprocal of both sides of the Hill equation, rearranging, and inverting again yields: . Taking the logarithm of both sides of the equation leads to an alternative formulation of the Hill-Langmuir equation:
:.
This last form of the Hill equation is advantageous because a plot of versus yields a linear plot, which is called a Hill plot. Because the slope of a Hill plot is equal to the Hill coefficient for the biochemical interaction, the slope is denoted by . A slope greater than one thus indicates positively cooperative binding between the receptor and the ligand, while a slope less than one indicates negatively cooperative binding.
Transformations of equations into linear forms such as this were very useful before the widespread use of computers, as they allowed researchers to determine parameters by fitting lines to data. However, these transformations affect error propagation, and this may result in undue weight to error in data points near 0 or 1. This impacts the parameters of linear regression lines fitted to the data. Furthermore, the use of computers enables more robust analysis involving nonlinear regression
In statistics, nonlinear regression is a form of regression analysis in which observational data are modeled by a function which is a nonlinear combination of the model parameters and depends on one or more independent variables. The data are fi ...
.
Tissue response
 A distinction should be made between quantification of drugs binding to receptors and drugs producing responses. There may not necessarily be a linear relationship between the two values. In contrast to this article's previous definition of the Hill equation, the
A distinction should be made between quantification of drugs binding to receptors and drugs producing responses. There may not necessarily be a linear relationship between the two values. In contrast to this article's previous definition of the Hill equation, the IUPHAR
The International Union of Basic and Clinical Pharmacology (IUPHAR) is a voluntary, non-profit association representing the interests of scientists in pharmacology-related fields to facilitate ''Better Medicines through Global Education and Resea ...
defines the Hill equation in terms of the tissue response , as
where dose response curves
Dose or Dosage may refer to:
Music
* ''Dose'' (Gov't Mule album), 1998
* ''Dose'' (Latin Playboys album)
* ''Dosage'' (album), by the band Collective Soul
* "Dose" (song), a 2018 song by Ciara
* "Dose", song by Filter from the album '' Short ...
. The relationship between and EC50 may be quite complex as a biological response will be the sum of myriad factors; a drug will have a different biological effect if more receptors are present, regardless of its affinity.
The Del-Castillo Katz model is used to relate the Hill equation to receptor activation by including a second equilibrium of the ligand-bound receptor to an ''activated'' form of the ligand-bound receptor.
Statistical analysis of response as a function of stimulus may be performed by regression methods such as the probit model
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to es ...
or logit model
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations.
Mathematically, the logit is the ...
, or other methods such as the Spearman–Kärber method. Empirical models based on nonlinear regression are usually preferred over the use of some transformation of the data that linearizes the dose-response relationship.
Hill coefficient
The Hill coefficient is a measure ofultrasensitivity
In molecular biology, ultrasensitivity describes an output response that is more sensitive to stimulus change than the hyperbolic Michaelis–Menten kinetics, Michaelis-Menten response. Ultrasensitivity is one of the biochemical switches in the cel ...
(i.e. how steep is the response curve).
The Hill coefficient, or , may describe cooperativity (or possibly other biochemical properties, depending on the context in which the Hill equation is being used). When appropriate, the value of the Hill coefficient describes the cooperativity of ligand binding in the following way:
*. Positively cooperative binding: Once one ligand molecule is bound to the enzyme, its affinity for other ligand molecules increases. For example, the Hill coefficient of oxygen binding to haemoglobin
Hemoglobin (haemoglobin, Hb or Hgb) is a protein containing iron that facilitates the transportation of oxygen in red blood cells. Almost all vertebrates contain hemoglobin, with the sole exception of the fish family Channichthyidae. Hemoglobi ...
(an example of positive cooperativity) falls within the range of 1.7–3.2.
*. Negatively cooperative binding: Once one ligand molecule is bound to the enzyme, its affinity for other ligand molecules decreases.
*. Noncooperative (completely independent) binding: The affinity of the enzyme for a ligand molecule is not dependent on whether or not other ligand molecules are already bound. When n=1, we obtain a model that can be modeled by Michaelis–Menten kinetics
In biochemistry, Michaelis–Menten kinetics, named after Leonor Michaelis and Maud Menten, is the simplest case of enzyme kinetics, applied to enzyme-catalysed reactions involving the transformation of one substrate into one product. It takes th ...
, in which , the Michaelis–Menten constant.
The Hill coefficient can be calculated approximately in terms of the ''cooperativity index'' of Taketa and Pogell as follows:
:.
where Reversible form
The most common form of the Hill equation is its irreversible form. However, when building computational models a reversible form is often required in order to model product inhibition. For this reason, Hofmeyr and Cornish-Bowden devised the reversible Hill equation.Relationship to the elasticity coefficients
The Hill coefficient is also intimately connected to theelasticity coefficient
In chemistry, the Reaction rate, rate of a chemical reaction is influenced by many different factors, such as temperature, pH, reactant, the concentration of Product (chemistry), products, and other effectors. The degree to which these factors c ...
where the Hill coefficient can be shown to equal:
where is the fractional saturation, , and the elasticity coefficient.
This is derived by taking the slope of the Hill equation:
and expanding the slope using the quotient rule. The result shows that the elasticity can never exceed since the equation above can be rearranged to:
Applications
The Hill equation is used extensively in pharmacology to quantify the functional parameters of a drug and are also used in other areas of biochemistry. The Hill equation can be used to describe dose-response relationships, for exampleion channel
Ion channels are pore-forming membrane proteins that allow ions to pass through the channel pore. Their functions include establishing a resting membrane potential, shaping action potentials and other electrical signals by Gating (electrophysiol ...
open-probability (P-open) vs. ligand concentration.
Regulation of gene transcription
The Hill equation can be applied in modelling the rate at which a gene product is produced when its parent gene is being regulated bytranscription factor
In molecular biology, a transcription factor (TF) (or sequence-specific DNA-binding factor) is a protein that controls the rate of transcription (genetics), transcription of genetics, genetic information from DNA to messenger RNA, by binding t ...
s (e.g., activators and/or repressor
In molecular genetics, a repressor is a DNA- or RNA-binding protein that inhibits the expression of one or more genes by binding to the operator or associated silencers. A DNA-binding repressor blocks the attachment of RNA polymerase to the ...
s). Doing so is appropriate when a gene is regulated by multiple binding sites for transcription factors, in which case the transcription factors may bind the DNA in a cooperative fashion.
If the production of protein from gene is up-regulated (activated) by a transcription factor , then the rate of production of protein can be modeled as a differential equation in terms of the concentration of activated protein:
:,
where is the maximal transcription rate of gene .
Likewise, if the production of protein from gene is down-regulated (repressed) by a transcription factor , then the rate of production of protein can be modeled as a differential equation in terms of the concentration of activated protein:
:,
where is the maximal transcription rate of gene .
Limitations
Because of its assumption that ligand molecules bind to a receptor simultaneously, the Hill equation has been criticized as a physically unrealistic model. Moreover, the Hill coefficient should not be considered a reliable approximation of the number of cooperative ligand binding sites on a receptor except when the binding of the first and subsequent ligands results in extreme positive cooperativity. Unlike more complex models, the relatively simple Hill equation provides little insight into underlying physiological mechanisms of protein-ligand interactions. This simplicity, however, is what makes the Hill equation a useful empirical model, since its use requires little ''a priori'' knowledge about the properties of either the protein or ligand being studied. Nevertheless, other, more complex models of cooperative binding have been proposed. For more information and examples of such models, seeCooperative binding
Cooperative binding occurs in molecular binding systems containing more than one type, or species, of molecule and in which one of the partners is not mono-valent and can bind more than one molecule of the other species. In general, molecular bindi ...
.
Global sensitivity measure such as Hill coefficient do not characterise the local behaviours of the s-shaped curves. Instead, these features are well captured by the response coefficient measure.
There is a link between Hill Coefficient and Response coefficient, as follows. Altszyler et al. (2017) have shown that these ultrasensitivity measures can be linked.
See also
*Binding coefficient In medicinal chemistry and pharmacology, a binding coefficient is a quantity representing the extent to which a chemical compound will bind to a macromolecule. The preferential binding coefficient can be derived from the Kirkwood-Buff solution theo ...
* Bjerrum plot
A Bjerrum plot (named after Niels Bjerrum), sometimes also known as a Sillén diagram (after Lars Gunnar Sillén), or a Hägg diagram (after Gunnar Hägg) is a graph of the concentrations of the different species of a polyprotic acid in a solu ...
* Cooperative binding
Cooperative binding occurs in molecular binding systems containing more than one type, or species, of molecule and in which one of the partners is not mono-valent and can bind more than one molecule of the other species. In general, molecular bindi ...
* Gompertz curve
The Gompertz curve or Gompertz function is a type of mathematical model for a time series, named after Benjamin Gompertz (1779–1865). It is a sigmoid function which describes growth as being slowest at the start and end of a given time period. T ...
* Langmuir adsorption model
The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressu ...
* Logistic function
A logistic function or logistic curve is a common S-shaped curve ( sigmoid curve) with the equation
f(x) = \frac
where
The logistic function has domain the real numbers, the limit as x \to -\infty is 0, and the limit as x \to +\infty is L.
...
* Michaelis–Menten kinetics
In biochemistry, Michaelis–Menten kinetics, named after Leonor Michaelis and Maud Menten, is the simplest case of enzyme kinetics, applied to enzyme-catalysed reactions involving the transformation of one substrate into one product. It takes th ...
* Monod equation
The Monod equation is a mathematical model for the growth of microorganisms. It is named for Jacques Monod (1910–1976, a French biochemist, Nobel Prize in Physiology or Medicine in 1965), who proposed using an equation of this form to relate micr ...
Notes
References
Further reading
* ''Dorland's Illustrated Medical Dictionary
''Dorland's'' is the brand name of a family of medical reference works (including dictionaries, spellers and word books, and spell-check software) in various media spanning printed books, CD-ROMs, and online content. The flagship products are ''Do ...
''
*
*
*
*
*
*
*
*
*
*
*
External links
Hill equation calculator
{{DEFAULTSORT:Hill Equation Enzyme kinetics Pharmacology