Hardy Cross Method

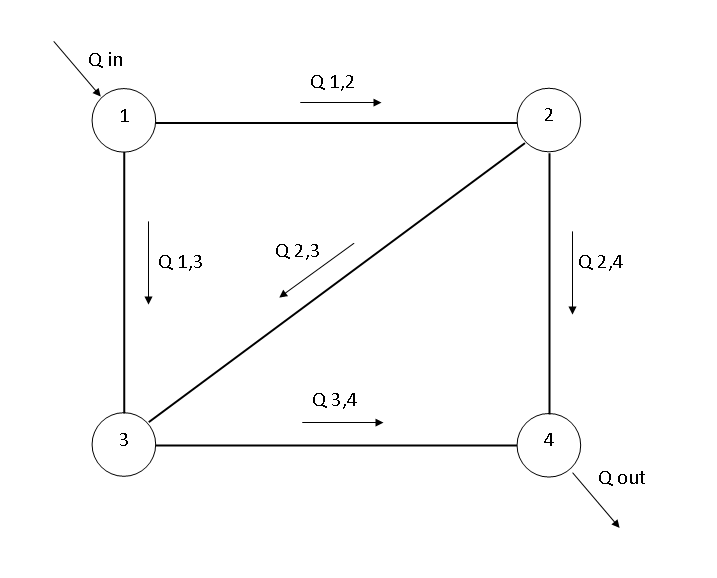
The Hardy Cross method is an iterative method for determining the flow in pipe network systems where the inputs and outputs are known, but the flow inside the network is unknown.
The method was first published in November 1936 by its namesake, Hardy Cross, a structural engineering professor at the University of Illinois at Urbana–Champaign. The Hardy Cross method is an adaptation of the Moment distribution method, which was also developed by Hardy Cross as a way to determine the forces in statically indeterminate structures.

The introduction of the Hardy Cross method for analyzing pipe flow networks revolutionized municipal water supply design. Before the method was introduced, solving complex pipe systems for distribution was extremely difficult due to the nonlinear relationship between head loss and flow. The method was later made obsolete by computer solving algorithms employing the Newton–Raphson method or other numerical methods that eliminate the need to solve nonlinear systems of equations by hand.

History

In 1930, Hardy Cross published a paper called "Analysis of Continuous Frames by Distributing Fixed-End Moments" in which he described the moment distribution method, which would change the way engineers in the field performed structural analysis. The moment distribution method was used to determine the forces in statically indeterminate structures and allowed for engineers to safely design structures from the 1930s through the 1960s, until the development of computer oriented methods. In November 1936, Cross applied the same geometric method to solving pipe network flow distribution problems, and published a paper called "Analysis of flow in networks of conduits or conductors."

Derivation

The Hardy Cross method is an application of continuity of flow and continuity of potential to iteratively solve for flows in a pipe network. In the case of pipe flow, conservation of flow means that the flow in is equal to the flow out at each junction in the pipe. Conservation of potential means that the total directional head loss along any loop in the system is zero (assuming that a head loss counted against the flow is actually a head gain).

Hardy Cross developed two methods for solving flow networks. Each method starts by maintaining either continuity of flow or potential, and then iteratively solves for the other.

Assumptions

The Hardy Cross method assumes that the flow going in and out of the system is known and that the pipe length, diameter, roughness and other key characteristics are also known or can be assumed. The method also assumes that the relation between flow rate and head loss is known, but the method does not require any particular relation to be used.

In the case of water flow through pipes, a number of methods have been developed to determine the relationship between head loss and flow. The Hardy Cross method allows for any of these relationships to be used.

The general relationship between head loss and flow is:
:$h_f = k \cdot Q^$

where ''k'' is the head loss per unit flow and ''n'' is the flow exponent. In most design situations the values that make up ''k'', such as pipe length, diameter, and roughness, are taken to be known or assumed and thus the value of ''k'' can be determined for each pipe in the network. The values that make up ''k'' and the value of ''n'' change depending on the relation used to determine head loss. However, all relations are compatible with the Hardy Cross method.

It is also worth noting that the Hardy Cross method can be used to solve simple circuits and other flow like situations. In the case of simple circuits,
:$V = K \cdot I$
is equivalent to
:$h_f = k \cdot Q^$.
By setting the coefficient k to K, the flow rate Q to I and the exponent n to 1, the Hardy Cross method can be used to solve a simple circuit. However, because the relation between the voltage drop and current is linear, the Hardy Cross method is not necessary and the circuit can be solved using non-iterative methods.

Method of balancing heads

The method of balancing heads uses an initial guess that satisfies continuity of flow at each junction and then balances the flows until continuity of potential is also achieved over each loop in the system.

Proof (r denotes k)

The following proof is taken from Hardy Cross's paper, “Analysis of flow in networks of conduits or conductors.”, and can be verified by National Programme on Technology Enhanced Learning Water and Wastewater Engineering page, and Fundamentals of Hydraulic Engineering Systems by Robert J. Houghtalen.

If the initial guess of flow rates in each pipe is correct, the change in head over a loop in the system, $\Sigma r Q^$ would be equal to zero. However, if the initial guess is not correct, then the change in head will be non-zero and a change in flow, $\Delta Q$ must be applied. The new flow rate, $Q = Q_0 + \Delta Q$ is the sum of the old flow rate and some change in flow rate such that the change in head over the loop is zero. The sum of the change in head over the new loop will then be $\Sigma r (Q_0 + \Delta Q)^ = 0$.

The value of $\Sigma r (Q_0 + \Delta Q)^$ can be approximated using the Taylor expansion.

:$\Sigma r (Q_0 + \Delta Q)^ = \Sigma r (Q_0^n + n Q_0^ \Delta Q + ...) = 0$

For a small $\Delta Q$ compared to $Q_0$ the additional terms vanish, leaving:

:$\Sigma r (Q_0^n + n Q_0^ \Delta Q) = 0$

And solving for $\Delta Q$
:$\Sigma r Q_0^n = -\Sigma n r Q_0^ \Delta Q$

:$\Delta Q = -\frac$

The change in flow that will balance the head over the loop is approximated by $\Delta Q = -\frac$. However, this is only an approximation due to the terms that were ignored from the Taylor expansion. The change in head over the loop may not be zero, but it will be smaller than the initial guess. Multiple iterations of finding a new $\Delta Q$ will approximate to the correct solution.

Process

The method is as follows:
#Guess the flows in each pipe, making sure that the ''total in flow'' is equal to the ''total out flow'' at each junction. ''(The guess doesn't have to be good, but a good guess will reduce the time it takes to find the solution.)''
#Determine each closed loop in the system.
#For each loop, determine the clockwise head losses and counter-clockwise head losses. Head loss in each pipe is calculated using $h_f = r Q^$. Clockwise head losses are from flows in the clockwise direction and likewise for counter-clockwise.
#Determine the total head loss in the loop, $\Sigma r Q^$, by subtracting the counter-clockwise head loss from the clockwise head loss.
#For each loop, find $\Sigma n r Q^$ without reference to direction (all values should be positive).
#The change in flow is equal to $\frac$.
#If the change in flow is positive, apply it to all pipes of the loop in the counter-clockwise direction. If the change in flow is negative, apply it to all pipes of the loop in the clockwise direction.
#Continue from step 3 until the change in flow is within a satisfactory range.

Method of balancing flows (section incomplete)

The method of balancing flows uses an initial guess that satisfies continuity of potential over each loop and then balances the flows until continuity of flow is also achieved at each junction.

Advantages of the Hardy Cross method

Simple mathematics

The Hardy Cross method is useful because it relies on only simple mathematics, circumventing the need to solve a system of equations. Without the Hardy Cross methods, engineers would have to solve complex systems of equations with variable exponents that cannot easily be solved by hand.

Self correcting

The Hardy Cross method iteratively corrects for the mistakes in the initial guess used to solve the problem. Subsequent mistakes in calculation are also iteratively corrected. If the method is followed correctly, the proper flow in each pipe can still be found if small mathematical errors are consistently made in the process. As long as the last few iterations are done with attention to detail, the solution will still be correct. In fact, it is possible to intentionally leave off decimals in the early iterations of the method to run the calculations faster.

Example

The Hardy Cross method can be used to calculate the flow distribution in a pipe network. Consider the example of a simple pipe flow network shown at the right. For this example, the in and out flows will be 10 liters per second. We will consider n to be 2, and the head loss per unit flow ''r'', and initial flow guess for each pipe as follows:

We solve the network by method of balancing heads, following the steps outlined in method process above.

1. The initial guesses are set up so that continuity of flow is maintained at each junction in the network.

2. The loops of the system are identified as loop 1-2-3 and loop 2-3-4.

3. The head losses in each pipe are determined.

For loop 1-2-3, the sum of the clockwise head losses is 25 and the sum of the counter-clockwise head losses is 125.

For loop 2-3-4, the sum of the clockwise head losses is 125 and the sum of the counter-clockwise head losses is 25.

4. The total clockwise head loss in loop 1-2-3 is $25-125 = -100$. The total clockwise head loss in loop 2-3-4 is $125-25 = 100$.

5. The value of $\Sigma n r Q^$ is determined for each loop. It is found to be 60 in both loops (due to symmetry), as shown in the figure.

6. The change in flow is found for each loop using the equation $\frac$. For loop 1-2-3, the change in flow is equal to $-100/60 = -1.66$ and for loop 2-3-4 the change in flow is equal to $100/60 = 1.66$.

7. The change in flow is applied across the loops. For loop 1-2-3, the change in flow is negative so its absolute value is applied in the clockwise direction. For loop 2-3-4, the change in flow is positive so its absolute value is applied in the counter-clockwise direction. For pipe 2-3, which is in both loops, the changes in flow are cumulative.

The process then repeats from step 3 until the change in flow becomes sufficiently small or goes to zero.

3. The total head loss in Loop 1-2-3 is

Notice that the clockwise head loss is equal to the counter-clockwise head loss. This means that the flow in this loop is balanced and the flow rates are correct. The total head loss in loop 2-3-4 will also be balanced (again due to symmetry).

In this case, the method found the correct solution in one iteration. For other networks, it may take multiple iterations until the flows in the pipes are correct or approximately correct.

See also

* Pipe network analysis
* Moment distribution method

References

{{reflist

Hydraulic engineering