The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling

tessellation A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety ...

(or

honeycomb A honeycomb is a mass of Triangular prismatic honeycomb#Hexagonal prismatic honeycomb, hexagonal prismatic cells built from beeswax by honey bees in their beehive, nests to contain their brood (eggs, larvae, and pupae) and stores of honey and pol ...

) in

Euclidean 3-space In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values (''coordinates'') are required to determine the position of a point. Most commonly, it is the three-dim ...

. It is composed of alternating regular

octahedra In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...

and

tetrahedra In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...

in a ratio of 1:2. Other names include half cubic honeycomb, half cubic cellulation, or tetragonal disphenoidal cellulation.

John Horton Conway John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician. He was active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many b ...

calls this honeycomb a tetroctahedrille, and its dual a

dodecahedrille The rhombic dodecahedral honeycomb (also dodecahedrille) is a space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space. It is the Voronoi diagram of the face-centered cubic sphere-packing, which has the densest possi ...

. R. Buckminster Fuller combines the two words octahedron and tetrahedron into octet truss, a rhombohedron consisting of one octahedron (or two square pyramids) and two opposite tetrahedra. It is

vertex-transitive In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face i ...

with 8

and 6

around each vertex. It is

edge-transitive In geometry, a polytope (for example, a polygon or a polyhedron) or a Tessellation, tiling is isotoxal () or edge-transitive if its Symmetry, symmetries act Transitive group action, transitively on its Edge (geometry), edges. Informally, this mea ...

with 2 tetrahedra and 2 octahedra alternating on each edge. It is part of an infinite family of uniform honeycombs called alternated hypercubic honeycombs, formed as an alternation of a hypercubic honeycomb and being composed of

demihypercube In geometry, demihypercubes (also called ''n-demicubes'', ''n-hemicubes'', and ''half measure polytopes'') are a class of ''n''-polytopes constructed from alternation of an ''n''-hypercube, labeled as ''hγn'' for being ''half'' of the hype ...

and

cross-polytope In geometry, a cross-polytope, hyperoctahedron, orthoplex, staurotope, or cocube is a regular, convex polytope that exists in ''n''- dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a reg ...

facets. It is also part of another infinite family of uniform honeycombs called

simplectic honeycomb In geometry, the simplicial honeycomb (or -simplex honeycomb) is a dimensional infinite series of honeycombs, based on the _n affine Coxeter group symmetry. It is represented by a Coxeter-Dynkin diagram as a cyclic graph of nodes with one node ...

s. In this case of 3-space, the

cubic honeycomb The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space made up of cube, cubic cells. It has 4 cubes around every edge, and 8 cubes around each verte ...

is alternated, reducing the cubic cells to tetrahedra, and the deleted vertices create octahedral voids. As such it can be represented by an extended

Schläfli symbol In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations. The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...

h as containing ''half'' the vertices of the cubic honeycomb. There is a similar honeycomb called

gyrated tetrahedral-octahedral honeycomb The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2. Other names incl ...

which has layers rotated 60 degrees so half the edges have neighboring rather than alternating tetrahedra and octahedra. The tetrahedral-octahedral honeycomb can have its symmetry doubled by placing tetrahedra on the octahedral cells, creating a nonuniform honeycomb consisting of

and

(as triangular antiprisms). Its vertex figure is an order-3 truncated triakis tetrahedron. This honeycomb is the dual of the

triakis truncated tetrahedral honeycomb The triakis truncated tetrahedral honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of triakis truncated tetrahedra. It was discovered in 1914. Voronoi tessellation It is the Voronoi tessellation of the ca ...

, with triakis truncated tetrahedral cells.

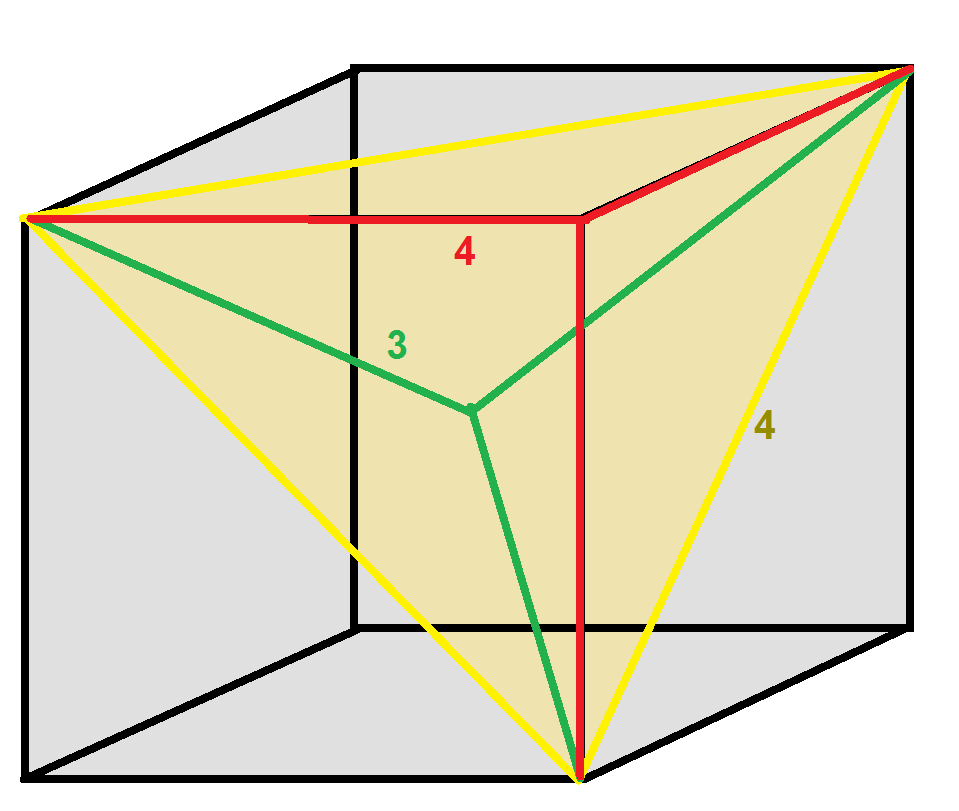
Cartesian coordinates

For an ''alternated cubic honeycomb'', with edges parallel to the axes and with an edge length of 1, the

Cartesian coordinates In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...

of the vertices are: (For all integral values: ''i'',''j'',''k'' with ''i''+''j''+''k''

even Even may refer to: General * Even (given name), a Norwegian male personal name * Even (surname), a Breton surname * Even (people), an ethnic group from Siberia and Russian Far East **Even language, a language spoken by the Evens * Odd and Even, a ...

) :(i, j, k)

Symmetry

There are two reflective constructions and many alternated

ones; examples:

Alternated cubic honeycomb slices

The ''alternated cubic honeycomb'' can be sliced into sections, where new square faces are created from inside of the octahedron. Each slice will contain up and downward facing

square pyramid In geometry, a square pyramid is a Pyramid (geometry), pyramid with a square base and four triangles, having a total of five faces. If the Apex (geometry), apex of the pyramid is directly above the center of the square, it is a ''right square p ...

s and

sitting on their edges. A second slice direction needs no new faces and includes alternating tetrahedral and octahedral. This slab honeycomb is a scaliform honeycomb rather than uniform because it has nonuniform cells.

Projection by folding

The ''alternated cubic honeycomb'' can be orthogonally projected into the planar

square tiling In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane consisting of four squares around every vertex. John Horton Conway called it a quadrille. Structure and properties The square tili ...

by a geometric folding operation that maps one pairs of mirrors into each other. The projection of the ''alternated cubic honeycomb'' creates two offset copies of the square tiling

vertex arrangement In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes. For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equa ...

of the plane:

A3/D3 lattice

Its

represents an A₃ lattice or ''D₃ lattice''. This lattice is known as the

face-centered cubic lattice In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of ...

in crystallography and is also referred to as the cubic close packed lattice as its vertices are the centers of a close-packing with equal spheres that achieves the highest possible average density. The tetrahedral-octahedral honeycomb is the 3-dimensional case of a

. Its Voronoi cell is a

rhombic dodecahedron In geometry, the rhombic dodecahedron is a Polyhedron#Convex_polyhedra, convex polyhedron with 12 congruence (geometry), congruent rhombus, rhombic face (geometry), faces. It has 24 edge (geometry), edges, and 14 vertex (geometry), vertices of 2 ...

, the dual of the

cuboctahedron A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...

vertex figure for the tet-oct honeycomb. The D packing can be constructed by the union of two D₃ (or A₃) lattices. The D packing is only a lattice for even dimensions. The kissing number is 2²=4, (2ⁿ⁻¹ for n<8, 240 for n=8, and 2n(n−1) for n>8). : ∪ The A or D lattice (also called A or D) can be constructed by the union of all four A₃ lattices, and is identical to the

of the disphenoid tetrahedral honeycomb, dual honeycomb of the uniform

bitruncated cubic honeycomb The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space made up of truncated octahedron, truncated octahedra (or, equivalently, Bitruncation (geometry), bitruncated cubes). It has 4 ...

: It is also the

body centered cubic In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of ...

, the union of two

s in dual positions. : ∪ ∪ ∪ = dual of = ∪ . The

kissing number In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing (arrangement o ...

of the D lattice is 8 and its Voronoi tessellation is a

, , containing all truncated octahedral

Voronoi cell In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. It can be classified also as a tessellation. In the simplest case, these objects are just finitely many points in the plane (calle ...

s, .

Related honeycombs

C3 honeycombs

The ,3,4 ,

Coxeter group In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean ref ...

generates 15 permutations of uniform honeycombs, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.

B3 honeycombs

The ,3^1,1 ,

generates 9 permutations of uniform honeycombs, 4 with distinct geometry including the alternated cubic honeycomb.

A3 honeycombs

This honeycomb is one of five distinct uniform honeycombs
6-1 cases, skipping one with zero marks constructed by the

_3

. The symmetry can be multiplied by the symmetry of rings in the

Coxeter–Dynkin diagram In geometry, a Harold Scott MacDonald Coxeter, Coxeter–Eugene Dynkin, Dynkin diagram (or Coxeter diagram, Coxeter graph) is a Graph (discrete mathematics), graph with numerically labeled edges (called branches) representing a Coxeter group or ...

Quasiregular honeycombs

Cantic cubic honeycomb

The cantic cubic honeycomb, cantic cubic cellulation or truncated half cubic honeycomb is a uniform space-filling

(or

) in Euclidean 3-space. It is composed of

truncated octahedra In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 ...

, cuboctahedra and

truncated tetrahedra In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncating all 4 vertices of a regular tetrahedron. ...

in a ratio of 1:1:2. Its

vertex figure In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off. Definitions Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...

is a rectangular

pyramid A pyramid () is a structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a pyramid in the geometric sense. The base of a pyramid can be of any polygon shape, such as trian ...

calls this honeycomb a truncated tetraoctahedrille, and its dual half oblate octahedrille. : Truncated alternated cubic tiling

Symmetry

It has two different uniform constructions. The

_3

construction can be seen with alternately colored

Related honeycombs

It is related to the cantellated cubic honeycomb. Rhombicuboctahedra are reduced to truncated octahedra, and cubes are reduced to truncated tetrahedra.

Runcic cubic honeycomb

The runcic cubic honeycomb or runcic cubic cellulation is a uniform space-filling

(or

) in Euclidean 3-space. It is composed of rhombicuboctahedra,

cube A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...

s, and

in a ratio of 1:1:2. Its

is a triangular frustum, with a tetrahedron on one end, cube on the opposite end, and three rhombicuboctahedra around the trapezoidal sides.

calls this honeycomb a 3-RCO-trille, and its dual quarter cubille. : HC A5-P2-P1

Quarter cubille

The dual of a ''runcic cubic honeycomb'' is called a quarter cubille, with

Coxeter diagram Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century. Coxeter was born in England and educated ...

, with faces in 2 of 4 hyperplanes of the

_4

, ,3^1,1symmetry fundamental domain. Cells can be seen as 1/4 of dissected cube, using 4 vertices and the center. Four cells exist around 6 edges, and 3 cells around 3 edges. : Quarter cubille cell

Related honeycombs

It is related to the

runcinated cubic honeycomb The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a re ...

, with quarter of the cubes alternated into tetrahedra, and half expanded into rhombicuboctahedra. This honeycomb can be divided on

truncated square tiling In geometry, the truncated square tiling is a semiregular tiling, semiregular tiling by regular polygons of the Euclidean plane with one square (geometry), square and two octagons on each vertex (geometry), vertex. This is the only edge-to-edge t ...

planes, using the octagons centers of the rhombicuboctahedra, creating

square cupola In geometry, the square cupola (sometimes called lesser dome) is a cupola with an octagonal In geometry, an octagon () is an eight-sided polygon or 8-gon. A '' regular octagon'' has Schläfli symbol and can also be constructed as a quasireg ...

e. This scaliform honeycomb is represented by Coxeter diagram , and symbol s₃, with

coxeter notation In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, ...

symmetry ⁺,4,4 : Runcic_snub_244_honeycomb

Runcicantic cubic honeycomb

The runcicantic cubic honeycomb or runcicantic cubic cellulation is a uniform space-filling

(or

) in Euclidean 3-space. It is composed of truncated cuboctahedra,

truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces (6 octagonal and 8 triangle (geometry), triangular), 36 edges, and 24 vertices. If the truncated cube has unit edge length, its dual triak ...

s and

in a ratio of 1:1:2, with a mirrored sphenoid

. It is related to the runcicantellated cubic honeycomb.

calls this honeycomb a f-tCO-trille, and its dual half pyramidille. : HC A6-A2-A1

Half pyramidille

The dual to the ''runcitruncated cubic honeycomb'' is called a half pyramidille, with

. Faces exist in 3 of 4 hyperplanes of the ,3^1,1

_3

Coxeter group. Cells are irregular pyramids and can be seen as 1/12 of a

, or 1/24 of a

, each defined with three corner and the cube center. : Half pyramidille cell

Related skew apeirohedra

A related uniform skew apeirohedron exists with the same

, but triangles and square removed. It can be seen as truncated tetrahedra and truncated cubes augmented together. : Runcicantic_cubic_honeycomb_apeirohedron_6688

Runcicantic_cubic_honeycomb_apeirohedron_6688

Related honeycombs

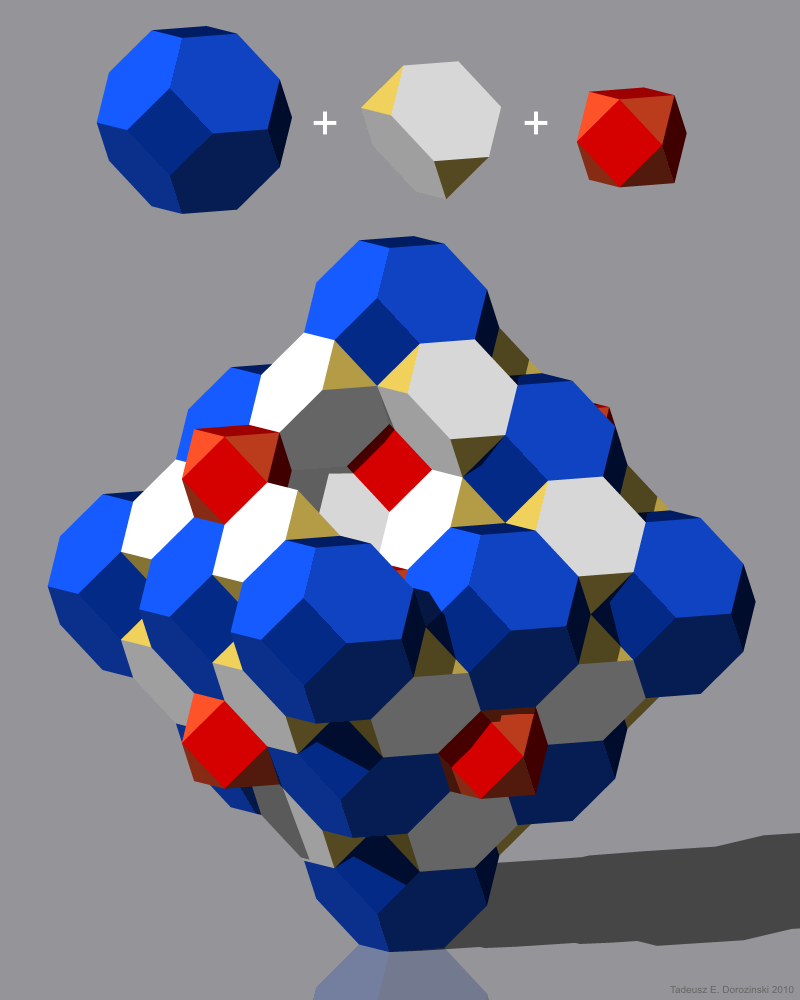
Gyrated tetrahedral-octahedral honeycomb

The gyrated tetrahedral-octahedral honeycomb or gyrated alternated cubic honeycomb is a space-filling

(or

) in

made up of

and

in a ratio of 1:2. It is vertex-uniform with 8 tetrahedra and 6 octahedra around each vertex. It is not edge-uniform. All edges have 2 tetrahedra and 2 octahedra, but some are alternating, and some are paired. : Gyrated alternated cubic honeycomb

It can be seen as reflective layers of this layer honeycomb:

Construction by gyration

This is a less symmetric version of another honeycomb, tetrahedral-octahedral honeycomb, in which each edge is surrounded by alternating tetrahedra and octahedra. Both can be considered as consisting of layers one cell thick, within which the two kinds of cell strictly alternate. Because the faces on the planes separating these layers form a regular pattern of triangles, adjacent layers can be placed so that each octahedron in one layer meets a tetrahedron in the next layer, or so that each cell meets a cell of its own kind (the layer boundary thus becomes a

reflection Reflection or reflexion may refer to: Science and technology * Reflection (physics), a common wave phenomenon ** Specular reflection, mirror-like reflection of waves from a surface *** Mirror image, a reflection in a mirror or in water ** Diffuse r ...

plane). The latter form is called ''gyrated''. The vertex figure is called a

triangular orthobicupola In geometry, the triangular orthobicupola is one of the Johnson solids (). As the name suggests, it can be constructed by attaching two triangular cupolas () along their bases. It has an equal number of squares and triangles at each vertex; howe ...

, compared to the tetrahedral-octahedral honeycomb whose vertex figure

in a lower symmetry is called a ''triangular gyrobicupola'', so the gyro- prefix is reversed in usage.

Construction by alternation

The geometry can also be constructed with an alternation operation applied to a

hexagonal prismatic honeycomb The triangular prismatic honeycomb or triangular prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed entirely of triangular prisms. It is constructed from a triangular tiling extruded into pr ...

. The

hexagonal prism In geometry, the hexagonal prism is a Prism (geometry), prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 face (geometry), faces, 18 Edge (geometry), edges, and 12 vertex (geometry), vertices.. As a semiregular polyhedro ...

cells become

and the voids create

triangular bipyramid A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of a t ...

s which can be divided into pairs of

of this honeycomb. This honeycomb with bipyramids is called a ditetrahedral-octahedral honeycomb. There are 3 Coxeter-Dynkin diagrams, which can be seen as 1, 2, or 3 colors of octahedra: # # #

Gyroelongated alternated cubic honeycomb

The gyroelongated alternated cubic honeycomb or elongated triangular antiprismatic cellulation is a space-filling

(or

) in

. It is composed of

triangular prism In geometry, a triangular prism or trigonal prism is a Prism (geometry), prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a ''right triangular prism''. A right triangul ...

s, and

in a ratio of 1:2:2. It is vertex-transitive with 3 octahedra, 4 tetrahedra, 6 triangular prisms around each vertex. It is one of 28

convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform polytope, uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex polyhedron, convex uniform polyhedron, uniform polyhedral cells. Twenty-eight such honey ...

s. The elongated alternated cubic honeycomb has the same arrangement of cells at each vertex, but the overall arrangement differs. In the ''elongated'' form, each prism meets a tetrahedron at one of its triangular faces and an octahedron at the other; in the ''gyroelongated'' form, the prism meets the same kind of

deltahedron A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron was named by Martyn Cundy, after the Greek capital letter delta resembling a triangular shape Δ. Deltahedra can be categorized by the property of convexi ...

at each end. :

Elongated alternated cubic honeycomb

The elongated alternated cubic honeycomb or elongated triangular gyroprismatic cellulation is a space-filling

(or

) in

. It is composed of

s, and

in a ratio of 1:2:2. It is vertex-transitive with 3 octahedra, 4 tetrahedra, 6 triangular prisms around each vertex. Each prism meets an octahedron at one end and a tetrahedron at the other. It is one of 28

s. It has a ''gyrated'' form called the gyroelongated alternated cubic honeycomb with the same arrangement of cells at each vertex. :

Notes

References

* John H. Conway, Heidi Burgiel,

Chaim Goodman-Strauss Chaim Goodman-Strauss (born June 22, 1967 in Austin, Texas) is an American mathematician who works in convex geometry, especially aperiodic tiling. He retired from the faculty of the University of Arkansas and currently serves as outreach mathem ...

, (2008) ''The Symmetries of Things'', (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292–298, includes all the nonprismatic forms) * George Olshevsky, ''Uniform Panoploid Tetracombs'', Manuscript (2006) ''(Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)'' *

Branko Grünbaum Branko Grünbaum (; 2 October 1929 – 14 September 2018) was a Croatian-born mathematician of Jewish descentGeombinatorics Alexander Soifer is a Russian-born American mathematician and mathematics author. Soifer obtained his Ph.D. in 1973 and has been a professor of mathematics at the University of Colorado since 1979. He was visiting fellow at Princeton University ...

4(1994), 49 - 56. * Norman Johnson ''Uniform Polytopes'', Manuscript (1991) * * * Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,

** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380–407, MR 2,10(1.9 Uniform space-fillings) ** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3-45* A. Andreini, ''Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative'' (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129. * D. M. Y. Sommerville, ''An Introduction to the Geometry of n Dimensions.'' New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes *

External links

Architectural design made with Tetrahedrons and regular Pyramids based square.(2003)
*

{{Honeycombs 3-honeycombs Uniform 4-polytopes

Cartesian coordinates

Symmetry

Alternated cubic honeycomb slices

Projection by folding

A3/D3 lattice

Related honeycombs

C3 honeycombs

B3 honeycombs

A3 honeycombs

Quasiregular honeycombs

Cantic cubic honeycomb

Symmetry

Related honeycombs

Runcic cubic honeycomb

Quarter cubille

Related honeycombs

Runcicantic cubic honeycomb

Half pyramidille

Related skew apeirohedra

Related honeycombs

Gyrated tetrahedral-octahedral honeycomb

Construction by gyration

Construction by alternation

Gyroelongated alternated cubic honeycomb

Elongated alternated cubic honeycomb

See also

Notes

References

External links