grand antiprism

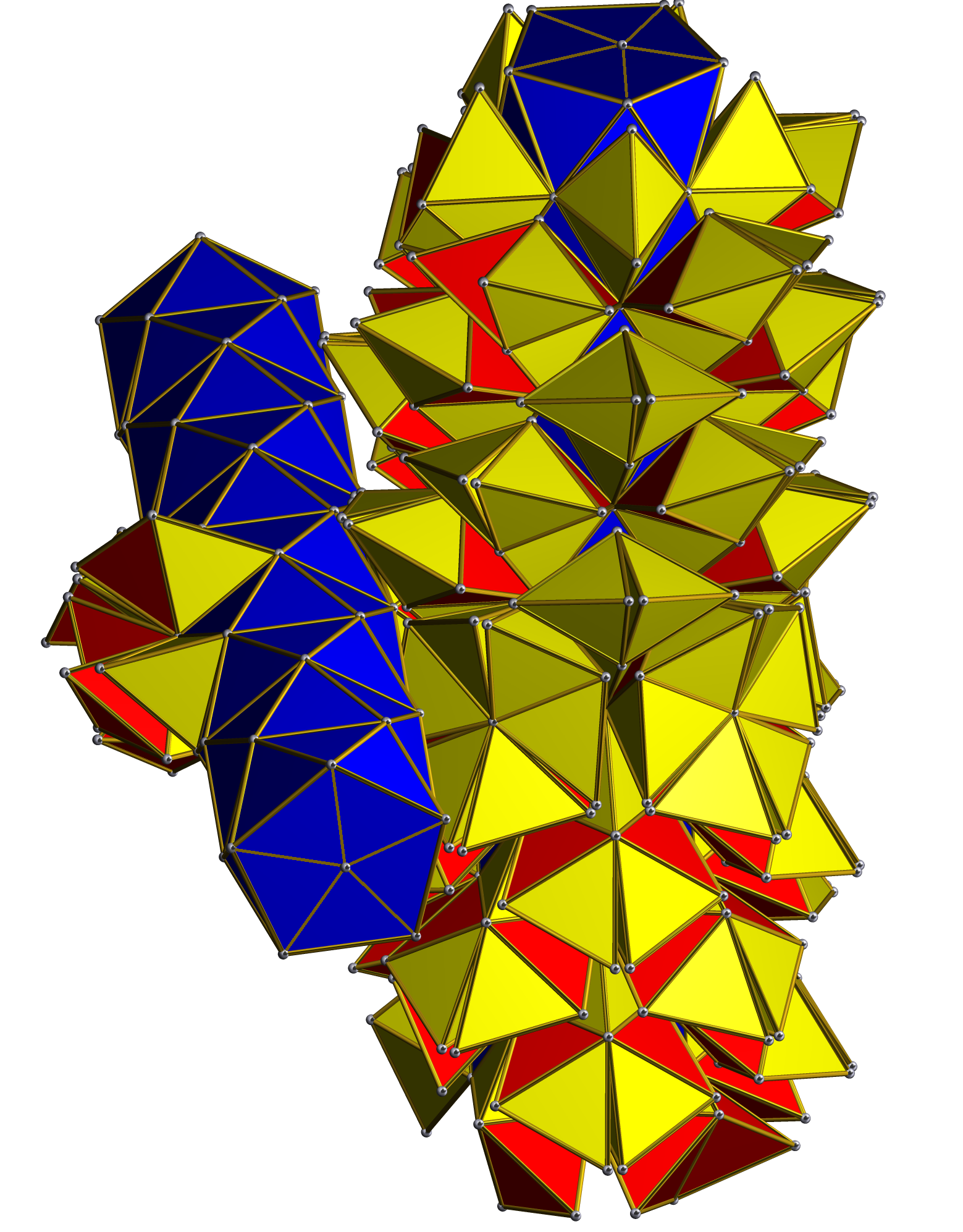In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polytope, discovered in 1965 by John H. Conway and Michael Guy. Topologically, under its highest symmetry, the pentagonal antiprisms have ''D_5d'' symmetry and there are two types of tetrahedra, one with ''S₄'' symmetry and one with ''C_s'' symmetry.

Alternate names

* Pentagonal double antiprismoid Norman W. Johnson
* Gap (Jonathan Bowers: for grand antiprism)

Structure

20 stacked pentagonal antiprisms occur in two disjoint rings of 10 antiprisms each. The antiprisms in each ring are joined to each other via their pentagonal faces. The two rings are mutually perpendicular, in a structure similar to a duoprism.

The 300 tetrahedra join the two rings to each other, and are laid out in a 2-dimensional arrangement topologically equivalent to the 2-torus and the ridge of the duocylinder. These can be further divided into three sets. 100 face mate to one ring, 100 face mate to the other ring, and 100 are centered at the exact midpoint of the duocylinder and edge mate to both rings. This latter set forms a flat torus and can be "unrolled" into a flat 10×10 square array of tetrahedra that meet only at their edges and vertices. See figure below.

In addition the 300 tetrahedra can be partitioned into 10 disjoint Boerdijk–Coxeter helices of 30 cells each that close back on each other. The two pentagonal antiprism tubes, plus the 10 BC helices, form an irregular discrete Hopf fibration of the grand antiprism that Hopf maps to the faces of a pentagonal antiprism. The two tubes map to the two pentagonal faces and the 10 BC helices map to the 10 triangular faces.

The structure of the grand antiprism is analogous to that of the 3-dimensional antiprisms. However, the grand antiprism is the only convex uniform analogue of the antiprism in 4 dimensions (although the 16-cell may be regarded as a regular analogue of the ''digonal antiprism''). The only nonconvex uniform 4-dimensional antiprism analogue uses pentagrammic crossed-antiprisms instead of pentagonal antiprisms, and is called the '' pentagrammic double antiprismoid''.

Vertex figure

The vertex figure of the grand antiprism is a sphenocorona or ''dissected regular icosahedron'': a regular icosahedron with two adjacent vertices removed. In their place 8 triangles are replaced by a pair of trapezoids, edge lengths φ, 1, 1, 1 (where φ is the golden ratio), joined together along their edge of length φ, to give a tetradecahedron whose faces are the 2 trapezoids and the 12 remaining equilateral triangles.

Construction

The grand antiprism can be constructed by ''diminishing'' the 600-cell: subtracting 20 pyramids whose bases are three-dimensional pentagonal antiprisms. Conversely, the two rings of pentagonal antiprisms in the grand antiprism may be triangulated by 10 tetrahedra joined to the triangular faces of each antiprism, and a circle of 5 tetrahedra between every pair of antiprisms, joining the 10 tetrahedra of each, yielding 150 tetrahedra per ring. These combined with the 300 tetrahedra that join the two rings together yield the 600 tetrahedra of the 600-cell.

This diminishing may be realized by removing two rings of 10 vertices from the 600-cell, each lying in mutually orthogonal planes. Each ring of removed vertices creates a stack of pentagonal antiprisms on the convex hull. This relationship is analogous to how a pentagonal antiprism can be constructed from an icosahedron by removing two opposite vertices, thereby removing 5 triangles from the opposite 'poles' of the icosahedron, leaving the 10 equatorial triangles and two pentagons on the top and bottom.

(The snub 24-cell can also be constructed by another diminishing of the 600-cell, removing 24 icosahedral pyramids. Equivalently, this may be realized as taking the convex hull of the vertices remaining after 24 vertices, corresponding to those of an inscribed 24-cell, are removed from the 600-cell.)

Alternatively, it can also be constructed from the decagonal ditetragoltriate (the convex hull of two perpendicular nonuniform 10-10 duoprisms where the ratio of the two decagons are in the golden ratio) via an alternation process. The decagonal prisms alternate into pentagonal antiprisms, the rectangular trapezoprisms alternate into tetrahedra with two new regular tetrahedra (representing a non-corealmic triangular bipyramid) created at the deleted vertices. This is the only uniform solution for the p-gonal double antiprismoids alongside its conjugate, the pentagrammic double antiprismoid from the decagrammic ditetragoltriate.

Projections

These are two perspective projections, projecting the polytope into a hypersphere, and applying a stereographic projection into 3-space.

See also

* 600-cell
* Snub 24-cell
* Uniform 4-polytope
* Duoprism
* Duocylinder

Notes

References

*
Kaleidoscopes: Selected Writings of H.S.M. Coxeter
', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,
** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559-5912.8 The Grand Antiprism
*
*
* John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'' 2008, (Chapter 26) The Grand Antiprism

Grand Antiprism and Quaternions
Mehmet Koca, Mudhahir Al-Ajmi, Nazife Ozdes Koca (2009); Mehmet Koca et al. 2009 J. Phys. A: Math. Theor. 42 495201

External links

In the Belly of the Grand Antiprism
(middle section, describing the analogy with the icosahedron and the pentagonal antiprism)

{{Polytopes

Uniform 4-polytopes