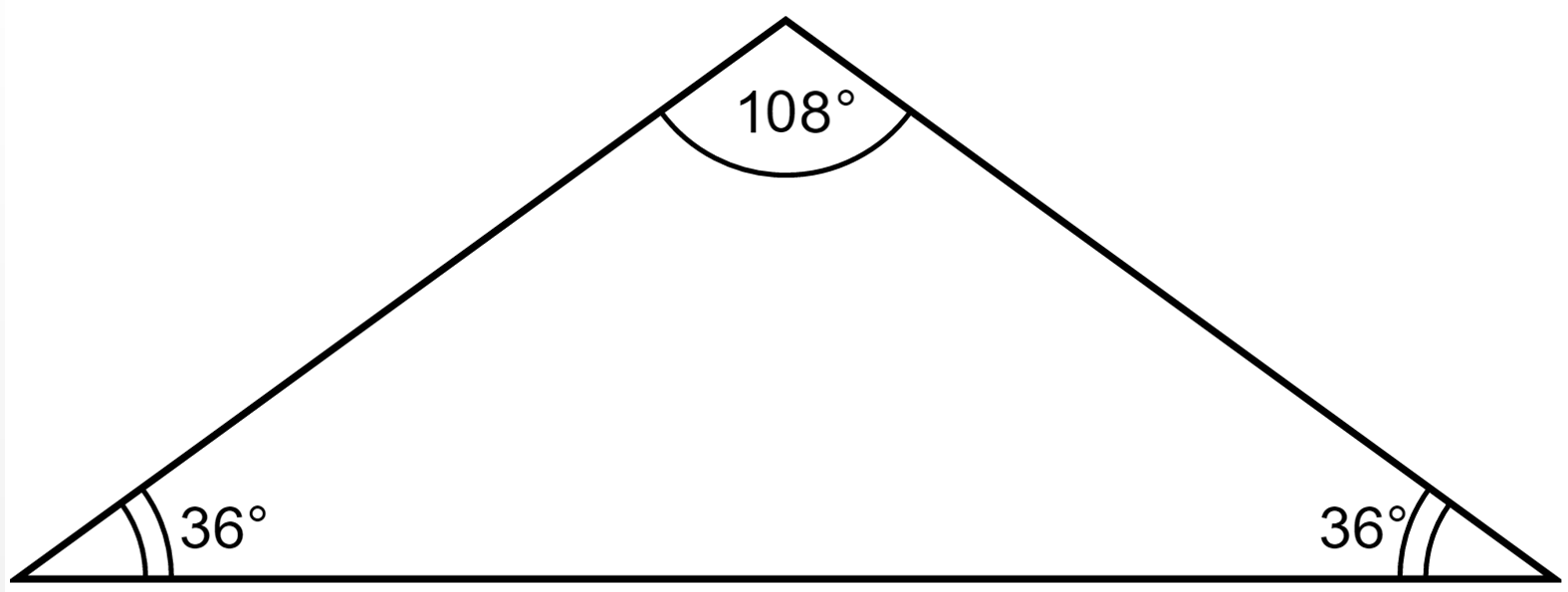A golden triangle, also called a sublime triangle, is an

isosceles In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter versio ...

triangle A triangle is a polygon with three Edge (geometry), edges and three Vertex (geometry), vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, an ...

in which the duplicated side is in the

golden ratio In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( ...

\varphi

to the base side: :

= \varphi =  \approx 1.618~034~.

Angles

* The vertex

angle In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. Angles formed by two ...

is: ::

\theta = 2\arcsin = 2\arcsin = 2\arcsin = ~\text = 36^\circ.

:Hence the golden triangle is an

acute Acute may refer to: Science and technology * Acute angle ** Acute triangle ** Acute, a leaf shape in the glossary of leaf morphology * Acute (medicine), a disease that it is of short duration and of recent onset. ** Acute toxicity, the adverse eff ...

(isosceles) triangle. * Since the angles of a triangle sum to

\pi

radians, each of the base angles (CBX and CXB) is: ::

\beta = ~\text = ~\text = 72^\circ.

:Note: ::

\beta = \arccos\left(\frac\right)\,\text = ~\text = 72^\circ.

* The golden triangle is uniquely identified as the only triangle to have its three angles in the ratio 1 : 2 : 2 (36°, 72°, 72°).

In other geometric figures

* Golden triangles can be found in the spikes of regular

pentagram A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle aroun ...

s. * Golden triangles can also be found in a regular

decagon In geometry, a decagon (from the Greek δέκα ''déka'' and γωνία ''gonía,'' "ten angles") is a ten-sided polygon or 10-gon.. The total sum of the interior angles of a simple decagon is 1440°. A self-intersecting ''regular decagon'' i ...

, an equiangular and equilateral ten-sided

polygon In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed ''polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two toge ...

, by connecting any two adjacent vertices to the center. This is because: 180(10−2)/10 = 144° is the interior angle, and bisecting it through the vertex to the center: 144/2 = 72°. * Also, golden triangles are found in the nets of several stellations of

dodecahedron In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagon ...

s and

icosahedron In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrica ...

Logarithmic spiral

The golden triangle is used to form some points of a

logarithmic spiral A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral curve that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer (1525) who called it an "eternal line" ("ewige Linie"). Mor ...

. By bisecting one of the base angles, a new point is created that in turn, makes another golden triangle. The bisection process can be continued indefinitely, creating an infinite number of golden triangles. A logarithmic spiral can be drawn through the vertices. This spiral is also known as an equiangular spiral, a term coined by

René Descartes René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathem ...

. "If a straight line is drawn from the pole to any point on the curve, it cuts the curve at precisely the same angle," hence ''equiangular''.

Golden gnomon

Closely related to the golden triangle is the golden

gnomon A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields. History A painted stick dating from 2300 BC that was excavated at the astronomical site of Taosi is the ol ...

, which is the isosceles triangle in which the ratio of the equal side lengths to the base length is the

reciprocal Reciprocal may refer to: In mathematics * Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal'' * Reciprocal polynomial, a polynomial obtained from another pol ...

\tfrac

of the

\varphi

. "The golden triangle has a ratio of base length to side length equal to the golden section φ, whereas the golden gnomon has the ratio of side length to base length equal to the golden section φ." :

=  =  \approx 0.618034.

Angles

(The distances AX and CX are both ''a''′ = ''a'' = φ , and the distance AC is ''b''′ = φ², as seen in the figure.) * The apex angle AXC is: ::

\theta' = 2\arcsin = 2\arcsin = 2\arcsin = ~\text = 108^\circ.

:Hence the golden gnomon is an obtuse (isosceles) triangle. :

(

Note:

\theta' = \arccos\left(\frac\right)\,\text = ~\text = 108^.)

* Since the angles of the triangle AXC sum to

\pi

radians, each of the base angles CAX and ACX is: ::

\beta' = \theta = ~\text = ~\text = 36^.

:Note:

\beta' = \theta = \arccos\left(\frac\right)\,\text = ~\text = 36^.

* The golden gnomon is uniquely identified as a triangle having its three angles in the ratio 1 : 1 : 3 (36°, 36°, 108°). Its base angles are 36° each, which is the same as the apex of the golden triangle.

Bisections

* By cutting one of its base angles into 2 equal angles, a golden triangle can be bisected into a golden triangle and a golden gnomon. * By cutting its apex angle into 2 angles, one being twice the other, a golden gnomon can be bisected into a golden triangle and a golden gnomon. * A golden gnomon and a golden triangle with their equal sides matching each other in length, are also referred to as the obtuse and acute Robinson triangles.

Tilings

* A golden triangle and two golden gnomons tile a regular

pentagon In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°. A pentagon may be simpl ...

. * These isosceles triangles can be used to produce

Penrose tiling A Penrose tiling is an example of an aperiodic tiling. Here, a ''tiling'' is a covering of the plane by non-overlapping polygons or other shapes, and ''aperiodic'' means that shifting any tiling with these shapes by any finite distance, without ...

s. Penrose tiles are made from kites and darts. A kite is made from two golden triangles, and a dart is made from two gnomons.

References

External links

* *
Robinson triangles
at Tilings Encyclopedia
Golden triangle according to Euclid

at Tartapelago by Giorgio Pietrocola {{DEFAULTSORT:Golden Triangle (Mathematics) Types of triangles Golden ratio

Angles

In other geometric figures

Logarithmic spiral

Golden gnomon

Angles

Bisections

Tilings

See also

References

External links