Glauber Dynamics on:
[Wikipedia]
[Google]
[Amazon]
In
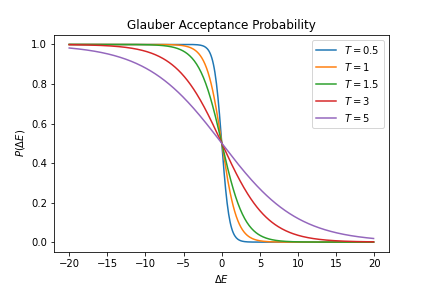 The Glauber algorithm can be compared to the
The Glauber algorithm can be compared to the 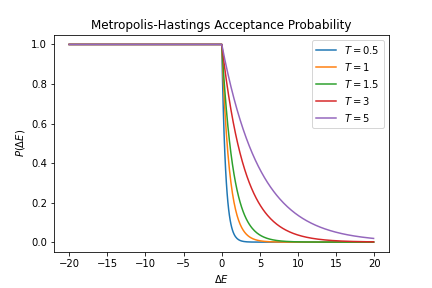 Although both of the acceptance probabilities approximate a step curve and they are almost indistinguishable at very low temperatures, they differ when temperature gets high. For an Ising model on a 2d lattice, the critical temperature is .
At thermal equilibrium, the Glauber and Metropolis algorithms should give identical results. In general, at equilibrium, any MCMC algorithm should produce the same distribution, as long as the algorithm satisfies
Although both of the acceptance probabilities approximate a step curve and they are almost indistinguishable at very low temperatures, they differ when temperature gets high. For an Ising model on a 2d lattice, the critical temperature is .
At thermal equilibrium, the Glauber and Metropolis algorithms should give identical results. In general, at equilibrium, any MCMC algorithm should produce the same distribution, as long as the algorithm satisfies
CRAN
statistical physics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applicati ...
, Glauber dynamics is a way to simulate
A simulation is an imitative representation of a process or system that could exist in the real world. In this broad sense, simulation can often be used interchangeably with model. Sometimes a clear distinction between the two terms is made, in ...
the Ising model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that r ...
(a model of magnetism
Magnetism is the class of physical attributes that occur through a magnetic field, which allows objects to attract or repel each other. Because both electric currents and magnetic moments of elementary particles give rise to a magnetic field, ...
) on a computer.
The algorithm is named after Roy J. Glauber
Roy Jay Glauber (September 1, 1925 – December 26, 2018) was an American theoretical physicist. He was the Mallinckrodt Professor of Physics at Harvard University and Adjunct Professor of Optical Sciences at the University of Arizona. Born in N ...
.
The algorithm
TheIsing model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that r ...
is an abstract model for the magnetic
Magnetism is the class of physical attributes that occur through a magnetic field, which allows objects to attract or repel each other. Because both electric currents and magnetic moments of elementary particles give rise to a magnetic field, m ...
interaction of neighboring atom
Atoms are the basic particles of the chemical elements. An atom consists of a atomic nucleus, nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished fr ...
s. It is conventionally considered on a two-dimensional square lattice, with magnetic interactions occurring only between nearest neighbors. In this model, each lattice site is given a spin
Spin or spinning most often refers to:
* Spin (physics) or particle spin, a fundamental property of elementary particles
* Spin quantum number, a number which defines the value of a particle's spin
* Spinning (textiles), the creation of yarn or thr ...
that is either up (+1) or down (-1); the x and y are the grid coordinates. Glauber's algorithm becomes:
# Choose a location at random.
# Sum the spins of the nearest-neighbors. For a two-D square lattice, there are four: .
# Compute the change in energy if the spin at x, y were to flip. This is given by the Hamiltonian for the Ising model; it is
# Flip the spin with probability given by the Fermi function
Enrico Fermi (; 29 September 1901 – 28 November 1954) was an Italian and naturalized American physicist, renowned for being the creator of the world's first artificial nuclear reactor, the Chicago Pile-1, and a member of the Manhattan Project ...
where T is the temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
.
# Go To Step 1.
In Glauber algorithm, if the energy change in flipping a spin is zero, , then the spin would flip with probability . Similarly, if the temperature is very high, then and again, the probability of a flip is one-half. If the temperature is very low, then a flip to a higher-energy state almost never happens, while a flip to a lower energy state almost always happens.
Comparison to Metropolis
 The Glauber algorithm can be compared to the
The Glauber algorithm can be compared to the Metropolis–Hastings algorithm
In statistics and statistical physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo (MCMC) method for obtaining a sequence of random samples from a probability distribution from which direct sampling is difficult. New sample ...
. These two differ in how a spin site is selected (step 1), and in the probability of a spin-flip (step 4). In the Glauber dynamic, every spin has an equal chance of being chosen at each time step, and the decision to flip that spin, or not, is given by the Fermi function
Enrico Fermi (; 29 September 1901 – 28 November 1954) was an Italian and naturalized American physicist, renowned for being the creator of the world's first artificial nuclear reactor, the Chicago Pile-1, and a member of the Manhattan Project ...
, as given above.
By contrast, the Metropolis algorithm considers a spin site with a probability given by the Boltzmann weight , but if it is accepted, then it always flips a spin in favor of lowering the energy. Thus, the total spin-flip probability is:
:
 Although both of the acceptance probabilities approximate a step curve and they are almost indistinguishable at very low temperatures, they differ when temperature gets high. For an Ising model on a 2d lattice, the critical temperature is .
At thermal equilibrium, the Glauber and Metropolis algorithms should give identical results. In general, at equilibrium, any MCMC algorithm should produce the same distribution, as long as the algorithm satisfies
Although both of the acceptance probabilities approximate a step curve and they are almost indistinguishable at very low temperatures, they differ when temperature gets high. For an Ising model on a 2d lattice, the critical temperature is .
At thermal equilibrium, the Glauber and Metropolis algorithms should give identical results. In general, at equilibrium, any MCMC algorithm should produce the same distribution, as long as the algorithm satisfies ergodicity
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies th ...
and detailed balance
The principle of detailed balance can be used in Kinetics (physics), kinetic systems which are decomposed into elementary processes (collisions, or steps, or elementary reactions). It states that at Thermodynamic equilibrium, equilibrium, each elem ...
. In both algorithms, for any change in energy, , meaning that transition between the states of the system is always possible despite being very unlikely at some temperatures. So, the condition for ergodicity is satisfied for both of the algorithms. Detailed balance, which is a requirement of reversibility, states that if you observe the system for a long enough time, the system goes from state to with the same frequency as going from to . In equilibrium, the probability of observing the system at state A is given by the Boltzmann weight, . So, the amount of time the system spends in low energy states is larger than in high energy states and there is more chance that the system is observed in states where it spends more time. Meaning that when the transition from to is energetically unfavorable, the system happens to be at more frequently, counterbalancing the lower intrinsic probability of transition. Therefore, both, Glauber and Metropolis–Hastings algorithms exhibit detailed balance.
Software
* Simulation package IsingLenzMC provides simulation of Glauber Dynamics on 1D lattices with external fieldCRAN
Related pages
* Metropolis algorithm *Ising model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that r ...
* Monte Carlo algorithm
In computing, a Monte Carlo algorithm is a randomized algorithm whose output may be incorrect with a certain (typically small) probability. Two examples of such algorithms are the Karger–Stein algorithm and the Monte Carlo algorithm for mini ...
* Simulated annealing
Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. ...
References