The shoelace formula, shoelace algorithm, or shoelace method (also known as Gauss's area formula and the surveyor's formula)
is a mathematical
algorithm to determine the
area of a
simple polygon whose vertices are described by their
Cartesian coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
in the plane.
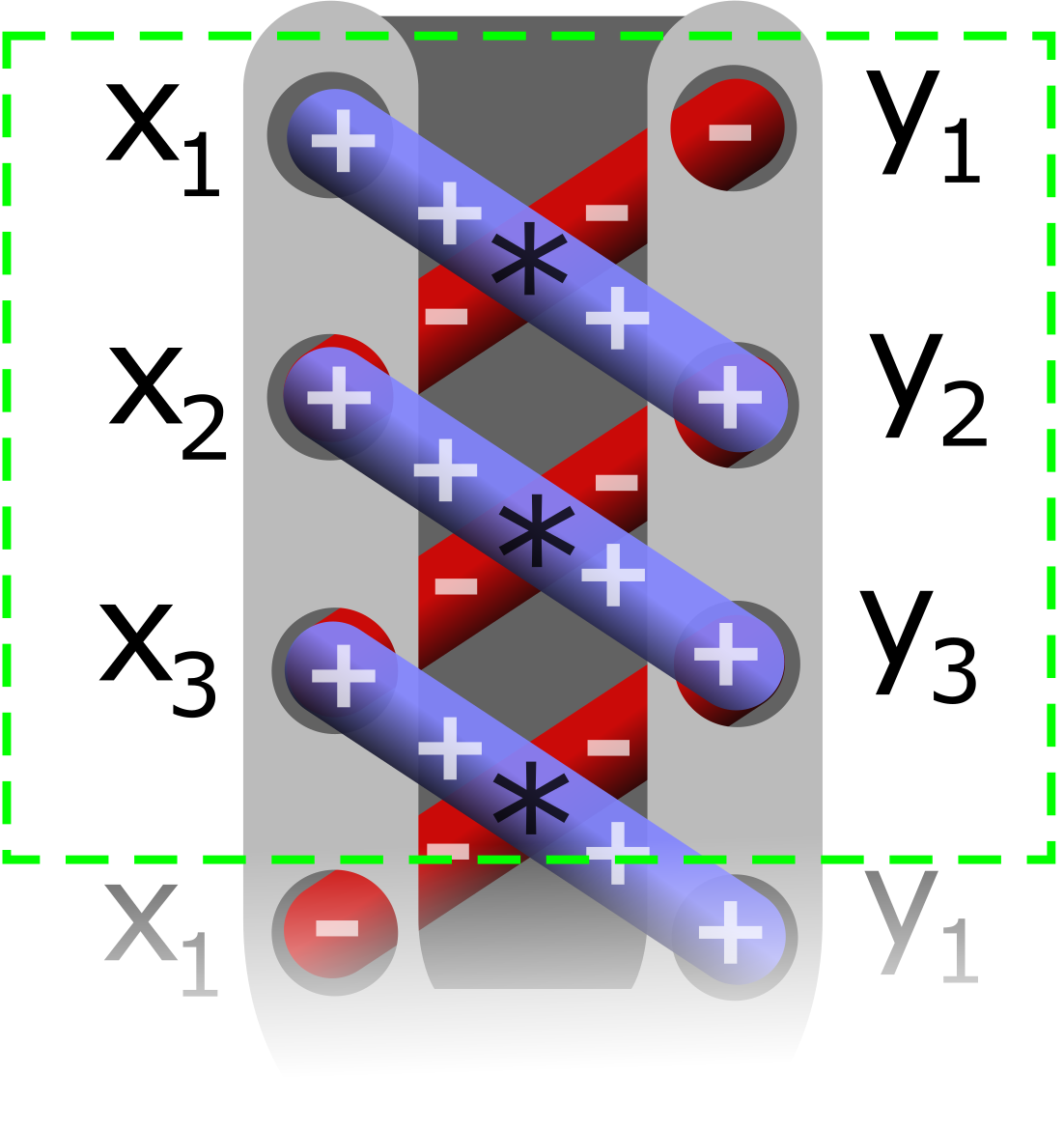
It is called the shoelace formula because of the constant cross-multiplying for the coordinates making up the polygon, like threading shoelaces.
It has applications in surveying and forestry,
[Hans Pretzsch, ]
Forest Dynamics, Growth and Yield: From Measurement to Model
', Springer, 2009, , p. 232. among other areas.
The formula was described by Albrecht Ludwig Friedrich Meister (1724–1788) in 1769 and is based on the trapezoid formula which was described by
Carl Friedrich Gauss and
C.G.J. Jacobi. The triangle form of the area formula can be considered to be a special case of
Green's theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region bounded by . It is the two-dimensional special case of Stokes' theorem.
Theorem
Let be a positively orient ...
.
The area formula can also be applied to self-overlapping polygons since the meaning of area is still clear even though self-overlapping polygons are not generally
simple. Furthermore, a self-overlapping polygon can have multiple "interpretations" but the Shoelace formula can be used to show that the polygon's area is the same regardless of the interpretation.
The polygon area formulas

''Given:'' A planar
simple polygon with a ''positively oriented'' (counter clock wise) sequence of points
in a
Cartesian coordinate system
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
.
For the simplicity of the formulas below it is convenient to set
.
''The formulas:''
The area of the given polygon can be expressed by a variety of formulas, which are connected by simple operations (see below):
If the polygon is ''negatively oriented'', then the result
of the formulas is negative. In any case
is the sought area of the polygon.
Trapezoid formula
The trapezoid formula sums up a sequence of oriented areas
of
trapezoids with
as one of its four edges (see below):
Triangle formula
The triangle formula sums up the oriented areas
of triangles
:
Shoelace formula

The determinant formulas are the base of the popular ''shoelace formula'', which is a scheme, that optimizes the calculation of the sum of the 2×2-Determinants by hand:
Other formulas
A particularly concise statement of the formula can be given in terms of the
exterior algebra. If
are the
consecutive vertices of the polygon (regarded as vectors in
the Cartesian plane) then


Example
For the area of the pentagon with
one gets
The advantage of the shoelace form: Only 6 columns have to be written for calculating the 5 determinants with 10 columns.
Deriving the formulas
Trapezoid formula

The edge
determines the trapezoid
with its oriented area
:
In case of
 The shoelace formula, shoelace algorithm, or shoelace method (also known as Gauss's area formula and the surveyor's formula) is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their
The shoelace formula, shoelace algorithm, or shoelace method (also known as Gauss's area formula and the surveyor's formula) is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their  ''Given:'' A planar simple polygon with a ''positively oriented'' (counter clock wise) sequence of points in a
''Given:'' A planar simple polygon with a ''positively oriented'' (counter clock wise) sequence of points in a  The determinant formulas are the base of the popular ''shoelace formula'', which is a scheme, that optimizes the calculation of the sum of the 2×2-Determinants by hand:
The determinant formulas are the base of the popular ''shoelace formula'', which is a scheme, that optimizes the calculation of the sum of the 2×2-Determinants by hand:


 The edge determines the trapezoid with its oriented area
:
In case of
The edge determines the trapezoid with its oriented area
:
In case of
 The shoelace formula, shoelace algorithm, or shoelace method (also known as Gauss's area formula and the surveyor's formula) is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their
The shoelace formula, shoelace algorithm, or shoelace method (also known as Gauss's area formula and the surveyor's formula) is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their  The determinant formulas are the base of the popular ''shoelace formula'', which is a scheme, that optimizes the calculation of the sum of the 2×2-Determinants by hand:
The determinant formulas are the base of the popular ''shoelace formula'', which is a scheme, that optimizes the calculation of the sum of the 2×2-Determinants by hand: