Full State Feedback on:
[Wikipedia]
[Google]
[Amazon]
Full state feedback (FSF), or pole placement, is a method employed in
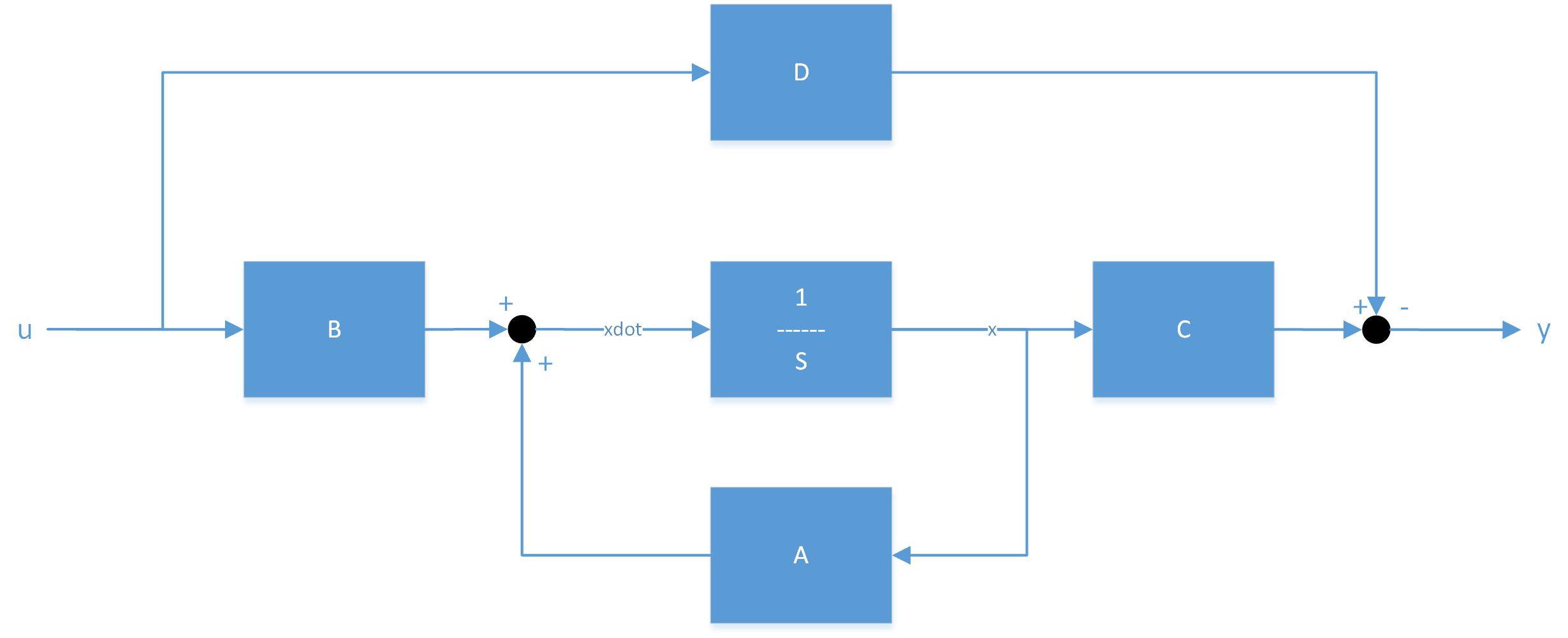 If the closed-loop dynamics can be represented by the state space equation (see
If the closed-loop dynamics can be represented by the state space equation (see  :.
Substituting into the state space equations above, we have
:
:
The poles of the FSF system are given by the characteristic equation of the matrix , . Comparing the terms of this equation with those of the desired characteristic equation yields the values of the feedback matrix which force the closed-loop eigenvalues to the pole locations specified by the desired characteristic equation.
:.
Substituting into the state space equations above, we have
:
:
The poles of the FSF system are given by the characteristic equation of the matrix , . Comparing the terms of this equation with those of the desired characteristic equation yields the values of the feedback matrix which force the closed-loop eigenvalues to the pole locations specified by the desired characteristic equation.Control Design Using Pole Placement
/ref>
Mathematica function to compute the state feedback gains
Control theory Feedback
feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause and effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handle ...
control system theory to place the closed-loop poles of a plant
Plants are the eukaryotes that form the Kingdom (biology), kingdom Plantae; they are predominantly Photosynthesis, photosynthetic. This means that they obtain their energy from sunlight, using chloroplasts derived from endosymbiosis with c ...
in predetermined locations in the s-plane.* Placing poles is desirable because the location of the poles corresponds directly to the eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s of the system, which control the characteristics of the response of the system. The system must be considered controllable in order to implement this method.
Principle
 If the closed-loop dynamics can be represented by the state space equation (see
If the closed-loop dynamics can be represented by the state space equation (see State space (controls)
In control engineering and system identification, a state-space representation is a mathematical model of a physical system that uses state variables to track how inputs shape system behavior over time through first-order differential equation ...
)
:
with output equation
:
then the poles of the system transfer function are the roots of the characteristic equation given by
:
Full state feedback is utilized by commanding the input vector . Consider an input proportional (in the matrix sense) to the state vector,
 :.
Substituting into the state space equations above, we have
:
:
The poles of the FSF system are given by the characteristic equation of the matrix , . Comparing the terms of this equation with those of the desired characteristic equation yields the values of the feedback matrix which force the closed-loop eigenvalues to the pole locations specified by the desired characteristic equation.
:.
Substituting into the state space equations above, we have
:
:
The poles of the FSF system are given by the characteristic equation of the matrix , . Comparing the terms of this equation with those of the desired characteristic equation yields the values of the feedback matrix which force the closed-loop eigenvalues to the pole locations specified by the desired characteristic equation./ref>
Example of FSF
Consider a system given by the following state space equations: : The uncontrolled system has open-loop poles at and . These poles are the eigenvalues of the matrix and they are the roots of . Suppose, for considerations of the response, we wish the controlled system eigenvalues to be located at and , which are not the poles we currently have. The desired characteristic equation is then , from . Following the procedure given above, the FSF controlled system characteristic equation is : where : Upon setting this characteristic equation equal to the desired characteristic equation, we find :. Therefore, setting forces the closed-loop poles to the desired locations, affecting the response as desired. This only works for Single-Input systems. Multiple input systems will have a matrix that is not unique. Choosing, therefore, the best values is not trivial. A linear-quadratic regulator might be used for such applications.See also
* Pole splitting * Step response * Ackermann's Formula * Linear-quadratic regulatorReferences
{{reflistExternal links
Mathematica function to compute the state feedback gains
Control theory Feedback