Fractional Anisotropy

Fractional anisotropy (FA) is a scalar value between zero and one that describes the degree of anisotropy of a diffusion process. A value of zero means that diffusion is isotropic, i.e. it is unrestricted (or equally restricted) in all directions. A value of one means that diffusion occurs only along one axis and is fully restricted along all other directions. FA is a measure often used in diffusion imaging where it is thought to reflect fiber density, axonal diameter, and myelination in white matter. The FA is an extension of the concept of eccentricity of conic sections in 3 dimensions, normalized to the unit range.

Definition

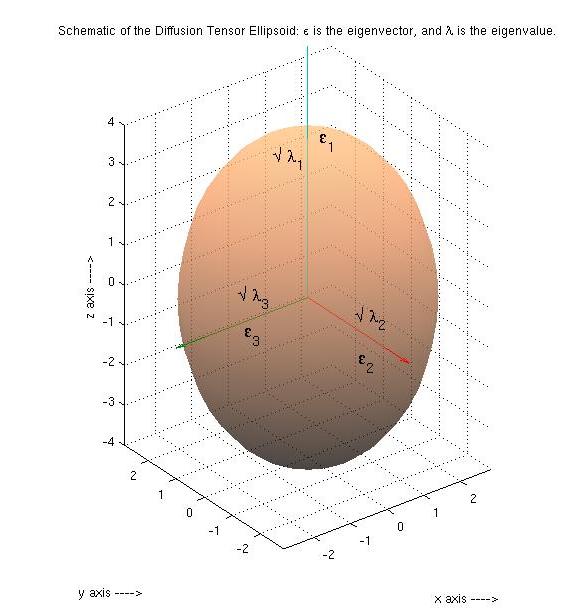
A Diffusion Ellipsoid is completely represented by the Diffusion Tensor, D. FA is calculated from the eigenvalues $\lambda_1 \ge \lambda_2 \ge \lambda_3$ of the diffusion tensor. The eigenvectors give the directions in which the ellipsoid has major axes, and the corresponding eigenvalues give the magnitude of the peak in each eigenvector direction.

: $\text = \sqrt$

with $\hat = (\lambda_1 + \lambda_2 + \lambda_3)/3$ being the mean value of the eigenvalues.

An equivalent formula for FA is

: $\text = \sqrt,$

which is further equivalent to:

: $\text = \sqrt$

where R is the "normalized" diffusion tensor:

: $\text = \frac$

Note that if all the eigenvalues are equal, which happens for isotropic (spherical) diffusion, as in free water, the FA is . The FA can reach a maximum value of (this rarely happens in real data), in which case D has only one nonzero eigenvalue and the ellipsoid reduces to a line in the direction of that eigenvector. This means that the diffusion is confined to that direction alone.

Details

This can be visualized with an ellipsoid, which is defined by the eigenvectors and eigenvalues of D. The FA of a sphere is ''0'' since the diffusion is isotropic, and there is equal probability of diffusion in all directions. The eigenvectors and eigenvalues of the Diffusion Tensor give a complete representation of the diffusion process. FA quantifies the pointedness of the ellipsoid, but does not give information about which direction it is pointing to.

Note that the FA of most liquids, including water, is unless the diffusion process is being constrained by structures such as network of fibers. The measured FA may depend on the effective length scale of the diffusion measurement. If the diffusion process is not constrained on the scale being measured (the constraints are too far apart) or the constraints switch direction on a smaller scale than the measured one, then the measured FA will be attenuated. For example, the brain can be thought of as a fluid permeated by many fibers (nerve axons). However, in most parts the fibers go in all directions, and thus although they constrain the diffusion the FA is . In some regions, such as the corpus callosum the fibers are aligned over a large enough scale (on the order of a mm) for their directions to mostly agree within the resolution element of a magnetic resonance image, and it is these regions that stand out in an FA image. Liquid crystals can also exhibit anisotropic diffusion because the needle or plate-like shapes of their molecules affect how they slide over one another. When the FA is 0 the tensor nature of D is often ignored, and it is called the diffusion constant.

File:Ellipsoid2722.jpg, FA value of 0.7698, the DT matrix is diagonal( 0 2 2
File:Ellipsoid888.jpg, FA value of 0, the DT matrix is diagonal( 4 4
File:Ellipsoid eigenvalues14142.jpg, FA value of 0.6030, the DT matrix is diagonal( 4 2

One drawback of the Diffusion Tensor model is that it can account only for Gaussian diffusion processes, which has been found to be inadequate in accurately representing the true diffusion process in the human brain. Due to this, higher order models using spherical harmonics and Orientation Distribution Functions (ODF) have been used to define newer and richer estimates of the anisotropy, called Generalized Fractional Anisotropy. GFA computations use samples of the ODF to evaluate the anisotropy in diffusion. They can also be easily calculated by using the Spherical Harmonic coefficients of the ODF model.

References

{{reflist, refs=
Basser, P.J. & Pierpaoli, C. (1996). "Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI". ''Journal of Magnetic Resonance, Series B'', 111, 209-219.

Özarslan, E. Vemuri, B.C. & Mareci, T. H. (2005). "Generalized scalar measures for diffusion MRI using trace, variance, and entropy". ''Magnetic Resonance in Medicine, '', 53, 866-876.

J. Cohen-Adad, M. Descoteaux, S. Rossignol, RD Hoge, R. Deriche, and H. Benali (2008). "Detection of multiple pathways in the spinal cord using q-ball imaging". ''NeuroImage'', 42, 739-749.

Transport phenomena
Diffusion
Imaging
Tensors
Neuroimaging
Medical imaging
Magnetic resonance imaging

de:Diffusivität#Fraktionale Anisotropie