Five Number Summary on:
[Wikipedia]
[Google]
[Amazon]
The five-number summary is a set of
import numpy as np
def fivenum(data):
"""Five-number summary."""
return np.percentile(data, , 25, 50, 75, 100 method="midpoint")
>>> moons = , 0, 1, 2, 63, 61, 27, 13>>> print(fivenum(moons))
0. 0.5 7.5 44. 63.
data fivenum;
input x @@;
datalines;
1 2 3 4 20 202 392 4 38 20
;
run;
ods select Quantiles;
proc univariate data = fivenum;
output out = fivenums min = min Q1 = Q1 Q2 = median Q3 = Q3 max = max;
run;
proc print data = fivenums;
run;
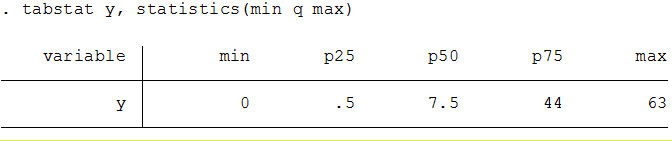
input byte y
0
0
1
2
63
61
27
13
end
list
tabstat y, statistics (min q max)
descriptive statistics
A descriptive statistic (in the count noun sense) is a summary statistic that quantitatively describes or summarizes features from a collection of information, while descriptive statistics (in the mass noun sense) is the process of using and an ...
that provides information about a dataset. It consists of the five most important sample percentile
In statistics, a ''k''-th percentile, also known as percentile score or centile, is a score (e.g., a data point) a given percentage ''k'' of all scores in its frequency distribution exists ("exclusive" definition) or a score a given percentage ...
s:
# the sample minimum ''(smallest observation)''
# the lower quartile or ''first quartile''
# the median
The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “ ...
(the middle value)
# the upper quartile or ''third quartile''
# the sample maximum (largest observation)
In addition to the median of a single set of data there are two related statistics called the upper and lower quartiles. If data are placed in order, then the lower quartile is central to the lower half of the data and the upper quartile is central to the upper half of the data. These quartiles are used to calculate the interquartile range, which helps to describe the spread of the data, and determine whether or not any data points are outliers.
In order for these statistics to exist, the observations must be from a univariate
In mathematics, a univariate object is an expression (mathematics), expression, equation, function (mathematics), function or polynomial involving only one Variable (mathematics), variable. Objects involving more than one variable are ''wikt:multi ...
variable that can be measured on an ordinal, interval or ratio scale.
Use and representation
The five-number summary provides a concise summary of the distribution of the observations. Reporting five numbers avoids the need to decide on the most appropriate summary statistic. The five-number summary gives information about the location (from the median), spread (from the quartiles) and range (from the sample minimum and maximum) of the observations. Since it reportsorder statistic
In statistics, the ''k''th order statistic of a statistical sample is equal to its ''k''th-smallest value. Together with Ranking (statistics), rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and ...
s (rather than, say, the mean) the five-number summary is appropriate for ordinal measurements, as well as interval and ratio measurements.
It is possible to quickly compare several sets of observations by comparing their five-number summaries, which can be represented graphically using a boxplot.
In addition to the points themselves, many L-estimator
In statistics, an L-estimator (or L-statistic) is an estimator which is a linear combination of order statistics of the measurements. This can be as little as a single point, as in the median (of an odd number of values), or as many as all points ...
s can be computed from the five-number summary, including interquartile range
In descriptive statistics, the interquartile range (IQR) is a measure of statistical dispersion, which is the spread of the data. The IQR may also be called the midspread, middle 50%, fourth spread, or H‑spread. It is defined as the differen ...
, midhinge, range, mid-range, and trimean.
The five-number summary is sometimes represented as in the following table:
Example
This example calculates the five-number summary for the following set of observations: 0, 0, 1, 2, 63, 61, 27, 13. These are the number of moons of each planet in theSolar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Sola ...
.
It helps to put the observations in ascending order: 0, 0, 1, 2, 13, 27, 61, 63. There are eight observations, so the median is the mean of the two middle numbers, (2 + 13)/2 = 7.5. Splitting the observations either side of the median gives two groups of four observations. The median of the first group is the lower or first quartile, and is equal to (0 + 1)/2 = 0.5. The median of the second group is the upper or third quartile, and is equal to (27 + 61)/2 = 44.
The smallest and largest observations are 0 and 63.
So the five-number summary would be 0, 0.5, 7.5, 44, 63.
Example in R
It is possible to calculate the five-number summary in theR programming language
R is a programming language for statistical computing and data visualization. It has been widely adopted in the fields of data mining, bioinformatics, data analysis, and data science.
The core R language is extended by a large number of so ...
using the fivenum function. The summary function, when applied to a vector, displays the five-number summary together with the mean (which is not itself a part of the five-number summary). The fivenum uses a different method to calculate percentiles than the summary function.
Example in Python
This python example uses thepercentile function from the numerical library numpy and works in Python 2 and 3.
Example in SAS
You can usePROC UNIVARIATE in SAS to get the five number summary:
Example in Stata
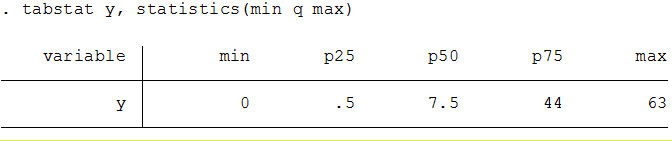
See also
*Seven-number summary In descriptive statistics, the seven-number summary is a collection of seven summary statistics, and is an extension of the five-number summary. There are three similar, common forms.
As with the five-number summary, it can be represented by a m ...
* Three-point estimation
* Box plot
In descriptive statistics, a box plot or boxplot is a method for demonstrating graphically the locality, spread and skewness groups of numerical data through their quartiles.
In addition to the box on a box plot, there can be lines (which are ca ...
References
* * {{refend Summary statistics Articles with example Python (programming language) code Articles with example R code