Finite Volume Method For Two Dimensional Diffusion Problem on:
[Wikipedia]
[Google]
[Amazon]
The methods used for solving two dimensional
is the Diffusion coefficient and is the Source term. A portion of the two dimensional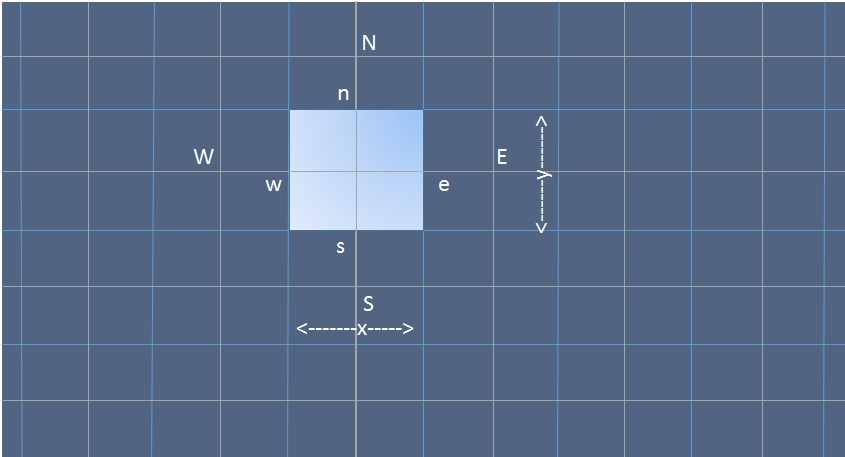 In addition to the east (E) and west (W) neighbors, a general grid node P, now also has north (N) and south (S) neighbors. The same notation is used
here for all faces and cell dimensions as in one dimensional analysis. When the above equation is formally integrated over the
In addition to the east (E) and west (W) neighbors, a general grid node P, now also has north (N) and south (S) neighbors. The same notation is used
here for all faces and cell dimensions as in one dimensional analysis. When the above equation is formally integrated over the
Finite volume method, Cheng Long
Finite volume method, Robert Eymard et al. (2010), Scholarpedia,5(6):9835
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical p ...
problems are similar to those used for one dimensional problems. The general equation for steady diffusion can be easily derived from the general transport equation for property ''Φ'' by deleting transient and convective terms
where,is the Diffusion coefficient and is the Source term. A portion of the two dimensional
grid
Grid, The Grid, or GRID may refer to:
Space partitioning
* Regular grid, a tessellation of space with translational symmetry, typically formed from parallelograms or higher-dimensional analogs
** Grid graph, a graph structure with nodes connec ...
used for Discretization
In applied mathematics, discretization is the process of transferring continuous functions, models, variables, and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numeri ...
is shown below:
 In addition to the east (E) and west (W) neighbors, a general grid node P, now also has north (N) and south (S) neighbors. The same notation is used
here for all faces and cell dimensions as in one dimensional analysis. When the above equation is formally integrated over the
In addition to the east (E) and west (W) neighbors, a general grid node P, now also has north (N) and south (S) neighbors. The same notation is used
here for all faces and cell dimensions as in one dimensional analysis. When the above equation is formally integrated over the Control volume
In continuum mechanics and thermodynamics, a control volume (CV) is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a fictitious region of a given v ...
, we obtain
Using the divergence theorem, the equation can be rewritten as :
This equation represents the balance of generation of the property φ in a Control volume
In continuum mechanics and thermodynamics, a control volume (CV) is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a fictitious region of a given v ...
and the flux
Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications in physics. For transport phe ...
es through its cell faces. The derivatives can by represented as follows by using Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
approximation:
Flux across the east face =
Flux across the south face =
Flux across the north face =
Substituting these expressions in equation (2) we obtain
When the source term is represented in linearized form ,
this equation can be rearranged as,
=
This equation can now be expressed in a general discretized equation form for internal nodes, i.e.,
Where,
The face areas in y two dimensional case are :
and
.
We obtain the distribution of the property i.e. a given two dimensional situation by writing discretized equations of the form of equation (3) at each grid node of the subdivided domain. At the boundaries where the temperature or fluxes are known the discretized equation are modified to incorporate the boundary conditions
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satis ...
. The boundary side coefficient is set to zero (cutting the link with the boundary) and the flux crossing this boundary is introduced as a source which is appended to any existing and terms. Subsequently the resulting set of equations is solved to obtain the two dimensional distribution of the property
References
* Patankar, Suhas V. (1980), Numerical Heat Transfer and Fluid Flow, Hemisphere. * Hirsch, C. (1990), Numerical Computation of Internal and External Flows, Volume 2: Computational Methods for Inviscid and Viscous Flows, Wiley. * Laney, Culbert B.(1998), Computational Gas Dynamics, Cambridge University Press. * LeVeque, Randall(1990), Numerical Methods for Conservation Laws, ETH Lectures in Mathematics Series, Birkhauser-Verlag. * Tannehill, John C., et al., (1997), Computational Fluid mechanics and Heat Transfer, 2nd Ed., Taylor and Francis. * Wesseling, Pieter(2001), Principles of Computational Fluid Dynamics, Springer-Verlag. * Carslaw, H. S. and Jager, J. C. (1959). Conduction of Heat in Solids. Oxford: Clarendon Press * Crank, J. (1956). The Mathematics of Diffusion. Oxford: Clarendon Press * Thambynayagam, R. K. M (2011). The Diffusion Handbook: Applied Solutions for Engineers: McGraw-HillExternal links
* http://opencourses.emu.edu.tr/course/view.php?id=27&lang=en * https://web.archive.org/web/20120303230200/http://nptel.iitm.ac.in/courses/112105045/ * http://ingforum.haninge.kth.se/armin/CFD/dirCFD.htm {{Webarchive, url=https://web.archive.org/web/20120713003851/http://ingforum.haninge.kth.se/armin/CFD/dirCFD.htm , date=2012-07-13Finite volume method, Cheng Long
Finite volume method, Robert Eymard et al. (2010), Scholarpedia,5(6):9835
See also
*Computational fluid dynamics
Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid dynamics, fluid flows. Computers are used to perform the calculations required ...
* Finite difference
A finite difference is a mathematical expression of the form . Finite differences (or the associated difference quotients) are often used as approximations of derivatives, such as in numerical differentiation.
The difference operator, commonly d ...
* Heat equation
In mathematics and physics (more specifically thermodynamics), the heat equation is a parabolic partial differential equation. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quanti ...
* Fokker–Planck equation
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag (physi ...
* Fick's laws of diffusion
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second ...
* Maxwell–Stefan equation
*Diffusion equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's l ...
* Convection–diffusion equation
The convection–diffusion equation is a parabolic partial differential equation that combines the diffusion equation, diffusion and convection (advection equation, advection) equations. It describes physical phenomena where particles, energy, or o ...
Computational fluid dynamics