False Diffusion on:
[Wikipedia]
[Google]
[Amazon]
False diffusion is a type of error observed when the
 In figure 1, ''u'' = 2 and ''v'' = 2 m/s everywhere so the
In figure 1, ''u'' = 2 and ''v'' = 2 m/s everywhere so the
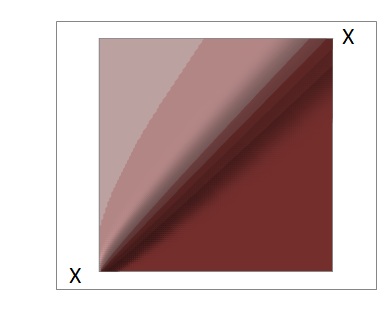 In this case, heat from west and south walls is carried by
In this case, heat from west and south walls is carried by




 ''SUCCA'' takes the local flow direction into account by introducing the influence of upwind corner cells into the discretized conservation equation in the general governing transport equation. In Fig 5, ''SUCCA'' is applied within nine cell grid cluster. Considering the SW corner inflow for cell P, the ''SUCCA'' equations for the convective transport of the conserved species are
i.e.,
i.e.,
This formulation satisfies all the criteria of
''SUCCA'' takes the local flow direction into account by introducing the influence of upwind corner cells into the discretized conservation equation in the general governing transport equation. In Fig 5, ''SUCCA'' is applied within nine cell grid cluster. Considering the SW corner inflow for cell P, the ''SUCCA'' equations for the convective transport of the conserved species are
i.e.,
i.e.,
This formulation satisfies all the criteria of  In Fig. 6, as mesh is refined, the ''upwind scheme'' gives more accurate results but ''SUCCA'' offers a nearly exact solution and is more useful in avoiding multidimensional false diffusion errors.
In Fig. 6, as mesh is refined, the ''upwind scheme'' gives more accurate results but ''SUCCA'' offers a nearly exact solution and is more useful in avoiding multidimensional false diffusion errors.
upwind scheme
In computational physics, the term advection scheme refers to a class of numerical discretization methods for solving hyperbolic partial differential equations. In the so-called upwind schemes ''typically'', the so-called upstream variables are use ...
is used to approximate the convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoy ...
term in convection–diffusion equation
The convection–diffusion equation is a parabolic partial differential equation that combines the diffusion equation, diffusion and convection (advection equation, advection) equations. It describes physical phenomena where particles, energy, or o ...
s. The more accurate central difference scheme
In applied mathematics, the central differencing scheme is a finite difference method that optimizes the approximation for the differential operator in the central node of the considered patch and provides numerical solutions to differential equa ...
can be used for the convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoy ...
term, but for grids with cell Peclet number more than 2, the central difference scheme is unstable and the simpler upwind scheme is often used. The resulting error from the upwind differencing scheme has a diffusion-like appearance in two- or three-dimensional co-ordinate systems and is referred as "false diffusion". False-diffusion errors in numerical solutions of convection-diffusion problems, in two- and three-dimensions, arise from the numerical approximations of the convection term in the conservation equations. Over the past 20 years many numerical techniques have been developed to solve convection-diffusion equations and none are problem-free, but false diffusion is one of the most serious problems and a major topic of controversy and confusion among numerical analysts
Numerical may refer to:
* Number
* Numerical digit
* Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical ...
.
Definition
False diffusion is defined as an error having a diffusion-like appearance, obtained when the ''upwind scheme'' is used in multidimensional cases to solve for the distribution of transported properties flowing non-orthogonally to one or more of the system's major axes. The error is absent when the flow is orthogonal or parallel to each major axis.Example
 In figure 1, ''u'' = 2 and ''v'' = 2 m/s everywhere so the
In figure 1, ''u'' = 2 and ''v'' = 2 m/s everywhere so the velocity field
In continuum mechanics the flow velocity in fluid dynamics, also macroscopic velocity in statistical mechanics, or drift velocity in electromagnetism, is a vector field used to mathematically describe the motion of a continuum. The length of the f ...
is uniform and perpendicular to the diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek � ...
(XX). The boundary conditions for temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
on north and west wall is 100 ̊C and for east and south wall is 0 ̊C. This region is meshed into 10×10 equal grids. Take two cases, (i) with diffusion coefficient
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurate ...
≠ 0 and, case (ii) with diffusion coefficient = 0.
Case (i)
 In this case, heat from west and south walls is carried by
In this case, heat from west and south walls is carried by convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoy ...
flow towards north and east walls. Heat is also diffused across the diagonal XX from upper to lower triangle. Figure 2 shows the approximate temperature distribution.
Case (ii)
In this case heat from west and south walls is convected by flow towards north and east. There will be no diffusion across the diagonal XX but, when the upwind scheme is applied the results are similar to case (i) where actual diffusion is occurring. This error is known as false diffusion.Background
In early approaches,derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
s in the ''differential form
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications ...
'' of the governing '' transport equation'' were replaced by finite difference approximations, usually central differencing approximations with second order accuracy. However, for large Peclet numbers (generally > 2) this approximation gave inaccurate results. It was recognized independently by several investigators that the less expensive but only first order accurate ''upwind scheme'' can be employed but that this scheme produces results with false diffusion for multidimensional cases. Many new schemes have been developed to counter false diffusion but a reliable, accurate and economical discretisation scheme is still unavailable.
Reducing errors




Finer mesh
False diffusion with the ''upwind scheme'' is reduced by increasing the mesh density. In the results of figure 3 and 4 the false diffusion error is lowest in figure 4(b) with finer mesh size.Other schemes
False diffusion error also can be reduced by using schemes such as the '' power law scheme'', ''QUICK scheme
In computational fluid dynamics QUICK, which stands for Quadratic Upstream Interpolation for Convective Kinematics, is a higher-Orders of approximation, order differencing scheme that considers a three-point upstream weighted by quadratic interpola ...
'', ''exponential scheme'', and ''SUCCA'', and others.
Improving the upwind scheme
False diffusion with the simple ''upwind scheme'' occurs because the scheme does not take into account grid/flow direction inclination. An approximate expression for the false-diffusion term in two dimensions has been given by de Vahl Davis and Mallinson(1972) where ''U'' is the resultant velocity and ''θ'' is the angle made by the velocity vector with the ''x'' direction. False diffusion is absent when the resultant flow is aligned with either of the sets of grid lines and is greatest when the flow direction is 45˚ to the grid lines.Determining the accuracy of approximation for the convection term
Using ''Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
'' for and at the time ''t'' + ''kt'' are
according to the upwind approximation for convection (UAC),. Neglecting the higher order in equation (2a), the error of convected flux due to this approximation is . It has the form of flux of by false diffusion with a diffusion co-efficient
The subscript ''fc'' is a reminder that this is a false diffusion arising from the estimate of the convected flux at the instant using UAC.
''Skew upwind corner convection algorithm'' (''SUCCA'')
 ''SUCCA'' takes the local flow direction into account by introducing the influence of upwind corner cells into the discretized conservation equation in the general governing transport equation. In Fig 5, ''SUCCA'' is applied within nine cell grid cluster. Considering the SW corner inflow for cell P, the ''SUCCA'' equations for the convective transport of the conserved species are
i.e.,
i.e.,
This formulation satisfies all the criteria of
''SUCCA'' takes the local flow direction into account by introducing the influence of upwind corner cells into the discretized conservation equation in the general governing transport equation. In Fig 5, ''SUCCA'' is applied within nine cell grid cluster. Considering the SW corner inflow for cell P, the ''SUCCA'' equations for the convective transport of the conserved species are
i.e.,
i.e.,
This formulation satisfies all the criteria of convergence
Convergence may refer to:
Arts and media Literature
*''Convergence'' (book series), edited by Ruth Nanda Anshen
*Convergence (comics), "Convergence" (comics), two separate story lines published by DC Comics:
**A four-part crossover storyline that ...
and stability.
 In Fig. 6, as mesh is refined, the ''upwind scheme'' gives more accurate results but ''SUCCA'' offers a nearly exact solution and is more useful in avoiding multidimensional false diffusion errors.
In Fig. 6, as mesh is refined, the ''upwind scheme'' gives more accurate results but ''SUCCA'' offers a nearly exact solution and is more useful in avoiding multidimensional false diffusion errors.
See also
*Computational fluid dynamics
Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid dynamics, fluid flows. Computers are used to perform the calculations required ...
*Navier–Stokes equations
The Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician Georg ...
*Numerical diffusion
Numerical diffusion is a difficulty with computer simulations of continua (such as fluids) wherein the simulated medium exhibits a higher diffusivity than the true medium. This phenomenon can be particularly egregious when the system should not b ...
*Finite volume method
The finite volume method (FVM) is a method for representing and evaluating partial differential equations in the form of algebraic equations.
In the finite volume method, volume integrals in a partial differential equation that contain a divergen ...
*Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
References
Further reading
* * *{{Citation , publisher = Cambridge University Press , isbn = 9780521853262 , last = Date , first = Anil W. , title = Introduction to Computational Fluid Dynamics , year = 2005 , bibcode = 2005icfd.book.....D Computational fluid dynamics Numerical differential equations Numerical artifacts