Falling Bodies

A set of equations describing the trajectories of objects subject to a constant gravitational force under normal Earth-bound conditions. Assuming constant acceleration ''g'' due to Earth's gravity, Newton's law of universal gravitation simplifies to ''F'' = ''mg'', where ''F'' is the force exerted on a mass ''m'' by the Earth's gravitational field of strength ''g''. Assuming constant ''g'' is reasonable for objects falling to Earth over the relatively short vertical distances of our everyday experience, but is not valid for greater distances involved in calculating more distant effects, such as spacecraft trajectories.

History

Galileo was the first to demonstrate and then formulate these equations. He used a ramp to study rolling balls, the ramp slowing the acceleration enough to measure the time taken for the ball to roll a known distance. He measured elapsed time with a water clock, using an "extremely accurate balance" to measure the amount of water.See the works of Stillman Drake, for a comprehensive study of Galileo and his times, the Scientific Revolution.

The equations ignore air resistance, which has a dramatic effect on objects falling an appreciable distance in air, causing them to quickly approach a terminal velocity. The effect of air resistance varies enormously depending on the size and geometry of the falling object—for example, the equations are hopelessly wrong for a feather, which has a low mass but offers a large resistance to the air. (In the absence of an atmosphere all objects fall at the same rate, as astronaut David Scott demonstrated by dropping a hammer and a feather on the surface of the Moon.)

The equations also ignore the rotation of the Earth, failing to describe the Coriolis effect for example. Nevertheless, they are usually accurate enough for dense and compact objects falling over heights not exceeding the tallest man-made structures.

Overview

Near the surface of the Earth, the acceleration due to gravity  = 9.807 m/s² (metres per second squared, which might be thought of as "metres per second, per second"; or 32.18 ft/s² as "feet per second per second") approximately. A coherent set of units for , , and is essential. Assuming SI units, is measured in metres per second squared, so must be measured in metres, in seconds and in metres per second.

In all cases, the body is assumed to start from rest, and air resistance is neglected. Generally, in Earth's atmosphere, all results below will therefore be quite inaccurate after only 5 seconds of fall (at which time an object's velocity will be a little less than the vacuum value of 49 m/s (9.8 m/s² × 5 s) due to air resistance). Air resistance induces a drag force on any body that falls through any atmosphere other than a perfect vacuum, and this drag force increases with velocity until it equals the gravitational force, leaving the object to fall at a constant terminal velocity.

Terminal velocity depends on atmospheric drag, the coefficient of drag for the object, the (instantaneous) velocity of the object, and the area presented to the airflow.

Apart from the last formula, these formulas also assume that negligibly varies with height during the fall (that is, they assume constant acceleration). The last equation is more accurate where significant changes in fractional distance from the centre of the planet during the fall cause significant changes in . This equation occurs in many applications of basic physics.

The following equations start from the general equations of linear motion:

$d(t) = d_0 + v_0 t + a t^2$

$v(t) = v_0 + a t$

and equation for universal gravitation (r+d= distance of object above the ground from the center of mass of planet):

: $F=G = m g$

Equations

Example

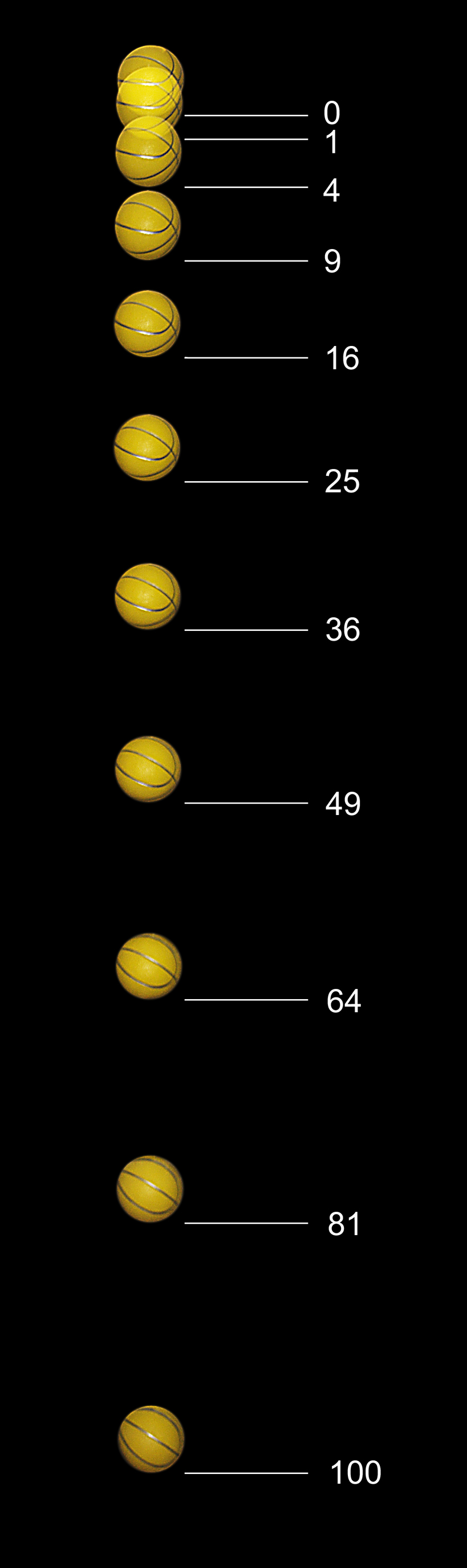
The first equation shows that, after one second, an object will have fallen a distance of 1/2 × 9.8 × 1² = 4.9 m. After two seconds it will have fallen 1/2 × 9.8 × 2² = 19.6 m; and so on. On the other hand, the penultimate equation becomes grossly inaccurate at great distances. If an object fell 10000 m to Earth, then the results of both equations differ by only 0.08%; however, if it fell from geosynchronous orbit, which is 42164 km, then the difference changes to almost 64%.

Based on wind resistance, for example, the terminal velocity of a skydiver in a belly-to-earth (i.e., face down) free-fall position is about 195 km/h (122 mph or 54 m/s). This velocity is the asymptotic limiting value of the acceleration process, because the effective forces on the body balance each other more and more closely as the terminal velocity is approached. In this example, a speed of 50% of terminal velocity is reached after only about 3 seconds, while it takes 8 seconds to reach 90%, 15 seconds to reach 99% and so on.

Higher speeds can be attained if the skydiver pulls in his or her limbs (see also freeflying). In this case, the terminal velocity increases to about 320 km/h (200 mph or 90 m/s), which is almost the terminal velocity of the peregrine falcon diving down on its prey. The same terminal velocity is reached for a typical .30-06 bullet dropping downwards—when it is returning to earth having been fired upwards, or dropped from a tower—according to a 1920 U.S. Army Ordnance study.

For astronomical bodies other than Earth, and for short distances of fall at other than "ground" level, in the above equations may be replaced by $\frac$ where is the gravitational constant, is the mass of the astronomical body, is the mass of the falling body, and is the radius from the falling object to the center of the astronomical body.

Removing the simplifying assumption of uniform gravitational acceleration provides more accurate results. We find from the formula for radial elliptic trajectories:

The time taken for an object to fall from a height to a height , measured from the centers of the two bodies, is given by:
: $t = \frac \, r^$

where $\mu = G(M + m)$ is the sum of the standard gravitational parameters of the two bodies. This equation should be used whenever there is a significant difference in the gravitational acceleration during the fall.
Note that when $x = r$ this equation gives $t = 0$, as expected; and when $x = 0$ it gives $t = \frac \sqrt$, which is the time to collision.

Acceleration relative to the rotating Earth

Centripetal force causes the acceleration measured on the rotating surface of the Earth to differ from the acceleration that is measured for a free-falling body: the apparent acceleration in the rotating frame of reference is the total gravity vector minus a small vector toward the north–south axis of the Earth, corresponding to staying stationary in that frame of reference.

See also

* '' De motu antiquiora'' and ''Two New Sciences'' (the earliest modern investigations of the motion of falling bodies)
* Equations of motion
* Free fall
* Gravity
* Mean speed theorem, the foundation of the law of falling bodies
* Radial trajectory

Notes

References

{{Reflist

External links

Falling body equations calculator

Gravity
Equations
Falling