An existential graph is a type of

diagram A diagram is a symbolic Depiction, representation of information using Visualization (graphics), visualization techniques. Diagrams have been used since prehistoric times on Cave painting, walls of caves, but became more prevalent during the Age o ...

matic or visual notation for logical expressions, created by

Charles Sanders Peirce Charles Sanders Peirce ( ; September 10, 1839 – April 19, 1914) was an American scientist, mathematician, logician, and philosopher who is sometimes known as "the father of pragmatism". According to philosopher Paul Weiss (philosopher), Paul ...

, who wrote on graphical logic as early as 1882, and continued to develop the method until his death in 1914. They include both a separate graphical notation for logical statements and a logical calculus, a formal system of rules of inference that can be used to derive theorems.

Background

Peirce found the algebraic notation (i.e. symbolic notation) of logic, especially that of predicate logic, which was still very new during his lifetime and which he himself played a major role in developing, to be philosophically unsatisfactory, because the symbols had their meaning by mere convention. In contrast, he strove for a style of writing in which the signs literally carry their meaning within them – in the terminology of his theory of signs: a system of iconic signs that resemble or resemble the represented objects and relations. Thus, the development of an iconic, graphic and – as he intended – intuitive and easy-to-learn logical system was a project that Peirce worked on throughout his life. After at least one aborted approach – the "Entitative Graphs" – the closed system of "Existential Graphs" finally emerged from 1896 onwards. Although considered by their creator to be a clearly superior and more intuitive system, as a mode of writing and as a calculus, they had no major influence on the history of logic. This has been attributed to the fact(s) that, for one, Peirce published little on this topic, and that the published texts were not written in a very understandable way; and, for two, that the linear formula notation in the hands of experts is actually the less complex tool. Hence, the existential graphs received little attention or were seen as unwieldy. From 1963 onwards, works by Don D. Roberts and J. Jay Zeman, in which Peirce's graphic systems were systematically examined and presented, led to a better understanding; even so, they have today found practical use within only one modern application—the conceptual graphs introduced by John F. Sowa in 1976, which are used in computer science to represent knowledge. However, existential graphs are increasingly reappearing as a subject of research in connection with a growing interest in graphical logic, which is also expressed in attempts to replace the rules of inference given by Peirce with more intuitive ones. The overall system of existential graphs is composed of three subsystems that build on each other, the alpha graphs, the beta graphs and the gamma graphs. The alpha graphs are a purely propositional logical system. Building on this, the beta graphs are a first order logical calculus. The gamma graphs, which have not yet been fully researched and were not completed by Peirce, are understood as a further development of the alpha and beta graphs. When interpreted appropriately, the gamma graphs cover higher-level predicate logic as well as modal logic. As late as 1903, Peirce began a new approach, the "Tinctured Existential Graphs," with which he wanted to replace the previous systems of alpha, beta and gamma graphs and combine their expressiveness and performance in a single new system. Like the gamma graphs, the "Tinctured Existential Graphs" remained unfinished. As calculi, the alpha, beta and gamma graphs are sound (i.e., all expressions derived as graphs are semantically valid). The alpha and beta graphs are also complete (i.e., all propositional or predicate-logically semantically valid expressions can be derived as alpha or beta graphs). The evidence for this was provided by J. Jay Zeman in his dissertation in 1964 (see bibliography); for alpha graphs, see also the work of White, 1984

The graphs

Peirce proposed three systems of existential graphs: * ''alpha'',

isomorphic In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...

propositional logic The propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. Sometimes, it is called ''first-order'' propositional logic to contra ...

and the

two-element Boolean algebra In mathematics and abstract algebra, the two-element Boolean algebra is the Boolean algebra whose ''underlying set'' (or universe or ''carrier'') ''B'' is the Boolean domain. The elements of the Boolean domain are 1 and 0 by convention, so that ''B ...

; * ''beta'', isomorphic to

first-order logic First-order logic, also called predicate logic, predicate calculus, or quantificational logic, is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over ...

with identity, with all formulas closed; * ''gamma'', (nearly) isomorphic to

normal modal logic In logic, a normal modal logic is a set ''L'' of modal formulas such that ''L'' contains: * All propositional tautology (logic), tautologies; * All instances of the Kripke_semantics, Kripke schema: \Box(A\to B)\to(\Box A\to\Box B) and it is closed ...

. ''Alpha'' nests in ''beta'' and ''gamma''. ''Beta'' does not nest in ''gamma'', quantified modal logic being more general than put forth by Peirce.

Alpha

The

syntax In linguistics, syntax ( ) is the study of how words and morphemes combine to form larger units such as phrases and sentences. Central concerns of syntax include word order, grammatical relations, hierarchical sentence structure (constituenc ...

is: *The blank page; *Single letters or phrases written anywhere on the page; *Any graph may be enclosed by a simple closed curve called a ''cut'' or ''sep''. A cut can be empty. Cuts can nest and concatenate at will, but must never intersect. Any well-formed part of a graph is a subgraph. The

semantics Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction betwee ...

are: *The blank page denotes Truth; *Letters, phrases, subgraphs, and entire graphs may be True or False; *To enclose a subgraph with a cut is equivalent to logical

negation In logic, negation, also called the logical not or logical complement, is an operation (mathematics), operation that takes a Proposition (mathematics), proposition P to another proposition "not P", written \neg P, \mathord P, P^\prime or \over ...

or Boolean complementation. Hence an empty cut denotes False; *All subgraphs within a given cut are tacitly conjoined. Hence the ''alpha'' graphs are a minimalist notation for sentential logic, grounded in the expressive adequacy of And and Not. The ''alpha'' graphs constitute a radical simplification of the

and the truth functors. The ''depth'' of an object is the number of cuts that enclose it. ''Rules of inference'': *Insertion - Any subgraph may be inserted into an odd numbered depth. The surrounding white page is depth 1. Depth 2 are the black letters and lines that encircle elements. Depth 3 is entering the next white area in an enclosed element. *Erasure - Any subgraph in an even numbered depth may be erased. ''Rules of equivalence'': *Double cut - A pair of cuts with nothing between them may be drawn around any subgraph. Likewise two nested cuts with nothing between them may be erased. This rule is equivalent to Boolean involution and

double negation In propositional logic, the double negation of a statement states that "it is not the case that the statement is not true". In classical logic, every statement is logically equivalent to its double negation, but this is not true in intuitionis ...

elimination. *Iteration/Deiteration – To understand this rule, it is best to view a graph as a

tree structure A tree structure, tree diagram, or tree model is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, although the chart is gen ...

having

node In general, a node is a localized swelling (a "knot") or a point of intersection (a vertex). Node may refer to: In mathematics * Vertex (graph theory), a vertex in a mathematical graph *Vertex (geometry), a point where two or more curves, lines ...

s and ancestors. Any subgraph ''P'' in node ''n'' may be copied into any node depending on ''n''. Likewise, any subgraph ''P'' in node ''n'' may be erased if there exists a copy of ''P'' in some node ancestral to ''n'' (i.e., some node on which ''n'' depends). For an equivalent rule in an algebraic context, see C2 in ''

Laws of Form ''Laws of Form'' (hereinafter ''LoF'') is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy. ''LoF'' describes three distinct logical systems: * The primary arithmetic (described in Ch ...

''. A proof manipulates a graph by a series of steps, with each step justified by one of the above rules. If a graph can be reduced by steps to the blank page or an empty cut, it is what is now called a tautology (or the complement thereof, a contradiction). Graphs that cannot be simplified beyond a certain point are analogues of the

satisfiable In mathematical logic, a formula is ''satisfiable'' if it is true under some assignment of values to its variables. For example, the formula x+3=y is satisfiable because it is true when x=3 and y=6, while the formula x+1=x is not satisfiable over ...

formula In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwe ...

s of

Beta

In the case of betagraphs, the atomic expressions are no longer propositional letters (P, Q, R,...) or statements ("It rains," "Peirce died in poverty"), but predicates in the sense of predicate logic (see there for more details), possibly abbreviated to predicate letters (F, G, H,...). A predicate in the sense of predicate logic is a sequence of words with clearly defined spaces that becomes a propositional sentence if you insert a proper noun into each space. For example, the word sequence "_ x is a human" is a predicate because it gives rise to the declarative sentence "Peirce is a human" if you enter the proper name "Peirce" in the blank space. Likewise, the word sequence "_₁ is richer than _₂" is a predicate, because it results in the statement "Socrates is richer than Plato" if the proper names "Socrates" or "Plato" are inserted into the spaces.

Notation of betagraphs

The basic language device is the line of identity, a thickly drawn line of any form. The identity line docks onto the blank space of a predicate to show that the predicate applies to at least one individual. In order to express that the predicate "_ is a human being" applies to at least one individual – i.e. to say that there is (at least) one human being – one writes an identity line in the blank space of the predicate "_ is a human being:"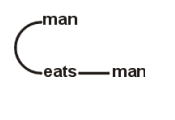 Existential graph 3

The beta graphs can be read as a system in which all formula are to be taken as closed, because all variables are implicitly quantified. If the "shallowest" part of a line of identity has even depth, the associated variable is tacitly existentially ( universally) quantified. Zeman (1964) was the first to note that the ''beta'' graphs are

with

equality Equality generally refers to the fact of being equal, of having the same value. In specific contexts, equality may refer to: Society * Egalitarianism, a trend of thought that favors equality for all people ** Political egalitarianism, in which ...

(also see Zeman 1967). However, the secondary literature, especially Roberts (1973) and Shin (2002), does not agree on how this is. Peirce's writings do not address this question, because first-order logic was first clearly articulated only after his death, in the 1928 first edition of

David Hilbert David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician and philosopher of mathematics and one of the most influential mathematicians of his time. Hilbert discovered and developed a broad range of fundamental idea ...

and

Wilhelm Ackermann Wilhelm Friedrich Ackermann (; ; 29 March 1896 – 24 December 1962) was a German mathematician and logician best known for his work in mathematical logic and the Ackermann function, an important example in the theory of computation. Biograph ...

's ''

Principles of Mathematical Logic ''Principles of Mathematical Logic'' is the 1950 American translation of the 1938 second edition of David Hilbert's and Wilhelm Ackermann's classic text ''Grundzüge der theoretischen Logik'', on elementary mathematical logic. The 1928 first edit ...

''.

Gamma

Add to the syntax of ''alpha'' a second kind of simple closed curve, written using a dashed rather than a solid line. Peirce proposed rules for this second style of cut, which can be read as the primitive

unary operator In mathematics, a unary operation is an operation with only one operand, i.e. a single input. This is in contrast to ''binary operations'', which use two operands. An example is any function , where is a set; the function is a unary operatio ...

modal logic Modal logic is a kind of logic used to represent statements about Modality (natural language), necessity and possibility. In philosophy and related fields it is used as a tool for understanding concepts such as knowledge, obligation, and causality ...

. Zeman (1964) was the first to note that the ''gamma'' graphs are equivalent to the well-known modal logics S4 and S5. Hence the ''gamma'' graphs can be read as a peculiar form of

. This finding of Zeman's has received little attention to this day, but is nonetheless included here as a point of interest.

Peirce's role

The existential graphs are a curious offspring of Peirce the

logic Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure o ...

ian/mathematician with Peirce the founder of a major strand of

semiotics Semiotics ( ) is the systematic study of sign processes and the communication of meaning. In semiotics, a sign is defined as anything that communicates intentional and unintentional meaning or feelings to the sign's interpreter. Semiosis is a ...

. Peirce's graphical logic is but one of his many accomplishments in logic and mathematics. In a series of papers beginning in 1867, and culminating with his classic paper in the 1885 ''

American Journal of Mathematics The ''American Journal of Mathematics'' is a bimonthly mathematics journal published by the Johns Hopkins University Press. History The ''American Journal of Mathematics'' is the oldest continuously published mathematical journal in the United S ...

'', Peirce developed much of the

propositional calculus The propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. Sometimes, it is called ''first-order'' propositional logic to contra ...

, quantification and the

predicate calculus Predicate or predication may refer to: * Predicate (grammar), in linguistics * Predication (philosophy) * several closely related uses in mathematics and formal logic: **Predicate (mathematical logic) ** Propositional function **Finitary relation, ...

, and some rudimentary

set theory Set theory is the branch of mathematical logic that studies Set (mathematics), sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathema ...

. Model theorists consider Peirce the first of their kind. He also extended De Morgan's

relation algebra In mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation. The motivating example of a relation algebra is the algebra 2''X'' 2 of all binary re ...

. He stopped short of

metalogic Metalogic is the metatheory of logic. Whereas ''logic'' studies how logical systems can be used to construct valid and sound arguments, metalogic studies the properties of logical systems. Logic concerns the truths that may be derived using a lo ...

(which eluded even ''

Principia Mathematica The ''Principia Mathematica'' (often abbreviated ''PM'') is a three-volume work on the foundations of mathematics written by the mathematician–philosophers Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1 ...

''). But Peirce's evolving

semiotic Semiotics ( ) is the systematic study of semiosis, sign processes and the communication of Meaning (semiotics), meaning. In semiotics, a Sign (semiotics), sign is defined as anything that communicates intentional and unintentional meaning or feel ...

theory led him to doubt the value of logic formulated using conventional linear notation, and to prefer that logic and mathematics be notated in two (or even three) dimensions. His work went beyond Euler's diagrams and Venn's 1880 revision thereof.

Frege Friedrich Ludwig Gottlob Frege (; ; 8 November 1848 – 26 July 1925) was a German philosopher, logician, and mathematician. He was a mathematics professor at the University of Jena, and is understood by many to be the father of analytic philos ...

's 1879 work ''

Begriffsschrift ''Begriffsschrift'' (German for, roughly, "concept-writing") is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book. ''Begriffsschrift'' is usually translated as ''concept writing'' or ''concept notati ...

'' also employed a two-dimensional notation for logic, but one very different from Peirce's. Peirce's first published paper on graphical logic (reprinted in Vol. 3 of his ''Collected Papers'') proposed a system dual (in effect) to the ''alpha'' existential graphs, called the

entitative graph An existential graph is a type of diagrammatic or visual notation for logical expressions, created by Charles Sanders Peirce, who wrote on graphical logic as early as 1882, and continued to develop the method until his death in 1914. They include ...

s. He very soon abandoned this formalism in favor of the existential graphs. In 1911

Victoria, Lady Welby Victoria, Lady Welby (27 April 1837 – 29 March 1912), more correctly Lady Welby-Gregory, was a self-educated British philosopher of language, musician and watercolourist. Early life Welby was born to the Hon. Charles Stuart-Wortley-Ma ...

showed the existential graphs to C. K. Ogden who felt they could usefully be combined with Welby's thoughts in a "less abstruse form." Otherwise they attracted little attention during his life and were invariably denigrated or ignored after his death, until the PhD theses by Roberts (1964) and Zeman (1964).

References

*1931–1935 & 1958. '' The Collected Papers of Charles Sanders Peirce''. Volume 4, Book II: "Existential Graphs", consists of paragraphs 347–584. A discussion also begins in paragraph 617. **Paragraphs 347–349 (II.1.1. "Logical Diagram")—Peirce's definition "Logical Diagram (or Graph)" in Baldwin's ''Dictionary of Philosophy and Psychology'' (1902)
v. 2, p. 28
''Classics in the History of Psychology'

**Paragraphs 350–371 (II.1.2. "Of Euler's Diagrams")—from "Graphs" (manuscript 479) c. 1903. **Paragraphs 372–58
Eprint
**Paragraphs 372–393 (II.2. "Symbolic Logic")—Peirce's part of "Symbolic Logic" in Baldwin's ''Dictionary of Philosophy and Psychology'' (1902
v. 2, pp. 645
��650, beginning (near second column's top) with "If symbolic logic be defined...". Paragraph 393 (Baldwin's DPP2 p. 650) is by Peirce and

Christine Ladd-Franklin Christine Ladd-Franklin (December 1, 1847 – March 5, 1930) was an American psychologist, logician, and mathematician. Early life and education Christine Ladd, sometimes known by the nickname "Kitty", was born on December 1, 1847, in Winds ...

("C.S.P., C.L.F."). **Paragraphs 394–417 (II.3. "Existential Graphs")—from Peirce's pamphlet ''A Syllabus of Certain Topics of Logic'', pp. 15–23, Alfred Mudge & Son, Boston (1903). **Paragraphs 418–509 (II.4. "On Existential Graphs, Euler's Diagrams, and Logical Algebra")—from "Logical Tracts, No. 2" (manuscript 492), c. 1903. **Paragraphs 510–529 (II.5. "The Gamma Part of Existential Graphs")—from "Lowell Lectures of 1903," Lecture IV (manuscript 467). **Paragraphs 530–572 (II.6.)—"Prolegomena To an Apology For Pragmaticism" (1906), ''

The Monist ''The Monist: An International Quarterly Journal of General Philosophical Inquiry'' is a quarterly peer-reviewed academic journal in the field of philosophy. It was established in October 1890 by American publisher Edward C. Hegeler. History Init ...

'', v. XVI
n. 4, pp. 492
546. Corrections (1907) in ''The Monist'' v. XVII
p. 160
**Paragraphs 573–584 (II.7. "An Improvement on the Gamma Graphs")—from "For the National Academy of Science, 1906 April Meeting in Washington" (manuscript 490). **Paragraphs 617–623 (at least) (in Book III, Ch. 2, §2, paragraphs 594–642)—from "Some Amazing Mazes: Explanation of Curiosity the First", ''The Monist'', v. XVIII, 1908
n. 3, pp. 416
464, see startin
p. 440
*1992. "Lecture Three: The Logic of Relatives", '' Reasoning and the Logic of Things'', pp. 146–164. Ketner, Kenneth Laine (editing and introduction), and

Hilary Putnam Hilary Whitehall Putnam (; July 31, 1926 – March 13, 2016) was an American philosopher, mathematician, computer scientist, and figure in analytic philosophy in the second half of the 20th century. He contributed to the studies of philosophy of ...

(commentary).

Harvard University Press Harvard University Press (HUP) is an academic publishing house established on January 13, 1913, as a division of Harvard University. It is a member of the Association of University Presses. Its director since 2017 is George Andreou. The pres ...

. Peirce's 1898 lectures in Cambridge, Massachusetts. *1977, 2001. '' Semiotic and Significs: The Correspondence between C.S. Peirce and Victoria Lady Welby''. Hardwick, C.S., ed. Lubbock TX: Texas Tech University Press. 2nd edition 2001.
A transcription of Peirce's MS 514
(1909), edited with commentary by John Sowa. Currently, the chronological critical edition of Peirce's works, the '' Writings'', extends only to 1892. Much of Peirce's work on

logical graph An existential graph is a type of diagrammatic or visual notation for logical expressions, created by Charles Sanders Peirce, who wrote on graphical logic as early as 1882, and continued to develop the method until his death in 1914. They include ...

s consists of manuscripts written after that date and still unpublished. Hence our understanding of Peirce's graphical logic is likely to change as the remaining 23 volumes of the chronological edition appear.

Secondary literature

* Hammer, Eric M. (1998), "Semantics for Existential Graphs," ''Journal of Philosophical Logic 27'': 489–503. * Ketner, Kenneth Laine **(1981), "The Best Example of Semiosis and Its Use in Teaching Semiotics", ''American Journal of Semiotics'' v. I, n. 1–2, pp. 47–83. Article is an introduction to existential graphs. **(1990), ''Elements of Logic: An Introduction to Peirce's Existential Graphs'', Texas Tech University Press, Lubbock, TX, 99 pages, spiral-bound. * Queiroz, João & Stjernfelt, Frederik ** (2011), "Diagrammatical Reasoning and Peircean Logic Representation", ''Semiotica'' vol. 186 (1/4). (Special issue on Peirce's diagrammatic logic.

* Roberts, Don D. **(1964), "Existential Graphs and Natural Deduction" in Moore, E. C., and Robin, R. S., eds., ''Studies in the Philosophy of C. S. Peirce, 2nd series''. Amherst MA:

University of Massachusetts Press The University of Massachusetts Press is a university press that is part of the University of Massachusetts Amherst. The press was founded in 1963, publishing scholarly books and non-fiction. The press imprint is overseen by an interdisciplinar ...

. The first publication to show any sympathy and understanding for Peirce's graphical logic. **(1973). ''The Existential Graphs of C.S. Peirce.'' John Benjamins. An outgrowth of his 1963 thesis. * Shin, Sun-Joo (2002), ''The Iconic Logic of Peirce's Graphs''. MIT Press. * Zalamea, Fernando. ''Peirce's Logic of Continuity.'' Docent Press, Boston MA. 2012. ISBN 9 780983 700494. **Part II: Peirce's Existential Graphs, pp. 76-162. * Zeman, J. J. **(1964),
The Graphical Logic of C.S. Peirce.
'' Unpublished Ph.D. thesis submitted to the

University of Chicago The University of Chicago (UChicago, Chicago, or UChi) is a Private university, private research university in Chicago, Illinois, United States. Its main campus is in the Hyde Park, Chicago, Hyde Park neighborhood on Chicago's South Side, Chic ...

. **(1967), "A System of Implicit Quantification," ''Journal of Symbolic Logic 32'': 480–504.

External links

Stanford Encyclopedia of Philosophy The ''Stanford Encyclopedia of Philosophy'' (''SEP'') is a freely available online philosophy resource published and maintained by Stanford University, encompassing both an online encyclopedia of philosophy and peer-reviewed original publication ...

Peirce's Logic
by Sun-Joo Shin and Eric Hammer. * Dau, Frithjof
Peirce's Existential Graphs --- Readings and Links.
An annotated bibliography on the existential graphs. * Gottschall, Christian

— Java applet for deriving Alpha graphs. * Liu, Xin-Wen,

(via Wayback Machine), Institute of Philosophy, Chinese Academy of Social Sciences, Beijing, PRC. * (NB. Existential graphs and

conceptual graph A conceptual graph (CG) is a formalism for knowledge representation. In the first published paper on CGs, John F. Sowa used them to represent the conceptual schemas used in database systems. The first book on CGs applied them to a wide range of ...

s.) * Van Heuveln, Bram,
Existential Graphs.
" Dept. of Cognitive Science,

Rensselaer Polytechnic Institute Rensselaer Polytechnic Institute (; RPI) is a private university, private research university in Troy, New York, United States. It is the oldest technological university in the English-speaking world and the Western Hemisphere. It was establishe ...

. Alpha only. * Zeman, Jay J.,
Existential Graphs
. Wit
four online papers
by Peirce. Logic Logical calculi Philosophical logic History of logic History of mathematics Charles Sanders Peirce Logical diagrams {{Diagrams in logic