Euler's Formula on:
[Wikipedia]
[Google]
[Amazon]
Euler's formula, named after
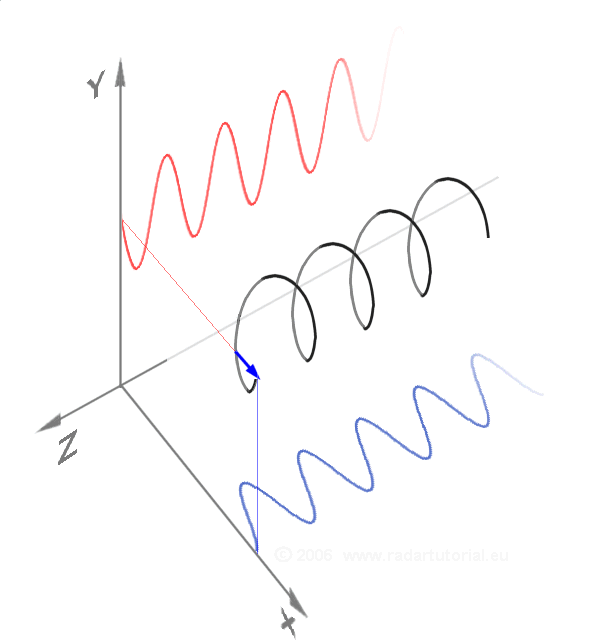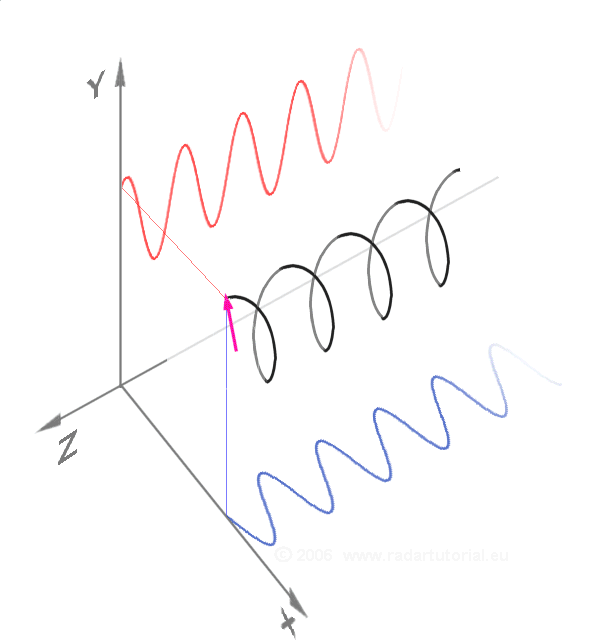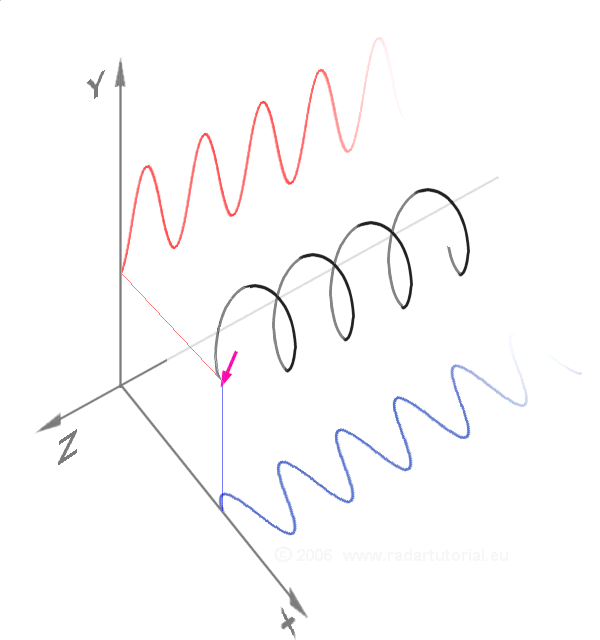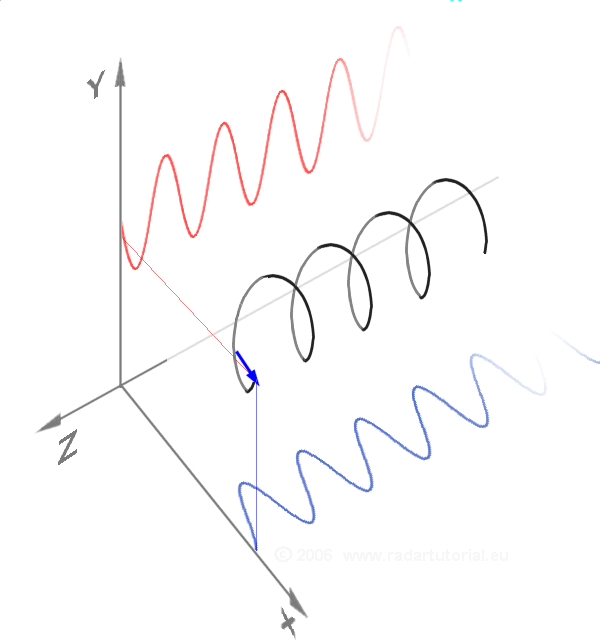 Around 1740
Around 1740
 Here is a proof of Euler's formula using power-series expansions, as well as basic facts about the powers of :
Using now the power-series definition from above, we see that for real values of
where in the last step we recognize the two terms are the Maclaurin series for and . The rearrangement of terms is justified because each series is absolutely convergent.
Here is a proof of Euler's formula using power-series expansions, as well as basic facts about the powers of :
Using now the power-series definition from above, we see that for real values of
where in the last step we recognize the two terms are the Maclaurin series for and . The rearrangement of terms is justified because each series is absolutely convergent.
 Euler's formula, the definitions of the trigonometric functions and the standard identities for exponentials are sufficient to easily derive most trigonometric identities. It provides a powerful connection between
Euler's formula, the definitions of the trigonometric functions and the standard identities for exponentials are sufficient to easily derive most trigonometric identities. It provides a powerful connection between
Elements of Algebra
{{Leonhard Euler Theorems in complex analysis Articles containing proofs Mathematical analysis E (mathematical constant) Trigonometry Leonhard Euler
Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
, is a mathematical formula in complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
that establishes the fundamental relationship between the trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
and the complex exponential function. Euler's formula states that, for any real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
, one has
where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that ...
and sine respectively. This complex exponential function is sometimes denoted ("cosine plus ''i'' sine"). The formula is still valid if is a complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
, and is also called ''Euler's formula'' in this more general case.
Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics".
When , Euler's formula may be rewritten as or , which is known as Euler's identity.
History
In 1714, the English mathematician Roger Cotes presented a geometrical argument that can be interpreted (after correcting a misplaced factor of ) as: Exponentiating this equation yields Euler's formula. Note that the logarithmic statement is not universally correct for complex numbers, since a complex logarithm can have infinitely many values, differing by multiples of . Around 1740
Around 1740 Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
turned his attention to the exponential function and derived the equation named after him by comparing the series expansions of the exponential and trigonometric expressions. The formula was first published in 1748 in his foundational work '' Introductio in analysin infinitorum''.
Johann Bernoulli
Johann Bernoulli (also known as Jean in French or John in English; – 1 January 1748) was a Swiss people, Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is known for his contributions to infin ...
had found that
And since
the above equation tells us something about complex logarithms by relating natural logarithms to imaginary (complex) numbers. Bernoulli, however, did not evaluate the integral.
Bernoulli's correspondence with Euler (who also knew the above equation) shows that Bernoulli did not fully understand complex logarithms. Euler also suggested that complex logarithms can have infinitely many values.
The view of complex numbers as points in the complex plane was described about 50 years later by Caspar Wessel.
Definitions of complex exponentiation
The exponential function for real values of may be defined in a few different equivalent ways (see Characterizations of the exponential function). Several of these methods may be directly extended to give definitions of for complex values of simply by substituting in place of and using the complex algebraic operations. In particular, we may use any of the three following definitions, which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique analytic continuation of to the complex plane.Differential equation definition
The exponential function is the unique differentiable function of a complex variable for which the derivative equals the function andPower series definition
For complex Using the ratio test, it is possible to show that this power series has an infinite radius of convergence and so defines for all complex .Limit definition
For complex Here, is restricted to positive integers, so there is no question about what the power with exponent means.Proofs
Various proofs of the formula are possible.Using differentiation
This proof shows that the quotient of the trigonometric and exponential expressions is the constant function one, so they must be equal (the exponential function is never zero, Theorem 1.42 so this is permitted). Consider the function for real . Differentiating gives by the product rule Thus, is a constant. Since the exponential function is for , by definition, and the complex trig function also evaluates to there, , then for all real , and thusUsing power series
Using polar coordinates
Another proof Second proof on page. is based on the fact that all complex numbers can be expressed inpolar coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are
*the point's distance from a reference ...
and on the assumption that can be likewise represented; this will be the case if we find a solution. Therefore, for some and depending on ,
No assumptions are being made about and ; they will be determined in the course of the proof. From any of the definitions of the exponential function it can be shown that the derivative of is . Therefore, differentiating both sides gives
Substituting for and equating real and imaginary parts in this formula gives and . Thus, is a constant, and is for some constant . We now have
knowing that , for , this becomes
giving us the constant and proving the formula
Applications
Applications in complex number theory
Interpretation of the formula
This formula can be interpreted as saying that the function is a unit complex number, i.e., it traces out theunit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
in the complex plane as ranges through the real numbers. Here is the angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
s.
The original proof is based on the Taylor series expansions of the exponential function (where is a complex number) and of and for real numbers ( see above). In fact, the same proof shows that Euler's formula is even valid for all ''complex'' numbers .
A point in the complex plane can be represented by a complex number written in cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and polar coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are
*the point's distance from a reference ...
. The polar form simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number , and its complex conjugate, , can be written as
where
* is the real part,
* is the imaginary part,
* is the magnitude of and
*.
is the argument
An argument is a series of sentences, statements, or propositions some of which are called premises and one is the conclusion. The purpose of an argument is to give reasons for one's conclusion via justification, explanation, and/or persu ...
of , i.e., the angle between the ''x'' axis and the vector ''z'' measured counterclockwise in radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
s, which is defined up to addition of . Many texts write instead of , but the first equation needs adjustment when . This is because for any real and , not both zero, the angles of the vectors and differ by radians, but have the identical value of .
Use of the formula to define the logarithm of complex numbers
Now, taking this derived formula, we can use Euler's formula to define thelogarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation):
and that
both valid for any complex numbers and . Therefore, one can write:
for any . Taking the logarithm of both sides shows that
and in fact, this can be used as the definition for the complex logarithm. The logarithm of a complex number is thus a multi-valued function, because is multi-valued.
Finally, the other exponential law
which can be seen to hold for all integers , together with Euler's formula, implies several trigonometric identities, as well as de Moivre's formula.
Relationship to trigonometry
analysis
Analysis (: analyses) is the process of breaking a complex topic or substance into smaller parts in order to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle (38 ...
and trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The fiel ...
, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:
The two equations above can be derived by adding or subtracting Euler's formulas:
and solving for either cosine or sine.
These formulas can even serve as the definition of the trigonometric functions for complex arguments . For example, letting , we have:
In addition
Complex exponentials can simplify trigonometry, because they are mathematically easier to manipulate than their sine and cosine components. One technique is simply to convert sines and cosines into equivalent expressions in terms of exponentials sometimes called ''complex sinusoids''. After the manipulations, the simplified result is still real-valued. For example:
Another technique is to represent sines and cosines in terms of the real part of a complex expression and perform the manipulations on the complex expression. For example:
This formula is used for recursive generation of for integer values of and arbitrary (in radians).
Considering a parameter in equation above yields recursive formula for Chebyshev polynomials of the first kind.
Topological interpretation
In the language oftopology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, Euler's formula states that the imaginary exponential function is a ( surjective) morphism of topological group
In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures ...
s from the real line to the unit circle . In fact, this exhibits as a covering space
In topology, a covering or covering projection is a continuous function, map between topological spaces that, intuitively, Local property, locally acts like a Projection (mathematics), projection of multiple copies of a space onto itself. In par ...
of . Similarly, Euler's identity says that the kernel of this map is , where . These observations may be combined and summarized in the commutative diagram below:
Other applications
In differential equations, the function is often used to simplify solutions, even if the final answer is a real function involving sine and cosine. The reason for this is that the exponential function is the eigenfunction of the operation of differentiation. Inelectrical engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the l ...
, signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ...
, and similar fields, signals that vary periodically over time are often described as a combination of sinusoidal functions (see Fourier analysis), and these are more conveniently expressed as the sum of exponential functions with imaginary exponents, using Euler's formula. Also, phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.
In the four-dimensional space of quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s, there is a sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
of imaginary units. For any point on this sphere, and a real number, Euler's formula applies:
and the element is called a versor in quaternions. The set of all versors forms a 3-sphere in the 4-space.
Other special cases
The special cases that evaluate to units illustrate rotation around the complex unit circle: The special case at (where , one turn) yields . This is also argued to link five fundamental constants with three basic arithmetic operations, but, unlike Euler's identity, without rearranging the addends from the general case: An interpretation of the simplified form is that rotating by a full turn is an identity function.See also
*Complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
* Euler's identity
* Integration using Euler's formula
* History of Lorentz transformations
* List of topics named after Leonhard Euler
References
Further reading
* *External links
Elements of Algebra
{{Leonhard Euler Theorems in complex analysis Articles containing proofs Mathematical analysis E (mathematical constant) Trigonometry Leonhard Euler